BUSINESS BOOKS

例題

1.關鍵路線分析

問題陳述

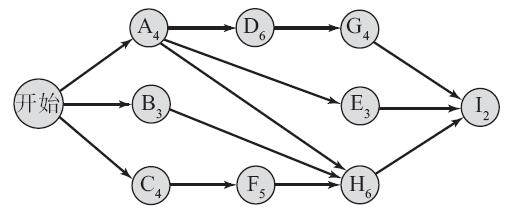
你帶領麥當勞的一個特殊的項目工作組，去執行一個叫作McWaffle的早餐項目。你已經準備好一份如下圖所示的網絡圖，其中有各種必要的活動和它們的期望執行日期。為每項活動計算進度時間ES、LS、EF、LF和緩衝時間TS。算出關鍵路線和項目工期。

解答

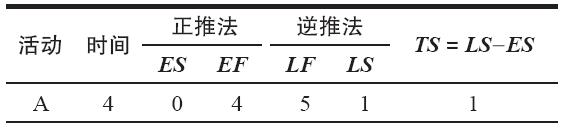
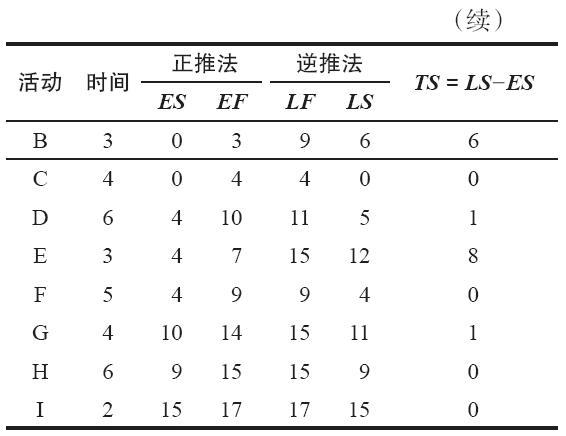
關鍵路線的活動是C、F、H和I，因為每項活動的TS=0。項目工期即關鍵路線上活動時間的總和是17天。

2.活動突擊

問題陳述

對於上面的網絡圖而言，假定一項活動每天以美元計算的趕工成本等於它的時間（如減少活動H的時間成本是1天6美元），再假定每項活動只能壓縮1天。應該突擊哪些活動，從而以最低的成本減少項目工期3天？

解答

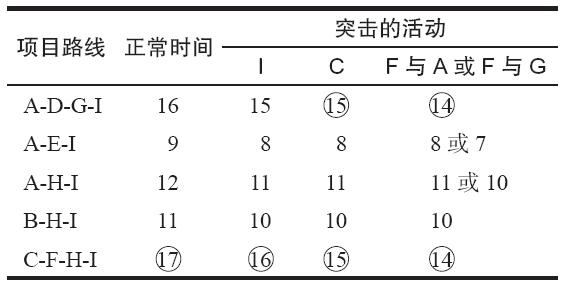
在下表中，圈起來的數字表示項目工期，從17天開始。當活動C被突擊後，兩條路線變得關鍵了，因此，必須突擊兩項活動（每條路線一項）來達到14天的項目工期。

3.在活動時間中加入不確定因素

問題陳述

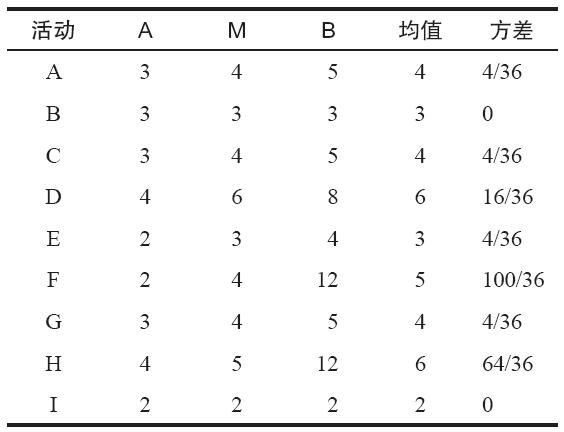
假定上面的McWaffle項目包含如下表所示的不確定活動時間。計算所有活動時間的均值和方差，並確定不突擊任何活動在20天內完成該項目的概率。

解答

首先，用式（16-8）和式（16-10）計算每項活動的均值和方差：

其次，確定關鍵路線。這項計算得出的活動的均值與原來問題中描述的活動均值相同。因此，關鍵路線是C-F-H-I，期望時間是17天。項目完成時間的方差是各項活動完成時間方差的總和。由此得出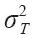=4/36+100/36+64/36+0=168/36=4.67。使用式（16-11），我們能算出20天內完成項目的Z值：

使用附錄A的標準正態分佈表，我們查到概率為0.5+0.4177=0.9177，或者說20天內完成項目的概率接近92%。