e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
15.7.1 期望值分析
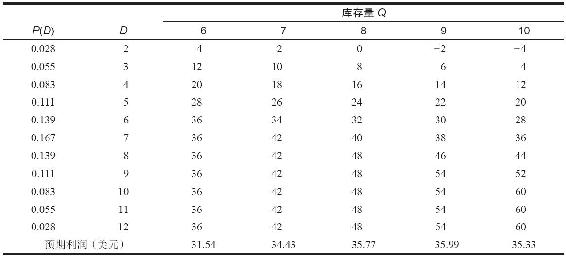
如表15-5所示,對於每一種盒裝甜甜圈的實際需求與選定庫存水平的組合,應列出結算表來闡明其利潤貢獻(為方便起見,我們將庫存水平Q的值限定在6~10之間)。將盒裝甜甜圈需求的概率代入,則結算表中每一列都可算出一個預期利潤。能夠產生最大預期利潤的庫存水平能夠最好地平衡喪失銷售時機的機會成本和滯存甜甜圈的投資成本。結算表最好從左上角開始構造。對於D=2,Q=6,從結算表中可得以下結果:

請注意,沿結算表中的每一行從左向右移動,利潤以(S-C)=2-4=-2美元遞減,這是因為每向右移動一格,滯存的甜甜圈就增加一份。沿結算表的每一列從上往下移動,利潤以(P-S)=10-2=8美元遞增,這是因為每向下移動一格,甜甜圈就多賣了一份。利潤持續增加直至在對角線上達到D=Q,再往下利潤將保持不變,因為所有庫存的甜甜圈已經都賣出去了,而多餘的需求也沒有能滿足。
對於從6至10的每一庫存水平Q,我們算出了它們的預期利潤並列於表的末行。例如,Q=6的預期利潤等於第一欄中的需求概率P(D)乘以第三欄中與Q=6相對應的各個結算數後取和。
當Q=6時的預期利潤=0.028×4+0.055×12+0.083×20+…+0.055×36+0.028×36=31.54(美元)
本例中,Q*=9時的利潤35.99美元為最大的預期利潤。
表15-5 結算表