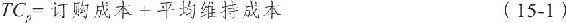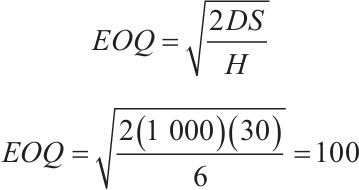e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
15.3.1 經濟訂購批量
這一簡單的“經濟訂購批量”模型(EOQ)假定需求率為定值且沒有庫存短缺,它應用在零售雜貨店所售物品(如糖、麵粉和其他農產品)上時出奇地精確。針對上述雜貨,需求量一般是固定的,因為許多顧客都定期地購買少量上述物品,因此這些必需品是不允許缺貨的。圖15-4以一年中Q/D的分隔作為循環週期(Q/D=訂購量/年需求量),對這一簡單模型中的庫存平衡進行了描述。
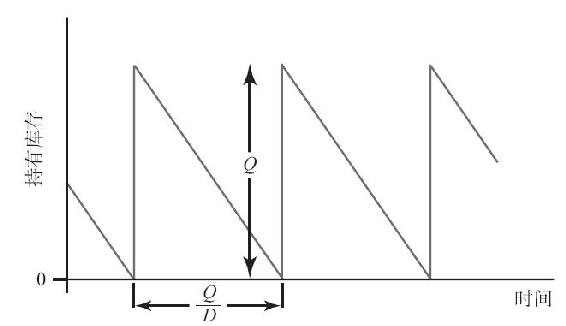
圖15-4 EOQ模型的庫存水平
例如,若Q為100,年需求量D為1200,則循環每月重複一次。我們要求的是Q*,即相關成本最低時的訂購量。這裡沒有缺貨成本是因為它們並未發生,並且我們排除了年購貨成本,因為我們假設單位成本是定值,所以訂貨數量的多少對購貨成本無影響。兩個增量成本(與訂購數量有關的成本)為訂購成本和維持成本。則一年期EOQ庫存系統的總購貨成本(TCp)為:
我們希望式(15-1)能夠更實用地加以表達。第一步,我們先來定義一些概念:
D——年需求量;
H——每單位庫存的年維持成本(用美元表示);
S——每次訂貨的訂購成本(用美元表示);
Q——訂貨量。
請注意,D和H必須以相同的時間單位計算(例如月或年)。
年訂購成本很容易得到。因為所有的需求量D必須滿足Q的訂購規模,那麼每年需要D/Q次訂貨。若每次訂購的成本為S,則年訂購成本為S(D/Q)。年庫存持有成本也可以直接求得。假如一單位的貨物儲存一年的持有成本為H美元,從圖15-4可知,最大的庫存平衡為Q,最小庫存平衡為零,則平均庫存水平為Q/2,所以得出年庫存維持成本為H(Q/2)。
則式(15-1)變為:
如圖15-5所示,維持成本和訂購成本隨Q值的不同而不同,且總成本曲線有最低點。因此,有一個特定的Q值對應庫存系統的最小年度總成本,這個值就是EOQ,但其鄰近的各Q值所對應的總成本也僅是略高而已。
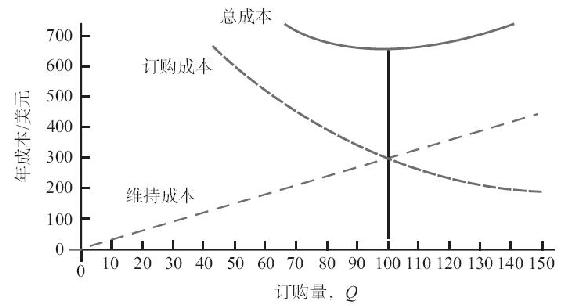
圖15-5 EOQ模型中的相關年成本
有好幾種方法可用來確定EOQ的值。例如,對式(15-2)的變量Q進行微分,設微分值為零,就可解得EOQ值。1另外一種更簡便的方法是:觀察到TCp最小時,維持成本與訂購成本相等,因此,令二者相等可解出EOQ。
⊙【例15-1】
落基山電力公司的EOQ
落基山電力公司(RMP)存儲的零配件的價值接近800萬美元。這些庫存由上千種不同的庫存單位(SKU)組成,它們的用途是發電和維持生產線的正常運轉。這些庫存平衡由計算機信息系統進行更新。
玻璃絕緣體(SKU1341)的消耗量基本維持穩定,每年平均消耗1000片。RMP以每片20美元的價格購進,並將它們運到丹佛的倉庫存儲起來。當庫存平衡達到預定的再訂貨點時進行補充訂貨。每次訂購的成本約為30美元,其中包括處理訂貨、接貨及擺貨的成本。
估計每片SKU1341的年庫存維持成本為6美元,這一維持成本包含30%的資金機會成本。SKU1341是一種關鍵原料,RMP必須避免它的庫存短缺。我們希望在使相關庫存成本最小的基礎上,決定每次SKU1341的訂貨量。
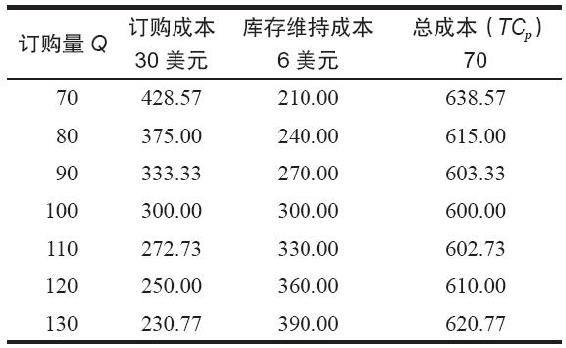
表15-2 庫存成本列表
從上文的敘述來看,得到已知條件:
D——每年1000片;
S——每次訂貨30美元;
H——每年每片維持成本為6美元。
將不同的Q值試代入式(15-2),看總成本的變化。如表15-2所示,當Q從70片開始增加時,TCp逐漸遞減,直到減至最小值600美元。從這一點開始,TCp又開始增加。由此可知此Q值即為EOQ,對應著總成本的最小值。據此畫出圖15-5,可見這些值形成了年度總成本的碗狀曲線。當然,我們也可以用式(15-3)直接求得EOQ:
如表15-2所示,當Q*=100片時,總成本600美元由訂購成本和維持成本平均分攤,各300美元。然而,Q=100的臨近值是更適合的。例如,訂購120片(10箱,每箱12片)的TCp,每年僅比EOQ多10美元。