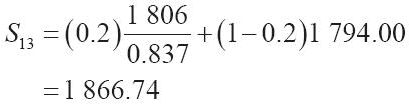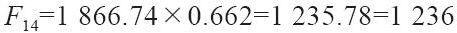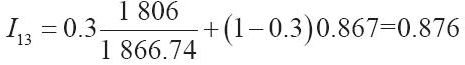e2 Sanjeev Bordoloi 服務管理：運作、戰略與信息技術 v9

14.5.6　考慮季節性調整的指數平滑法

我們用簡單指數平滑法的另一種擴展模型來說明一組數據的季節性影響。首先，我們用最簡單的方法剔除數據中的季節性，然後用所學知識將這些數據修勻，最後，重新加入季節性以做出預測。

表14-5中列出了2019～2020年每月乘渡船到加勒比一個島嶼旅遊的遊客數量，我們要對這些數據進行季節性調整。通常要設定一個週期L，作為一個季節的長度。L可以是任意時間長度，甚至是一天的24小時，但正如本例所示，L一般為12個月。值得注意的是，在開始用指數平滑法計算、預測之前，至少要有一個完整季節的實測值。

現引入季節指數It來剔除給定週期L的季節性影響，用t時期的真實值At除以週期L內所有時期的均值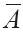，求出It：

式中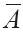，=(A1+A2+…AL)/L。

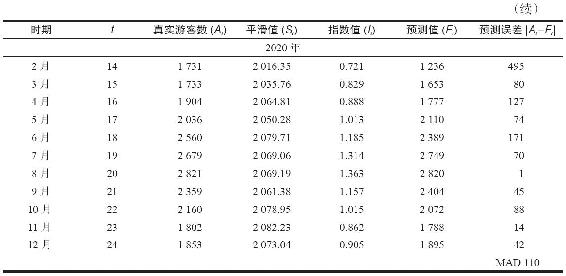
表14-5　考慮季節性調整的指數平滑法（乘渡船到島上的遊客數：α=0.2，γ=0.3）

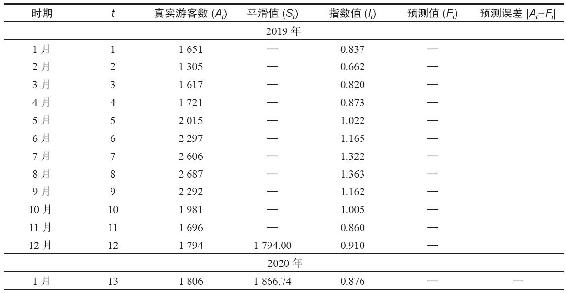
在本例中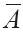，=1971.83（2019年每月平均乘客數量），將其代入式（14-13），求出第1個季度12個時期的指數It，在表14-5中第五欄內列出了2019年每月的指數值。然後按式（14-14），用這些數據剔除2020年各月中的季節性影響。式（14-14）是對式（14-5）做了微小變動得出的，即用指數It-L對At進行調整：

本例是用2019年12個月的數據對季節指數做最初的估計，因此，直到第13個時期（即2020年1月）才能計算出新的平滑值。在計算之初，假設S12=A12，即表14-5中的1794.00。用式（14-14），可以計算出2020年1月的平滑值，It-L=0.837（即12個月前的2019年1月的指數It），α=0.2：

對1月份的指數值進行季節分析來預測2月（t+1時期）的數值：

注意，季節係數It-L+1是2019年2月的指數It。因此，2020年2月的預測值為：

如果季節指數是穩定的，那麼只根據一個週期L做出的預測應該是可靠的。然而，如果指數不穩定，那麼就需要調整、修勻，新的數據也就可靠了。根據最近t時期的真實值At求出平滑值St，可以找到新的t時期季節指數（At/St）。將指數平滑的概念應用於指數中，我們引入一個新的常數γ，通常將其值定為0.1～0.5之間。季節指數的平滑估計可用下式求出：

現在，我們用式（14-16）來繼續表14-5中2020年的計算，求出最新的用於未來預測的每月季節指數。但是，應該認識到在實際操作中，L週期新季節的每一週期（即月）的平滑值、指數、預測值是基於最近期可靠的真實值逐月計算出來的。因此，按式（14-16），可求出2020年1月的新平滑季節指數I13（設γ=0.3）：

2020年2月至12月的MAD=110，這表明對表現出明確季節性的真實值做出了很好的預測。但是，是否有可能做出更精確的預測呢？