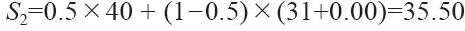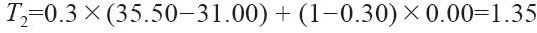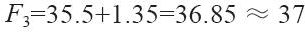e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
14.5.5 考慮趨勢調整的指數平滑法
一組數據的趨勢是指在過去一段時期,被觀測值從某一時期向另一時期變化的平均變化率。由趨勢引起的變化可以用簡單指數平滑法的擴展方法處理。
表14-4列出了一個往返於兩地間的航班前8周的運營情況,顯示出平均每週承載係數(即已售出座位的比例)在穩定上升,從第1周的大約30%升到第8周的70%左右。本例中,用式(14-10)計算出平滑值St。式(14-10)是在式(14-5)的基礎上變換而來的,它在原先的平滑值St-1中加入了趨勢值Tt-1以說明每週承載係數增長的變動率。
在計算中考慮趨勢調整時,我們用β作為平滑常數。該常數通常設定在0.1~0.5之間,可能與α相同,也可能不相同。(St-St-1)是給定t時期的趨勢,它描述的是從一個時期到另一個時期平滑值的變化率(即需求曲線的斜率)。用式(14-11)可以計算出t時期的平滑趨勢Tt,式(14-11)是式(14-5)經過變換得出的,即用實測趨勢(St-St-1)代替At。
為了預測業務啟動階段的現金流量,航班的經營者希望能預測出未來每週的承載係數。觀察了前兩週的情況後,就可以對第3周的情況進行預測。表14-4中的平滑值、趨勢值、預測值是分段計算出來的。因為第1周是這一系列預測中的第1個時期,所以其平滑值S1等於真實值A1,平滑趨勢T1=0.00。第2周的預測值是用式(14-12)計算得出的。本例中,F2=31+0.00=31.00。
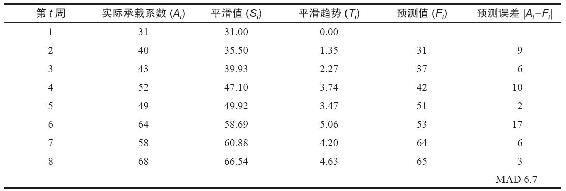
表14-4 考慮趨勢調整的指數平滑法(航班承載係數:α=0.5,β=0.3)
設定α=0.5,β=0.3來計算第2周的數值以及第3周的預測值。首先,用式(14-6)求出第2周的平滑值S2:
然後用式(14-7)求出第2周的趨勢值:
最後用式(14-8)求出第3周的預測值:
在得到以後各周的實際數據後,可以用相同的計算方法求出平滑值、趨勢值、預測值以及預測誤差。表14-4中列出了這些結果(MAD=6.7)。
預測誤差的和(不論正數、負數)測量的是預測偏差,在本例中,∑(At-Ft)=9+6+10-2+11-6+3=31。對於無偏預測來講,其預測誤差之和應該是接近於零(即正、負誤差可以互相抵消)。
圖14-3中分別畫出了實際承載係數和預測值。值得注意的是,除了第5周和第7周,經過趨勢調整的預測值都是滯後於真實值的。
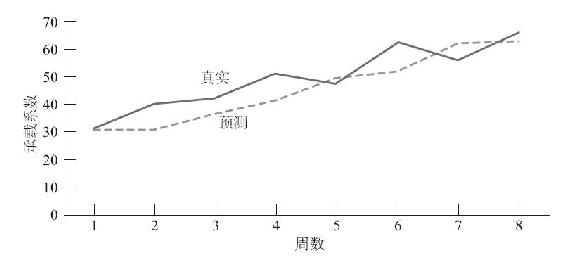
圖14-3 考慮趨勢調整的指數平滑法:航空公司的承載係數(α=0.5,β=0.3)