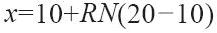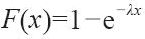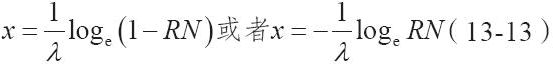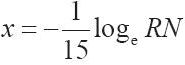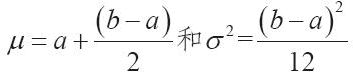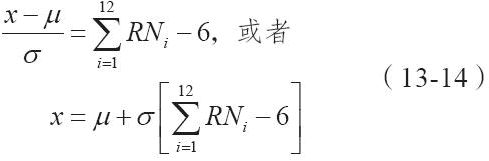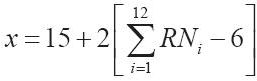BUSINESS BOOKS

附錄13A　計算機模擬

計算機模擬提供了一種研究真實系統的模型，以決定系統如何對政策、資源水平或顧客需求的變化進行響應。從我們的觀點來看，系統被定義為一組要素相互作用以實現目標的集合。系統模擬能用於回答關於現有的或計劃中的系統的“假設分析”問題。例如，如果為銀行增加一名出納員會怎麼樣？如果一些出納員只處理存款會怎麼樣？在大廳外面增加一臺ATM會怎麼樣？系統對於這些變化的響應能夠在長期內通過模擬的方法去發現。模擬模型不需要改變真實系統，就可以對每一個感興趣的場景形成系統績效的估計，例如平均顧客等待時間。在個人電腦上運行的靈活的模擬系統允許決策者根據時間變化觀察系統的活動（例如，顧客流動）。

從本質上說，服務交付系統不僅是動態的，而且是隨機的。動態的系統就是說它會受隨著時間變化的行動的影響。例如，在航空公司候機樓的排隊行為就受到每天不同時段的旅客到達的影響（例如，清早和中午）。隨機性是指系統服從概率分佈的隨機發生的事件這一潛在的可能特徵。回憶一下，顧客到達的泊松分佈就是一個隨機過程，因為即使在一個小時內的平均到達數是已知的，任何未來顧客的到達也都是不可預知的。表13-8列舉了一些將模擬應用於服務的例子。

表13-8　模擬在服務業中應用的實例

13A.1　系統模擬的流程

計算機模擬主要是一種評價新構想的工具。開發模擬系統的過程是一項艱鉅的任務，它可以通過使用像ServiceModel這樣的建模軟件來進行簡化。這種軟件將在以後討論。系統模擬的流程如圖13-7所示。

13A.1.1　模擬方法論

對問題進行精確而簡明的定義很重要，因為這個活動包括流程中的顧客並且促進結果的實現。目標的陳述自然會遵循並且為模型和系統績效評價的範圍提供框架。

為了節約時間，數據蒐集和模型開發通常同時完成。對於正在運行的系統，顧客到達時間分佈的歷史數據可能是可得的，數據也可以在現場蒐集。對於那些還不存在的系統，當然就沒有數據，但是也可能利用來自相似系統的其他數據。模型開發始於系統的抽象，可能是以流程圖的形式。當事件處理和事件之間的關係確定以後，概念模型就可以變為邏輯模型。

在初步模型建立以後，需要檢測和核對以確定其能否按照預計方式工作。通過一步步運行模型來完成檢驗，以確定其遵守了預計的邏輯。另一種方法是進行一些手工計算，看其是否與計算機輸出結果一致。大多數複雜的模型需要進行“調試”以修改其邏輯上的錯誤。

確認就是確定模型充分研究說明了問題的細節，反映了實際系統的運作。從真實系統蒐集來的數據可以與模型生成的結果相比較。例如，在一個救護車模型的確認中，就可以使用響應時間的歷史分佈來與模型預測的分佈相比較。確認階段也是極好的與顧客聯繫的機會，因為顧客對系統的熟悉和需要是對模型可信度的肯定。

然後，對被評估的可選項目使用最初的創意去進行模擬實驗。使用程序和檢測去分析和比較可選項目。需要控制對隨機要素的研究，通過指定能產生完全相同事件的共有的隨機數據流，確定每一個實驗都服從於相同的隨機性。對於模擬輸入的控制可以保證觀察到的結果完全歸因於“作業”，並沒有被環境中的變量影響。模型在一定數量的複製下運行，在穩態記錄統計數據以前，應先確定預備時間（瞬態）。模擬運行的結果經常會建議進行另外的實驗。在救護車研究的案例中，我們發現確認哪一家醫院接收病人相當重要。

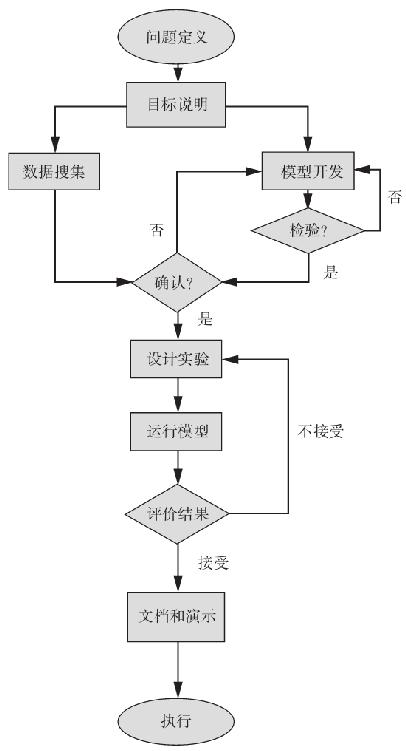
圖13-7　系統模擬的流程

模型的結構和相關的輸出結果應該記錄下來用作未來的參考。模擬軟件中的圖解能力提供了一種對於模型結果能夠自我說明的有效的可視化表述。

所實現的結果必須確保顧客從頭參與了整個模擬過程。最後，模擬研究結束後的分析能夠在下次項目中產生改進的創意。

13A.1.2　蒙特卡羅模擬

典型的系統模擬被用於分析那些無法使用分析方法實際解決的複雜模型。這些模型說明的真實系統通常是隨機的。蒙特卡羅模擬是一種允許我們使用其相關可能分佈區來模擬隨機變量的方法。

蒙特卡羅模擬依靠的是與隨機變量相關的可能分佈的抽樣值。隨機變量的值從適當的分佈中隨機挑選並用於模擬。在模擬過程中，對這些隨機變量要反覆觀測以模仿變量的行為。

有許多方法能夠用來從隨機變量的可能分佈中選取觀測值，但它們都是基於隨機數理論。隨機數（random number,RN）是一類專門的隨機變量，它在0～1之間均勻分佈。這就意味著所有在區間[0，1]內的值被挑選的可能性相同。

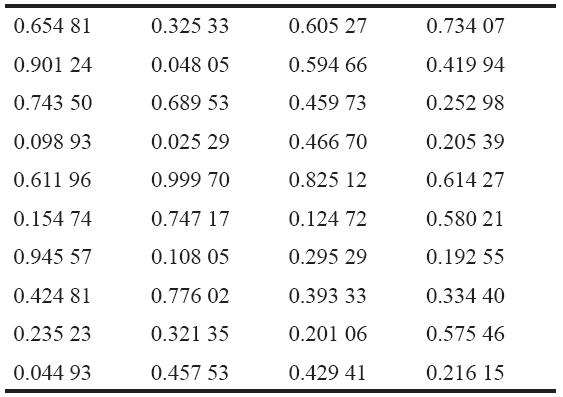
實際上，基於計算機的模擬使用的是偽隨機數。它們只是一些類似隨機數的值，儘管它們是使用數學函數生成的。雖然偽隨機數不是真正隨機的，但它們還是能表現出隨機性。偽隨機數有一個優點，那就是不需要佔用計算機大量的文件空間。更重要的是，通過使用從“種子”值而來的相同的數據流，它們可以實現實驗條件的精確複製。表13-9就給出了一些計算機生成的隨機數的樣本，使用Excel中的函數RAND()，返回一個均勻分佈在0～1之間的RN值。

表13-9　在[0，1]區間均勻分佈的隨機數

13A.1.3　生成隨機變量

怎樣使用隨機數去獲得隨機變量的觀察值呢？首先，我們需要明白隨機變量或者是離散的（例如，在一小時內到達的顧客數），或者是連續的（例如，對顧客進行服務的時間）。在這兩種情況下生成觀察值的過程都要使用任意隨機變量的唯一特徵——它的累積分佈和總是為1.0。

13A.1.4　離散隨機變量

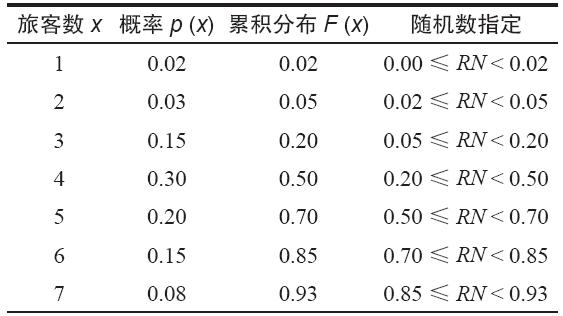
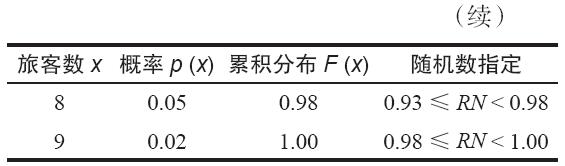
我們看一下，表13-10第1列顯示的是航空公司乘坐機場大巴的旅客的分佈。其第3列就表示了顧客數的累積分佈，它是由從上到下的概率的連續求和決定的[例如，F(2)=p(1)+p(2)=0.02+0.03=0.05]。累積分佈表示了這樣一種可能性，即旅客的數量小於或者等於某一特定值。概率必須在0～1的範圍內。回憶一下，隨機數是在區間[0，1]內均勻分佈的。累積分佈和隨機數RN之間的關係就是形成隨機變量觀察值的基礎。

表13-10　旅客數概率分佈和隨機數指定

現在我們就可以使用累積分佈和隨機數來形成搭乘機場大巴的旅客數的觀察值。這種形成隨機變量觀察值的方法非常簡明，被稱為“逆向轉換法”：

（1）從表13-9中任選一個隨機數。

（2）選擇與隨機數相應的累積分佈範圍。例如，在表13-10中，使用最後一列去尋找隨機數所在的區間。

（3）看第1列乘客的數量，它就是使累積分佈和隨機數相等的乘客數。這個值就是模擬中使用的觀察值。

看一個例子，從表13-9的左上角開始選擇第1個隨機數RN=0.65481。使用表13-10，可以看到0.50≤RN<0.70，這就與5個乘客相聯繫。這個過程在圖13-8中以圖形表現出來，在圖中使用柱形表示累積分佈。注意，每一個柱形在垂直方向的高度都等於相關隨機變量的概率。再進行一次觀察，我們從表13-9向下移動到下一個隨機數RN=0.90124。通過表13-10看到0.85≤RN<0.93，我們發現7個乘客就是第2個觀察值。如果多次重複這一過程，我們會發現，有2%的服務時間觀察值是1個乘客，3%的時間是2個乘客等，它模擬了真實的分佈。

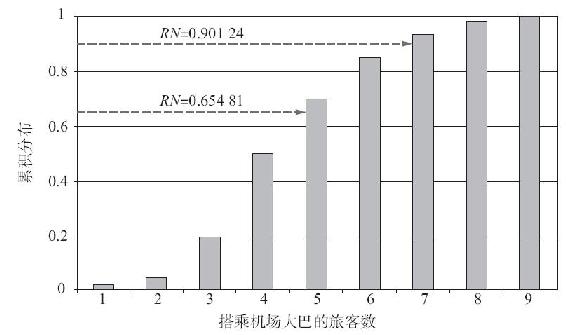
圖13-8　旅客數的累積分佈

13A.1.5　連續隨機變量

從一個連續分佈中選擇隨機變量的方法是使RN和累積分佈函數相等，並且得出隨機變量的值。我們通過三個常見的連續隨機變量分佈來說明這個方法：均勻分佈、負指數分佈和正態分佈。

（1）均勻分佈。一個隨機變量均勻分佈在a和b(b>a)之間，對於指定的RN，計算其返回值x的函數就是：

例如，假定從遠程停車站到機場終點站的定點公交車的行駛時間的分佈在10～20分鐘之間是均勻分佈。對於這個例子，我們的隨機變量函數就是：

（2）負指數分佈。回憶一下第12章中負指數分佈的累積分佈，由式（12-2）給出：

設RN=F(x)=1-e^-λx，求解得到e^-λx=1-RN。取以e為底的對數，解出x，我們可以得到以下公式。對於給定的RN，可以求出一個負指數分佈的隨機變量x。

例如，假設到達車站的乘客數服從每小時平均到達15人的泊松分佈。如果我們希望形成到達者間隔時間的分佈，負指數分佈就是合適的。因此，從隨機變量公式得到到達者之間間隔的時間，如果以小時計即為：

（3）正態分佈。因為正態分佈的累積概率並沒有一個接近的表達式，我們使用中心極限定理的性質去設計一種方法，以形成一個μ=0、σ²=1的標準正態偏差z。我們先考慮兩點。首先，回憶中心極限定理，任何均值的分佈都是正態分佈；其次，隨機數RN在0～1之間均勻分佈。對於一個在[a，b]區間的均勻分佈，均值和方差是：

因此隨機數RN的μ=1/2，σ²=1/12。為了形成一個均值為0而方差為1的標準正態分佈，我們簡單地將12個隨機數相加，再減去6，如下所示：

例如，班車的行駛時間是均值為15分鐘、標準差為2分鐘的正態分佈，那麼隨機變量函數就是：

13A.1.6　離散事件模擬

離散事件模擬表示一些發生在特定時間點的事件，如顧客的到達、服務的結束等。當一個事件發生時，系統的狀態就會改變。例如，一位顧客到達就會提高系統的顧客到達數，一位顧客離開（即服務結束）則會減少數量。計算機採用一種被稱為“模擬時鐘”的定時裝置來記錄每項事件的發生。在每個事件發生後，系統狀態的描述符就被記錄下來。

圖13-9表示了一個航空公司售票櫃檯的離散事件模擬流程圖。首先，使用逆向轉換方法，基於間隔到達時間分佈，形成下一位顧客的到達時間。模擬時鐘從零時開始，等於下一個按時間排序的事件的時間。如果下一事件是一位到達者，那麼這位顧客或者開始接受服務或者正在等候，這主要取決於服務檯的狀態。而如果下一事件是一位離開者（即服務結束），那麼或者另一位顧客接受服務，或者服務空閒，這主要取決於排隊的狀態。系統的狀態依據事件不斷更新，而時鐘時間和預先設定的最大時間相比較，如果時鐘時間大於或者等於最大時間，則描述系統的簡要統計數據就被計算和打印，模擬也就結束了。否則，時鐘就繼續等待下一事件。

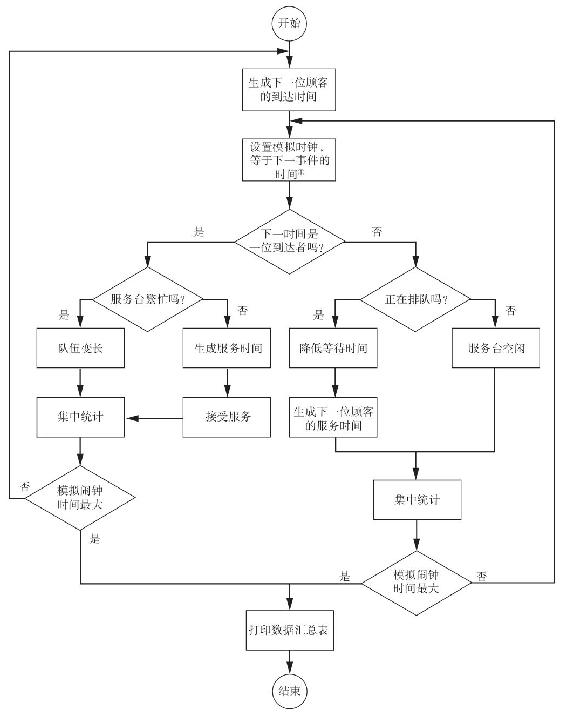
圖13-9　航空公司售票處離散事件模擬的流程

①下一事件是一位新顧客到達或者是當前顧客服務結束。

13A.2　利用ProModel進行過程模擬⁵

過程模擬器作為插件安裝在Microsoft Office Visio^®中，運行Visio過程流程圖、價值流圖和設施佈局內部的模擬模型，以此進行分析（如假定場景）、能力規劃（如測量增加額外的服務器對顧客等待時間的影響），或進行基本流程改進研究。免費試用版可在http://www.promodel.com/products/ProcessSimulator/處獲得，教程可在http://www.promodel.com/services/refreshercourse/上獲得。

⊙【例13-10】

航空公司售票櫃檯模擬

一個離散事件模擬系統被用於觀察航空公司售票櫃檯的活動。這個系統只有一個售票代理處，顧客按照先到先服務的原則接受服務。在模擬中，我們要考慮正在等待的顧客數、他們等待的時間以及售票處的狀態（即是忙還是空閒）。

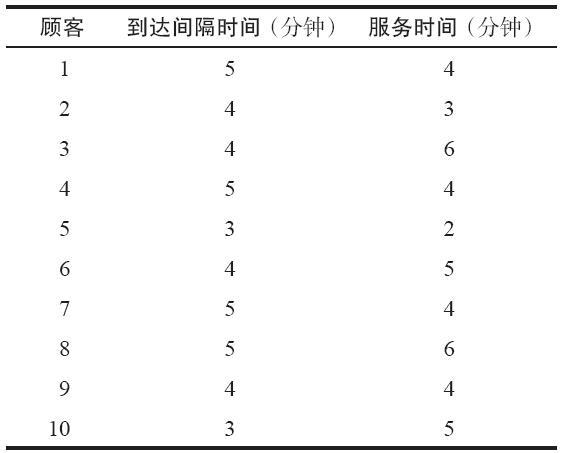
表13-11給出了服務時間和前10位顧客到達的間隔時間。服務時間和間隔時間使用逆向轉換法由適當的概率分佈得到。

表13-11　前10位顧客的到達間隔時間和服務時間

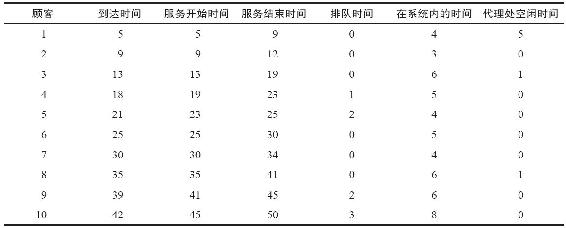
模擬時鐘從時間零開始。表13-12給出了每位顧客到達的時間、接受服務的時間以及離開的時間。例如，第1位顧客在時間5到達，馬上接受服務並在時間9離開。但是顧客4在時間18到達，發現服務忙。這位顧客在時間19接受了服務，而在時間23離開。10位顧客的總等待時間是8分鐘。這就得出每位顧客的平均等待時間是0.8分鐘。我們觀察到，售票處在總共50分鐘的時間內有7分鐘空閒，也就是14%的空閒率。

表13-12　前10位顧客的模擬（時間以分鐘計）

⊙【例13-11】

汽車駕照辦公室案例回顧

回顧第5章的案例5-2，其中我們開發了一個包括6個活動的流程圖，並將瓶頸活動標識為活動3“檢查違規記錄和限制條件”。這種靜態（例如固定的週期時間）的工作流分析方法沒有考慮到週期時間變化對系統績效的影響。排隊理論告訴我們，顧客到達時間和服務時間的變化會導致顧客排隊或閒置資源。下面重複使用表5-2中的數據，每個週期分配一個分佈。對於過程模擬器的應用示例，我們選擇了多種分佈：

·E(15)表示平均值為15的指數分佈

·U(30，5)表示平均值為30、半幅為5的均勻分佈

·N(60，5)表示平均值為60、標準差為5的正態分佈

·T(30，40，50)表示眾數為40、最小值為30和最大值為50的三角分佈

·給申請人拍照的時間是固定的20

·ER(30，2)表示平均值為30、形狀參數為2的愛爾朗分佈

圖13-10中的屏幕截圖顯示了使用屏幕左側可用的顧客實體圖進行駕照更新過程的流程圖。從顧客圖標到檢查申請書的正確性（第一個活動）的空箭頭是到達過程生成器，其屬性設置為E(60)，以對我們的模型進行壓力測試，因為平均每分鐘有一個到達者。每個活動都設置有與表13-13中相應的活動時間分佈的屬性。注意屏幕上方的過程模擬器（PROCESS SIMULATOR）。這個下拉菜單顯示了“模擬屬性”，其中設置了模擬練習的預熱時間、運行長度和重複次數。這個模擬的值分別為1小時、40小時和10次重複。

模擬報告如圖13-11所示。注意活動狀態的條形圖，運行所佔百分比顯示為純色，空閒所佔百分比顯示為條紋。這個圖清楚地顯示了“檢查違規記錄和限制條件”是瓶頸活動，在84%的時間裡都在運行。另外，請注意，顧客在系統中的平均時間是2240秒，這意味著顧客平均只在服務中花費大約9%(195/2240)的時間。

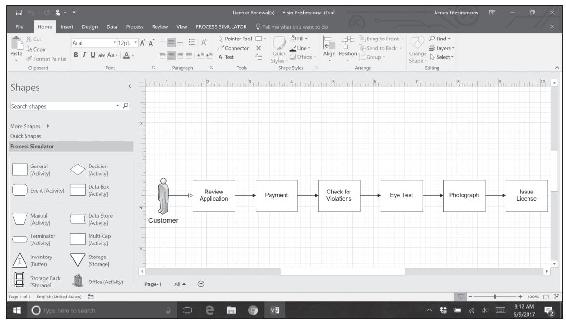
圖13-10　駕照更新過程流程圖的屏幕截圖

表13-13　駕照更新活動的時間分佈

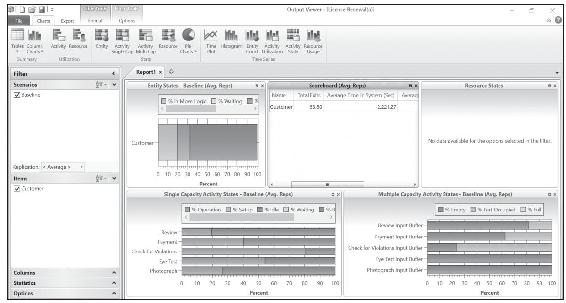
圖13-11　駕照更新過程模擬報告的屏幕截圖