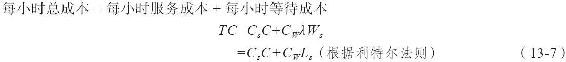BUSINESS BOOKS

13.4.3　顧客等待成本與服務成本之和最小化準則

如果顧客和服務檯都是同一個組織中的成員，那麼對於組織的有效性而言，提供服務的成本和員工等待接受服務的成本同等重要。員工等待時間的成本至少等於他們的平均工資；而且實際上，如果將等待的所有潛在成本都考慮在內，例如沒有完成工作的挫敗感或者工作拖延對組織中其他成員造成的影響，那麼，這個成本還會高得多。

圖13-1充分表明當可以通過增加服務檯的數目來提高服務能力時，組織決策者必須做出權衡。隨著服務檯數目的增加，服務成本上升，但是，它可以被等待成本的相應下降而抵消。兩項成本相加，即可得到該組織的一條呈凸形的總成本曲線，由此可以確定使總成本最小的最佳服務能力。利用排隊模型預測不同能力水平下的員工預期等待時間，將其值代入這裡的總成本函數。

假設服務和等待的線性成本函數以及不同方案之間的比較都是以穩定狀態下的系統績效為基礎，我們可以計算每單位時間（小時）的總成本，如下：

式中　C——服務檯的數目；

C_s——每個服務檯每小時的成本；

C_W——顧客等待的每小時成本。

在式（13-7）中，等待是指在系統中的逗留時間。但是，如果在某些情況下采用排隊等待時間更為合理，就應當用L_q代替L_s。當服務是自助形式時，例如使用複印機或傳真機，採用排隊等待時間或許是合理的。

⊙【例13-8】

工作站租入

一個規模很大的工程部門的經理正在考慮是否應該租幾個工作站，以便使所有員工都能夠分析結構設計問題。根據對員工們進行的調查，經理髮現該部門平均每小時就結構分析提出8個服務請求。據工程師估計，每一項分析平均需要15分鐘。如果只租用一個工作站來滿足所有這些需求，所需的租金是每小時10美元。當考慮工程技術人員的平均收入時，保留一名空閒工程師的成本為每小時30美元。經過快速粗略分析，經理假定服務請求服從泊松分佈，使用工作站的時間服從指數分佈。此外，這是一個足夠大的工程部門，可視為一個無限需求群體。利用標準M/M/c模型，其中ρ=8/4=2，由附錄C可以計算出L_q，經理得到的結果如表13-6所示。

表13-6　工作站租入各備選方案的總成本

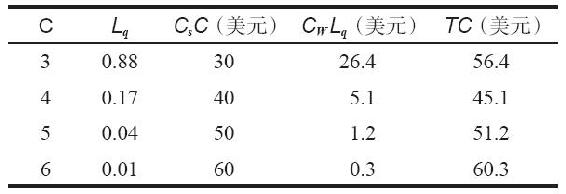
注意，由於工作站是生產性服務設施，所以這些計算公式中都用L_q代替L_s。結果表明，若使工作站租金加上等待服務的工程師工資這一總成本最小，應當租4個工作站。

如式（13-7）所示，我們假設等待成本是時間的線性函數。但是，這個假設是值得懷疑的，因為隨著拖延時間變長，很大一部分顧客會感到不滿意、大聲抱怨，很多人可能離去。首先，等待的時間越長，顧客就會變得越發不滿，他們以後到其他地方尋求服務的概率也就越大；其次，他們會向其朋友和親屬們描述這次不愉快的經歷，這也會對未來的銷售收入造成影響；最後，相比較而言，一次銷售損失是微不足道的，而永遠地失去一位顧客所造成的未來收入的損失卻是巨大的。然而在實踐中，人們還是經常採用線性假設，因為很難確定顧客等待成本函數。