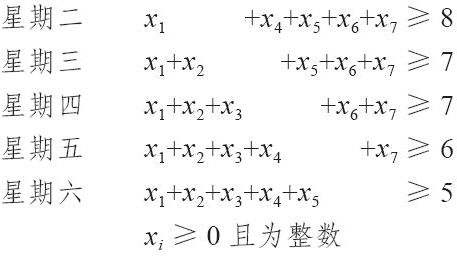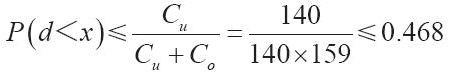BUSINESS BOOKS

例題

1.超額預訂問題

問題陳述

一個家庭旅館正在考慮使用超額預訂，因為預訂了而顧客又未出現的情況使得每年夏季很多房間閒置，如右表所示。一間空房的平均機會成本是69美元。然而，安排一個超額預訂的客人的成本是昂貴的，因為附近的度假勝地的客房價格平均為119美元，小旅館必須要填補這個差額。那麼，從超額預訂中每晚獲得的期望收益是多少？

解答

第一，用69美元作為空房的成本，用119-69=50美元作為推掉一位客人的成本，由此構造一個超額預訂的損失表。

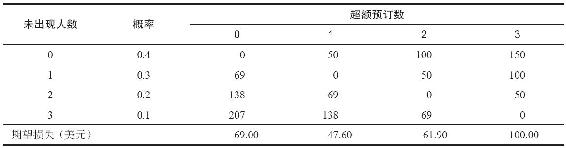
第二，將超額預訂每一欄與其對應的預訂而未出現的人數的概率相乘，然後將這些乘積相加，計算出期望損失。對於完全沒有超額預訂的情況，可計算出：

0×0.4+69×0.3+138×0.2+207×0.1=69

從期望損失行可以看到，超額訂購數為1時，期望損失最小，每晚從超額預訂中獲期望收益為69.00-47.60=21.40美元。

2.每週工作班次安排

問題陳述

一家大型租車公司的電話預訂部門對接線員每天要求的數量如下：

請提供一份有連續兩天休息日的班次時間表。

解答

把問題轉化為整數線性規劃模型，用Excel Solver來解。

目標函數：

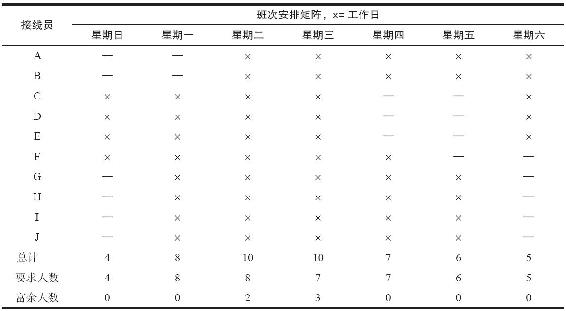
用Excel Solver解得：x₁=2，x₂=0，x₃=0，x₄=0，x₅=3，x₆=1，x₇=4。相應的周班制時間表如下：

3.收益管理

問題陳述

一個滑雪勝地正在計劃一項年底促銷活動，對週末的雙人間提供優惠的價格，每人159美元。在旺季，這些房間（包括纜車票）的價格通常為299美元。管理者想為未預訂上門的、打算付全價的遊客保留一些房間。如果打算付全價的滑雪者的比例大約是20%，他們的平均週末需求為正態分佈，均值為50，標準差為10。那麼要為這些付全價的滑雪者留出多少客房？

解答

使用式（11-1），我們可以確定臨界分位點如下：

查附錄A中的正態分佈表，累積概率0.468的z值為0.02。這樣，保留房間數為：

μ+zσ=50-0.08×10=49(間)