e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
11.4.3 休息時間有限制的每週工作班次計劃
正如前面指出的,制定班次以適應每日需求僅僅是問題的一部分。許多公共服務組織,例如警察局、消防局和醫院的緊急護理部門,都必須在一週的每一天和每天24小時隨時提供服務。對於這些組織來說,典型的員工每週工作5天、連續休息2天,但是不一定是星期六和星期日休息。管理人員對制訂工作計劃和滿足員工對工作日和週末安排的不同要求很有興趣。這個問題可以用一個整數線性規劃模型(integer linear programming,ILP)來準確表述。首先,要決定一週內每天需要的員工人數。這樣,此問題就變成了一個使那些分配到7個可能的班次中的員工人數最少的問題。每個班次包含5個工作日和2個連續的休息日,不同的班次在一週內的不同日期開始工作,但工作日都持續5天。可以利用整數線性規劃模型作為這個問題的通用公式。
變量定義:
xi——分配到班次i中的員工數量,這裡第i天是兩個連續休息日的開始(例如,分配到第1組的員工在星期日和星期一休息)
bj——第j天所需的員工人數
目標函數:
⊙【例11-3】
醫院急診室
醫院急診室的運營時間是每週7天、每天24小時。每個工作日被分為3個班次,每班8小時。白班需要的護士總數為:

急症室主任對制定一份工作安排以使所需的護士人數最少很有興趣。護士們每週工作5天,連續休息2天。在上述整數線性規劃模型的右邊輸入正確的限制條件(即b1=3,b2=6,…,b6=5,b7=5),用此方法得出:x1=1,x2=1,x3=2,x4=0,x5=3,x6=0,x7=1。這意味著有一個人在星期日和星期一休息,一個人在星期一和星期二休息,兩個人在星期二和星期三休息,三個人在星期四和星期五休息,一個人在星期六和星期日休息。表11-8顯示了相應的人員安排,只有在星期六和星期日出現了人員多餘的情況。
表11-8 每週護士工作安排表
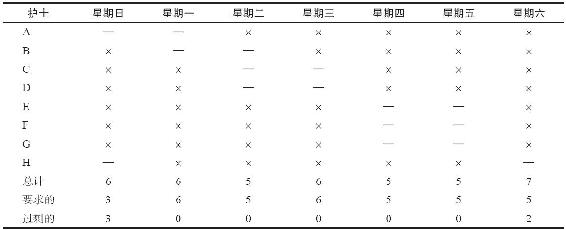
這些人員安排問題常常有多個最優解。例如,在這個例子中,解x1=1,x2=1,x3=1,x4=1,x5=1,x6=1,x7=2也是可行的,且所需的護士總數也是8人。為什麼第二組解可能比表11-8顯示的第一種方案更好呢?
