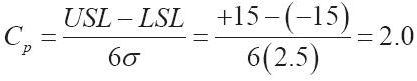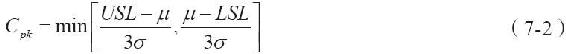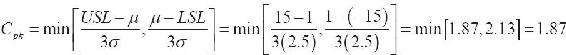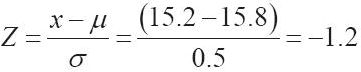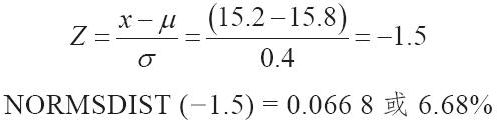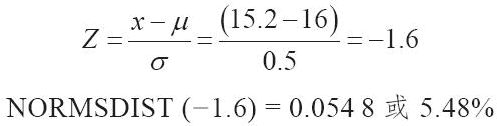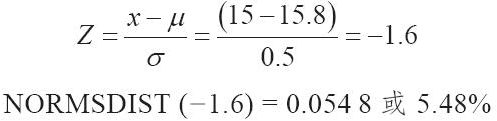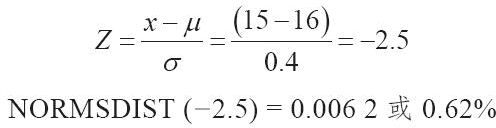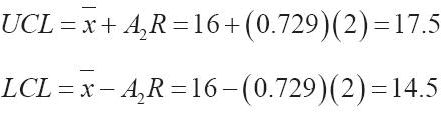e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
7.5.3 六西格瑪
20世紀80年代中期,摩托羅拉的工程師想通過強調質量問題來推動過程改善,從而決定每百萬產出中的不合格品的水平。摩托羅拉採用了這種標準,並實施了一種稱為“六西格瑪”的方法,由最高管理層在組織內部創造一種文化變革。這些努力的結果是,根據摩托羅拉的文件記錄,當時節省了160億美元,使成本直接降至底線,這和從均衡增加的收入中減去產品成本不同。這個財務表現並沒有被忽視,世界上許多公司採用六西格瑪作為一種經營方式。例如,有這樣一個傳聞,聯合信號公司(現在的霍尼韋爾公司)的拉里·博西迪(Larry Bossidy)和通用電氣公司的傑克·韋爾奇(Jack Welch)在一起打高爾夫,傑克和拉里打賭,他會在通用電氣公司比拉里在聯合信號公司更快地實施六西格瑪,並且能取得更好的效果。結果,通用電氣公司的財務結果遠遠超過預期,六西格瑪變成傑克·韋爾奇傳奇的奠基石。隨著時間的流逝,六西格瑪變得不再只是一個質量體系,而成為一種經營方式,它被視為一種願景、一種哲學、一個標誌、一個度量標準、一個目標和一種方法論。
變化是任何過程的一部分——從圖7-10的航空公司準時到達的圖形分析中可以看出這一點。組織經常用平均值來形容它們的努力,比如平均的循環時間,但是這樣做會由於忽略了變化而隱藏了問題。六西格瑪的目的在於在一定程度上減少或縮小績效上的變化,使得六項標準差能夠被擠壓進顧客規定的限制條件內。這些限制被定義為一個規格上限(USL)和一個規格下限(LSL)。圖7-10顯示出,通常的偏離大大超出了顧客對規定起飛或到達時間正負15分鐘的偏離期望值。當過程去除了足夠的偏離時,六西格瑪的目的就實現了,於是正負15分鐘的範圍就會跨越正負六個標準差(σ)的目標分佈區。
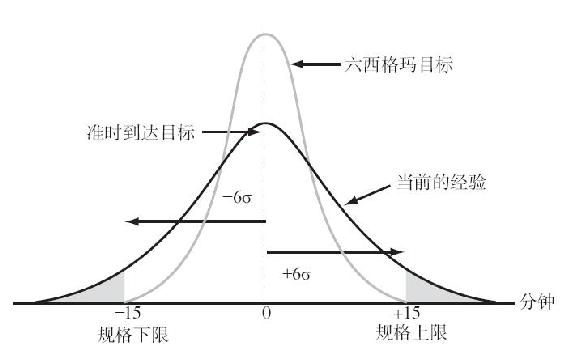
圖7-10 準時到達的分佈狀況
努力減少可變性需要一種關於達到規格目標的過程衡量方法。過程能力指數是在實現目標的過程中,計算有多少過程變化被減少的一種統計方法。當均值只集中在規格限定的範圍內時,使用過程能力指數Cp:
對於六西格瑪標準,Cp≥2.0被認為是可以接受的過程能力指數。以圖7-10準時到達的分佈圖為例,我們可以看到,σ=15/6=2.5是滿足六西格瑪目標變化的最低水平。
當均值沒有集中在規格限定的範圍內時,使用過程能力指數Cpk:
回到圖7-10,讓我們假設準時到達的均值的變化範圍從μ=0到μ=+1,標準偏差σ仍然是2.5。
除非增加USL的值到16,以反映一個新的平均值,否則我們將沒有一個過程能夠滿足Cpk≥2.0的六西格瑪的期望值。
六西格瑪是一個嚴格的經過訓練的方法論,它使用數據和統計分析的方法來測量和改進公司的經營績效,識別和改正缺陷以加強顧客滿意度。六西格瑪要求一個組織具有這樣的組織文化:組織中各個層次的員工都有持續改進的願望,其最終目的是獲得每100萬顧客中只有3.4個錯誤出現的實質性的完美結果。在統計學中,如果假設一個過程變量是正態分佈,那麼六個標準差在分佈的尾部定義了一個0.0000034的概率。六西格瑪的重點在於報告錯誤,這比評價績效成功的百分比更加具有激勵性。例如,一家隔夜送達的快遞公司,如聯邦快遞,可能為99.9%的遞送準確性而自豪。然而,如果它一天內送100萬個包裹,那麼將有1000個送錯!有趣的是,其中1/2的錯誤是由於顧客的誤導造成的,除非顧客的投入是正確的,否則六西格瑪的目標永遠也不能達到——這是服務質量的一個傳統問題。
六西格瑪是項目導向的,強調自上而下的支持和領導,以識別機會從而使財務效益最大化。六西格瑪項目的目標是減少缺陷(服務失敗)、成本、工藝過程的變化,提高生產力,提高顧客滿意度。六西格瑪項目的責任是通過一個有層次的培訓和職責的分配構建的。圖7-11給出了角色,並按照主管人員、監督執行負責人、黑帶大師、黑帶、綠帶和項目成員這個層級順序分配職責。鼓勵技能提高,例如項目成員可以通過培訓提升為綠帶,再到承擔組織六西格瑪項目這一更高層級的職責。如表7-3所示,六西格瑪使用DMAIC(定義、測量、分析、改進、控制)循環結構(如例7-1所示),努力改善那些執行得未達到期望的現有流程。
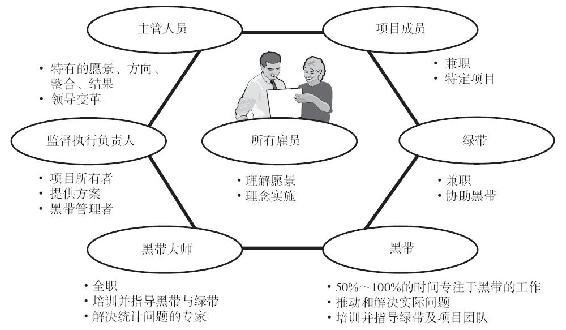
圖7-11 六西格瑪的組織角色和職責
表7-3 六西格瑪DMAIC的過程步驟

⊙例7-1
大特克斯漢堡(Big Tex Burgers)
大特克斯漢堡是一家以其巨型漢堡而聞名的快餐連鎖店。最近,一家顧客組織批評該餐廳,聲稱其漢堡包含的肉餅少於16盎司[1]。你是餐廳的質量保證經理,老闆要求你調查此事。這是你閃光的機會,因此你決定使用六西格瑪的DMAIC步驟來評估情況。
步驟1:定義
肉餅的重量是肉餅的關鍵質量特性。
步驟2:測量
為了評估問題的嚴重程度,我們首先需要為漢堡的質量特性(肉餅的重量)設定可接受的限制。因此,將質量限制設置為廣告中所說的重量的±5%。
容許上限=16+(0.05)(16)=16.8
容許下限=16-(0.05)(16)=15.2
接下來要回答的問題是,漢堡中肉含量低於15.2盎司的比例是多少。請注意,即使顧客可能不反對在漢堡中攝入超過16.8盎司的肉類(即高於容許上限),但你必須將其視為內部錯誤,因為它會影響利潤。
步驟3:分析
接下來,隨機採集漢堡樣品並稱重。你發現樣品的平均值為15.8盎司,標準偏差為0.5盎司。即使15.8盎司的平均重量低於16盎司的廣告重量,我們也不能自動暗示錯誤是顯著的,並將系統視為“有缺陷”。要將系統歸類為有缺陷,你需要確定是否有很大比例的漢堡包低於15.2盎司的可接受限度。
使用標準正態分佈,
使用附錄A中的標準正態分佈表,或使用Excel命令,我們發現負尾區域為:
NORMSDIST(Z)=NORMSDIST(-1.2)=0.1151
現在,你可以推斷出11.51%的漢堡重量可能少於15.2盎司。
步驟4:改進
你的老闆認為11.51%的不良率是不可接受的,公司的業績需要提高。你確定了三種實現所需改進的方法:①減少偏差;②調整16盎司的基準;③提升規格。
首先,假設通過工藝改進,標準偏差可以從0.5盎司減少到0.4盎司。於是,
或者,當前標準偏差為0.5盎司時,假設過程可以調整(居中),使新的平均值正好為16盎司。於是,
第三種可能性是與顧客組織協商,將可接受的範圍擴大到15~17盎司之間。於是,
因此,你發現使用三個選項中的任何一個,“缺陷”率都可以從當前的11.51%降低到5%~7%的範圍。如果所有三個選項同時使用,則,
這一共同努力使只有不到1%的漢堡包超出可接受的下限。
步驟5:控制
在獲得所需的改進之後,必須持續地控制質量標準。回顧第6章“服務質量”中的內容,使用控制圖可以實現過程的統計質量控制。因為你對控制漢堡的重量感興趣,所以使用圖x和R圖是合適的。你決定構建一個控制圖,預期重量x為16盎司,預期範圍R為2盎司。每小時抽取4個漢堡,計算平均值和範圍。根據第6章中的表6-7,樣本量為4,我們發現A2=0.729,D3=0,D4=2.282。使用第6章中的公式(6-1)和(6-2),可以發現範圍的控制極限為:
使用第6章中的公式(6-3)和(6-4),你可以發現樣本平均值的控制極限是:
由於你的工作,大特克斯漢堡將實施每小時隨機抽樣4個漢堡的做法,記錄重量範圍,並計算平均值。該信息將記錄在兩個單獨的圖表上,範圍圖表和重量圖表,其中繪製了UCL和LCL線。超出這些控制限值的記錄值說明應採取措施找出重量控制損失的根本原因。
[1] 1盎司=28.350克。