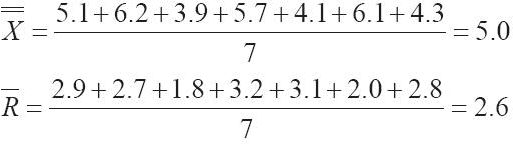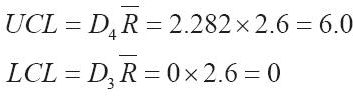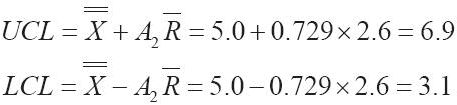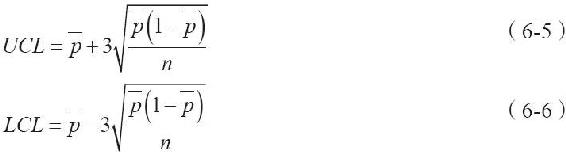BUSINESS BOOKS

6.5.2　統計過程控制

服務績效常通過關鍵指標來判斷。例如，一所高中的教育質量可以通過學生的教育能力測試（SAT）得分來衡量；警察局遏制犯罪計劃的有效性可通過犯罪率來確認；銀行出納員的工作績效可以通過每天結賬的準確性來判斷。

當服務過程的績效達不到預期水平時應該怎麼辦？通常來講，需要開展調研以識別問題的原因並提供糾正方案。但是，績效的變化可能是由隨機事件引起的，或沒有明確原因。決策者要探明服務質量下降的真正原因並避免與不良服務相關的成本損失。另一方面，應儘量避免對良好系統做不必要的改動。如表6-5中顯示的那樣，在控制質量中有兩類風險。這些風險根據受損害一方來命名。如果系統運行正常而被認為失控時，這時發生Ⅰ類錯誤，即生產者風險；如果系統運行不正常而被認為正常，這時發生Ⅱ類錯誤，即顧客風險。

表6-5　質量控制決策風險

統計過程控制是使用控制圖來監控過程性能測量，該測量指示何時需要干預。稱為“控制圖”的視覺顯示用於繪製性能測量值（例如，救護車響應時間）隨時間的平均值變化，以確定過程是否保持在控制中（即，性能均值和方差未改變）。圖6-9中顯示了用於監控救護車反應時間的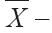控制圖。這是日常繪製的平均反應時間圖，可以用來監控那些不正常的與標準偏離的情況。當測量值落於控制限外，高於控制上限（UCL）或低於控制下限（LCL）時，就認為過程失控了。這時，需要關注系統。以急救為例，前7天所有觀測均值都呈現預期值，處於控制內，而到了第10天，觀察值超出了UCL，是不太正常的現象，需要進行根源分析。

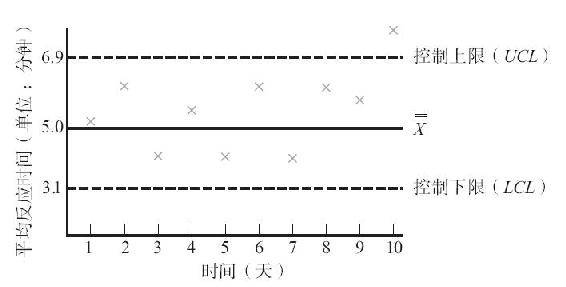
圖6-9　救護車反應時間圖

構建控制圖與確定樣本平均值的置信區間相似。回憶一下統計學，根據中心極限定理，樣本平均值趨向正態分佈（雖然統計量的分佈可以是任何形式的，但其平均值服從於正態分佈）。我們從標準正態分佈表中可知，正態分佈的99.7%落在3倍標準差之內。使用具有代表性的歷史數據可以確定一些系統績效的平均值和標準差。這些參數被用來構建績效測量平均值的99.7%的置信區間。我們希望，將來隨機蒐集的樣本均值落在這個置信區間內。如果沒有落在這個區間，我們可斷言，過程變化了，真實的平均值移動了。

構建和使用質量控制圖的步驟概述如下：

（1）決定服務系統績效的測量方法。

（2）蒐集有代表性的歷史數據來計算總體平均值、系統績效測量方差。

（3）決定樣本大小，使用總體平均值和方差計算3倍標準差的控制限。

（4）將控制圖繪製成樣本平均值時間的函數。

（5）標出隨機蒐集的樣本平均值，並按下列方式說明結果：

1）過程在控制中（樣本平均值落於控制限內）。

2）過程失控（樣本平均值落於控制限外或連續7個點落於平均值一側），此時：

①評估現狀；

②採取矯正措施；

③檢查行動結果。

（6）定期更新控制圖，並且加入最新數據。

根據績效測量方式的種類將控制圖分為兩類。變量控制圖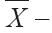（圖和R-圖），如案例6-2所示，記錄允許測量值為小數，如長度、寬度和時間。控制圖（p-圖）的特徵是記錄離散的數據，如缺陷數和以百分比表示的錯誤數，如案例6-3所示。

⊙例6-2

變量控制圖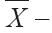（圖和R-圖）

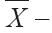圖的目的是發現一種連續變量在流程平均值中的變化（例如救護車的響應時間）。用於連續變量的R-圖測量流程的離散程度。表6-6包括了一輛救護車具有代表性的7天的反應時間的歷史數據。四次電話應答會在任何一天的任意時間發起，可能在早班、中班、晚班和夜晚的任一班。每一天的平均應答（依據4個觀察樣本）和範圍（即最高值和最低值之差）被計算出來並列在最後兩列。

預計應答均值和範圍計算如下：

R-圖常在確定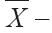圖之前建立以確保流程變化處在控制中。用於範圍的控制圖可以通過以下公式建立：

式中，R表示總體全距；D₄表示從表6-7中根據樣本大小n查得的UCL值；D₃表示從表6-7中根據樣本大小n查得的LCL值。

表6-6　救護車的響應時間（分鐘）

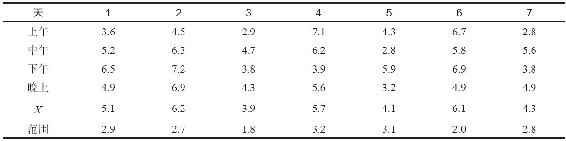
在救護車案例中，使用表6-7中的數據計算樣本數為4的全距控制限：

由於在表6-6最後一列的所有範圍值落入R-圖的7天UCL和LCL區間，因此流程的變化性得到了控制，並且我們能夠開始創建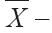圖。

用於計算控制極限的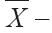圖的恰當公式，用表6-7中的A₂和R作為控制流程離散的測量。

對4個樣本的控制極限計算如下：

圖6-9顯示了救護車響應時間的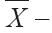圖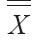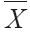，（平均值）=5.0，UCL=6.9，LCL=3.1。表6-6中前7天的樣品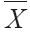平均值在表中列出，明確地描述了本週的表現，以在開始使用控制圖之前，明確該流程是受到控制的。從前7天中可以看出，所有的觀察結果落入UCL和LCL區間，因為該流程得到了控制。但在第10天，樣品平均值超過了UCL。因此，系統需要給予關注。假定我們的救護車樣本代表了佛羅里達羅德岱堡市的數據，春假時早上8點開始上班，則延長的海灘遊能夠解釋較長的應答時間。救護車春假期間在海灘的重新定位也許可以改進其表現。

表6-7　變量控制圖常數

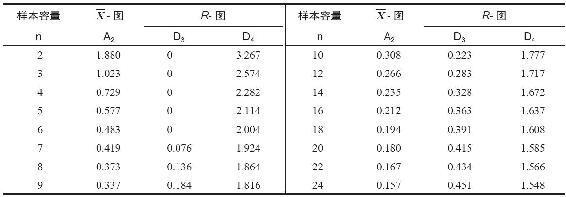
資料來源：引自費城美國測試與材料協會1976年版ASTM Manual on Presentation of Data and Control Chart Analysis的表27。

⊙例6-3

特性控制圖（p-圖）

在有些情況下，系統績效被劃分為“好”或“壞”，但重要的是較差績效的百分比。例如，郵局中一個機械化分揀設備的操作員必須讀包裹上的郵政編碼，根據這個編碼在城市中的位置，用傳送帶將包裹送到合適路線的卡車上。根據以往記錄，熟練操作員的出錯率約是5%，用小數表示為0.05。管理者想設計一個控制圖來監控操作員，以確定不能勝任的人。使用式（6-5）和式（6-6）來構建百分比圖（p-圖）。應熟悉以下這些公式，因為它們代表百分比圖的±3個標準差的置信區間。

式中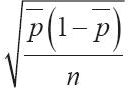，表示百分比標準差；p為總體百分比；n表示樣本數。

用式（6-5）和式（6-6）並從發運卡車中隨機抽取100個包裹樣本，計算分揀員的p-圖控制限。注意，如果計算出的控制下限是負數，將LCL取0。

圖6-10表示這位分揀員的p-圖。已知這個新人有9天試用經歷，你能判斷這個人適合分揀工作嗎？

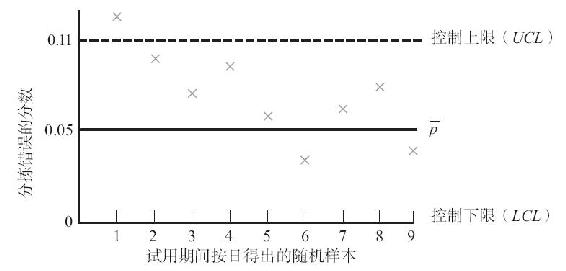
圖6-10　分揀員p-圖