e5 黄達 金融學 v3
第三節 資產定價模型
為什麼要研究資產定價模型
上一節,在討論有價證券價值確定的內容中,僅提示,應選取與風險相匹配的貼現率r。當學習了風險衡量以及資產組合的理論以後,就可以著手解決這一課題。
資產定價模型(asset pricing model),就是幫助我們找到適當的貼現率並確定資產價值的一種有用工具。
資產定價模型主要是資本資產定價模型(capital asset pricing model,CAPM)。後來有多要素模型和套利定價模型之類的發展。
資本市場理論
資本資產定價模型是1964年由威廉·夏普(William Sharp)、約翰·林特納(John Lintner)和簡·莫辛(Jan Mossin)三個人同時提出來的。這個模型以及有關的資本市場理論,是建立在馬科維茨奠定的資產組合理論基礎上的。
瞭解資本資產定價模型,首先需要了解資本市場理論。
在資產組合理論中,我們假設構造的組合中所有資產都是風險資產。如果引入無風險資產(risk-free assets)進入資產組合,資產組合理論作了這樣的假設:在資產組合中引入無風險資產,並且假定投資者對於風險資產的投資是按照一個特定的市場組合進行的,則新構成的組合包含一種無風險資產和一組風險資產組合構成的特定組合。無風險資產,在一個經濟體中基本只有一類,如政府債券。一組風險資產組合中的風險資產,在這裡並非包括任何種類的風險資產,而實際只是限定在證券市場上的風險資產,如股票。採取這種處理方法也有一定道理。因為股票價格的變化反映發行人的風險以及發行人所在行業、所在社會的風險;而股票市場則匯聚了來自多行業的眾多企業的股票。所以,股票市場所有資產的組合,在一定意義上可以代表社會所有風險資產的集合。這樣的風險資產組合稱為市場組合(market portfolio)。
用F和M分別代表一種無風險資產和市場組合,則新的資產組合等於F+M。這個新資產組合的收益和風險可根據公式(23·4)和公式(23·5)展開:


這是邁向資本資產定價模型的重要一步。
根據新資產組合的期望收益率和風險,可以在座標圖上劃出一條向上傾斜的、與馬科維茨資產組合曲線相切的直線。這條直線叫做資本市場線(capital market line),見圖23—3。
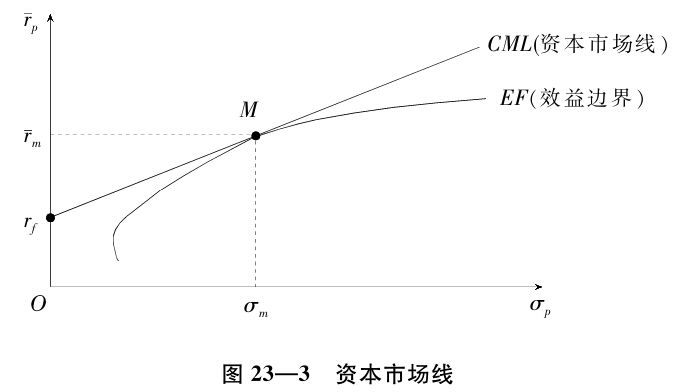

舉例,有無風險資產F與風險資產組合M,兩者的風險與收益如下:

設F與M有四種組合,每種組合的風險與收益如下:
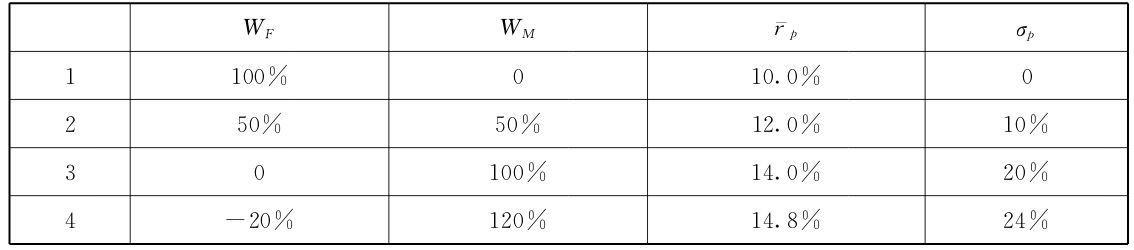
將計算出來的組合風險與收益描畫到座標圖上,我們會發現一條向上傾斜的、與效益邊界相切的直線。
為得到資本市場線,經濟學家做了三個基本的假設:第一,假設資本市場是完善的市場,這意味著市場中買方和賣方的數量足夠多,使得任何一筆交易不會影響市場的價格,所有的投資人都是市場價格的接受者而非操縱者;第二,不存在交易成本以及干擾資金供求的障礙,因而市場的摩擦成本最低;第三,存在一種無風險資產,可以允許投資者投資或借貸。
只要存在有可能按照無風險利率投資、借貸的機會,投資人就會更願意持有無風險資產F和風險資產組合M。從圖23—3可以看出,由於CML除了與效益邊界的切點M以外,其他各點均位於效益邊界的上方。從以相同的風險追求最高收益的動機出發,選擇在資本市場線上的投資組合效果最優。由此,即可進入對資本資產定價模型的討論。
資本資產定價模型
資本市場線以公式表示為:

公式右邊分為兩部分:第一部分用無風險利率表示投資的機會成本補償;第二部分表示投資的風險溢價。於是,對資產組合期望收益率的計算有了比第一節更簡化的方法。
但是,由資本市場線公式得出的期望收益率並沒有針對某一個資產,因而無法解決某個資產的定價問題。經濟學家希望能在資本市場線公式的基礎上進一步發展,得到單個資產的期望收益率。
這需要先弄清一個問題,即單個風險資產,如股票,其收益率與市場組合收益率之間的關係。首先假定,投資人持有的是一組資產而不是單一資產。因此,對於每一項資產,投資人所關心的不是該資產本身的風險,而是持有該資產後,對整個資產組合風險的影響程度。在這個基礎上,確定該資產的風險補償以及期望收益率。
單個資產對整個市場組合風險的影響可以用β係數表示。這一系數相當於資產i與市場組合——包括資產i在內的市場組合——的協方差同市場組合方差之比:

資本資產定價模型反映的是一個特定資產的風險與其期望收益率的關係。公式右邊的第一項表示投資的機會成本補償,用無風險利率表示,第二項表示投資的風險補償,用對於市場風險溢價調整以後的數據表示。
特定資產風險與預期收益率的關係可以用證券市場線SML表示,見圖23—4:
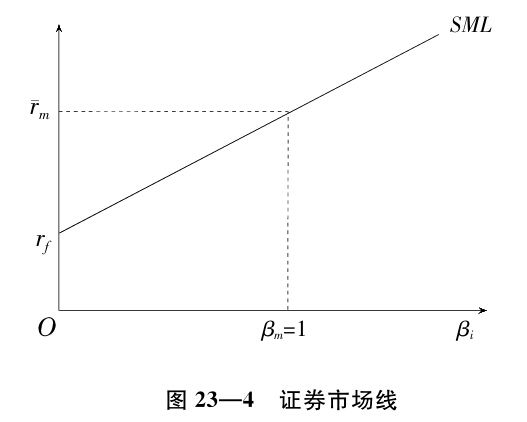
證券市場線是以無風險利率為截距、斜率為r-m-rf的直線。它直觀地表現出特定資產的風險與期望收益率的關係。
到這裡,我們就基本解決了通過資本資產定價模型尋找與資產風險匹配的貼現率的問題:只要給定特定資產的β係數,以及無風險利率和市場風險溢價,就可以得出該資產的期望收益率。
例如,已知目前的無風險利率是3%,市場組合的風險溢價是5%,如果某股票的β係數是1.5,那麼,該股票的期望收益率就是:
3%+1.5×5%=10.5%
用這個期望收益率作為評價該資產價值的貼現率,對預期現金流進行貼現,就可以完成用現金流貼現法評價資產價值的過程。
資本資產定價模型以及資本市場線表示的是在市場均衡狀態下單個資產的期望收益率與風險的關係。但市場並不總是處於均衡狀態的,這時,資產價值或被高估或被低估,表現為按照市場價格計算出來的投資收益率高於或者低於用資本資產定價模型計算出來的值,在圖23—4中,則表現為相關的點或落在SML直線的上面,或落在下面。如果某隻股票的收益率大於或小於用資本資產定價模型計算出來的收益率,則意味著該股票的價值已經被低估或者高估,投資者可以決定是買進還是賣出該股票。
資本資產定價模型是現代金融學研究中具有里程碑意義的成果。正因為此,後人對其進行了大量的實證研究,以求其在理論研究和實踐中具有正確的指導意義。但實證研究的結論引起了大量的、進一步的討論,而一些研究結果顯示,β係數與資產的平均收益率之間的關係並不密切。於是,人們在資本資產定價模型基礎上進一步研究,並形成了一些新的資產定價模型。
多要素模型與套利定價理論簡介
資本資產定價模型認為,人們可以很好地通過證券市場,特別是股票市場,進行分散化投資並從而規避非系統性風險。因此,定價公式中只需要考慮對市場風險的補償。但是,一些經濟學家認為,這樣的分析過於籠統。影響經濟生活中總體市場風險變化的因素很多:除了資本資產定價模型所考慮的市場風險——證券市場風險——以外,如國民收入增長率和未來的收入水平、利率水平、能源價格、消費品價格等等——相對於資本資產定價模型所指的市場風險,被統稱為非市場風險,都是投資者事實上不能不考慮的因素。如果能在資本資產定價模型的基礎上再增加一些風險因素,就會使模型的表達更為準確。
1973年,羅伯特·默頓提出了多要素模型(multifactor CAPM)。
假定除了市場——證券市場——風險以外,還存在n個影響資產收益率的非市場風險因素,則資本資產定價模型可以改寫為多要素模型:

多要素模型的價值在於承認了非市場因素在資產價值確定中的作用,缺點是很難操作,不容易確認並估計所有的非市場風險。
套利定價理論(arbitrage pricing theory,APT)是1976年由斯蒂芬·羅斯建立的。該理論假定資產的期望收益率受多個因素的影響,在這一點上與多要素模型一致。但是,與CAPM以及多要素CAPM不同的是,套利定價理論強調套利行為在建立市場均衡過程中的作用。例如,一旦出現價格失衡,按照風險收益均衡的規律,投資者會自動調整資產組合直到市場恢復均衡。