e5 黄達 金融學 v3
第三節 利率的期限結構
什麼是利率的期限結構
在由多種多樣利率所構成的系統中,存在著種種結構。其中,利率的期限結構(term structure of interest rates)特別受到關注。
任何一種利率大多對應著不同期限。如存款利率,對應著長短不同的期限而高低不同,這是存款利率的期限結構;國債利率,對應著長短不同的期限有高有低,這是國債利率的期限結構等等。由於市場經濟中的利率是不斷變動的,所以利率的期限結構總是某年、某月、某日的期限結構。例如,表12—1所表示的就是2008年4月17日和2012年4月26日美國政府債券的利率期限結構。概括說來,同一品類的不同期限的利率構成該品類的利率期限結構;而期限結構則是利率與期限相關關係的反映。需要注意,利率期限結構只能就與某種信用品質相同的債務相關的利率,或同一發行人所發行的債務相關的利率來討論;加入信用品質等其他因素,期限則無可比性。
在第十二章第一節講過基準利率,其他任何利率品種都是在它的基礎上加上一定百分點的風險溢價得出的。因此,一般選擇基準利率的期限結構來表示一個經濟體的利率期限結構。第十二章第一節也提到,一個社會中最理想的基準利率是在良好的國債市場上表現出來的收益率。所以,這個市場上不同期限國債的收益率的組合,就成為該經濟體利率期限結構的代表。
利率期限結構對於金融活動具有十分重要的意義。各種債券價格的制定都是以它為基礎的。比如,某個被評為BB級的企業欲發行3年期債券,債券的發行價格以及票面利率的確定就需要參照這個時候市場上同期國債的收益率,並考慮在它的基礎上按照風險程度所應增加的百分點,形成該企業債券的收益率;然後,在企業債券收益率的基礎上確定債券的發行價格或者債券的票面利率。此外,利率期限結構也可以幫助確定其他金融產品(如股票)的價格等。
在我國,利率期限結構的研究也已開展,並已開始進入實用之中。
即期利率與遠期利率
對於研究利率的期限結構,有些習用的術語需要解釋。即期利率(spot rate of interest)與遠期利率(forward rate of interest)是其中的一對重要概念。
即期利率是指對不同期限的債權債務所標示的利率。遠期利率則是指隱含在給定的即期利率中從未來的某一時點到另一時點的利率。
以2年期儲蓄2.40%的利率為例進行分解。
——以1000000元儲蓄,兩年到期的本利和是:
1000000×(1+0.024)2=1048576(元)
——兩年儲蓄中的第一年,其行為與儲蓄一年定期沒有差別,所以,從道理分析,應按一年定期儲蓄利率計息。在一年期末,其本利和應是:
1000000×(1+0.0225)=1022500(元)
——如果是存一年定期,這時就可自由處理其本利和。假如無其他適當選擇,再存一年定期,到第二年末得本利和:
1022500×(1+0.0225)=1045506.25(元)
較1048576元少3069.75元。
——存兩年定期儲蓄,之所以可多得3069.75元,那就是因為放棄了在第二年期間對第一年本利和1022500元的自由處置權。這就是說,較大的效益是產生於第二年。如果說,第一年應取2.25%的利率,那麼第二年的利率則是:

由於是推算出來的,所以也常常稱之為隱含的遠期利率。
這裡用儲蓄利率舉例,只是由於居民儲蓄利率較為大家所熟悉。債券等利率的即期利率與遠期利率的關係也均如此。本節一開始就指出,利率期限結構的研究主要是以債券為對象展開的。以下討論均就債券舉例。
到期收益率
在第一節講到收益率時提到,由於債券的投資收益不僅取決於票面利率,同時還取決於其市場價格,所以要計算收益率。
到期收益率(yield to maturity)是指在如下兩者的金額相等時所決定的現實起作用的利率:(1)到債券還本時為止分期支付的利息和最後歸還的本金摺合成現值的累計,在翻譯的有關書籍中通常表述為“債券現金流(cash flow)的當前價值”;(2)債券當前的市場價格。設每年付息,期終還本,還有n年到期的國債,其面值為P,按票面利率每期支付的利息為C,當前的市場價格為Pm,到期收益率為y,則y可依據公式(22·12)和公式(22·13)算出近似值:
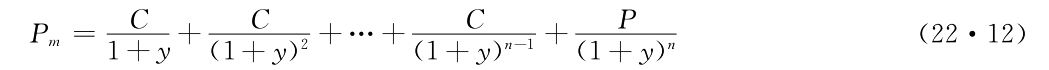
根據公式(22·12)可簡化為:

到期收益率相當於投資人按照當前市場價格購買債券並且一直持有到期滿時可以獲得的年平均收益率。它的存在使不同期限從而有不同現金流狀態的債券收益具有可比性。
到期收益率取決於債券面額、債券的市場價格、票面利率和債券期限。不過,在債券償還期內,面額、票面利率和期限是不會變化的(除非是浮動利率債券的票面利率可變)。因此,影響到期收益率變化的基本因素就是債券的市場價格。有太多的事情會影響債券價格波動:中央銀行的再貼現率調整、債券發行人的資質狀況、通貨膨脹預期、債券剩餘期限、股票市場價格波動,乃至政局、戰爭等等。由於債券價格變化直接引起債券到期收益率變化,因此,債券到期收益率幾乎就是債券價格的另一副面孔。有不少債券市場直接用到期收益率對債券標價,交易人員則按照到期收益率而不是債券價格進行交易。
我國的有關單位已計算和公佈了國家債券和金融債券的到期收益率,計算的公式就是公式(22·12)的具體化。
收益率曲線
收益率曲線(yield curve)是對利率期限結構的圖形描述。
第十二章表12—1提到2012年4月26日美國政府債券收益率,據此可以繪出收益率曲線,如圖22—3所示。
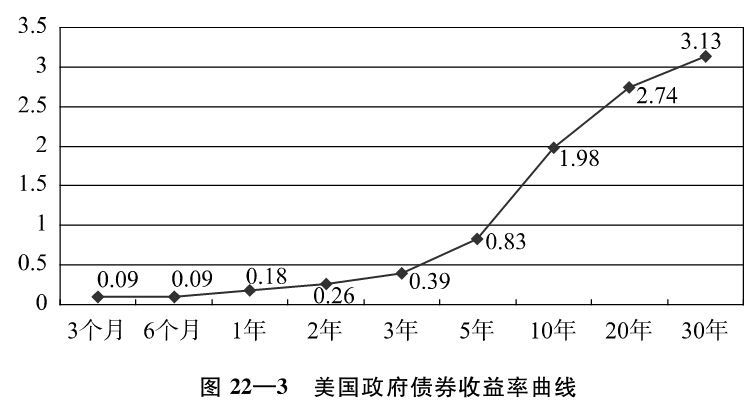
資料來源:美聯儲網站,2012-04-26。
依據同樣原理描繪出的我國債券收益率曲線,如圖22-4。
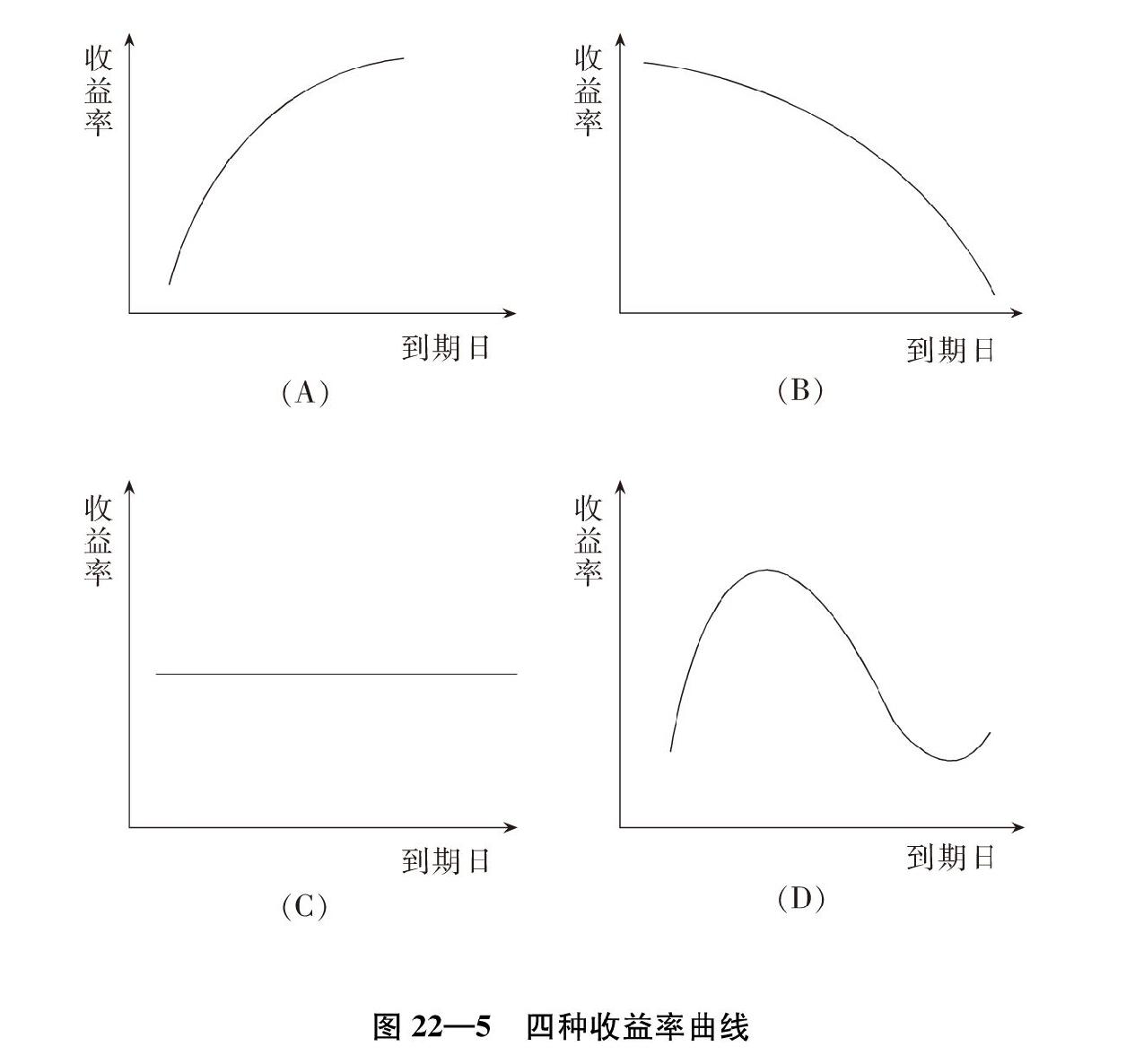
根據過去不同時日的到期收益率繪製出來的收益率曲線形狀各異。如何加以歸納,有不同的處理。其中之一是歸納為四種基本圖形(見圖22—5):(1)向上傾斜狀,我國現在開始繪製的收益率曲線也是向上傾斜的;(2)向下傾斜狀;(3)水平狀;(4)駝峰狀。
為什麼收益率曲線不是簡單向上傾斜,體現期限越長、利率越高的結果?形成曲線種種不同走勢的原因是什麼?不同的曲線走勢會給未來的利率預期提供什麼信息?這些都是利率期限結構理論的重要內容。
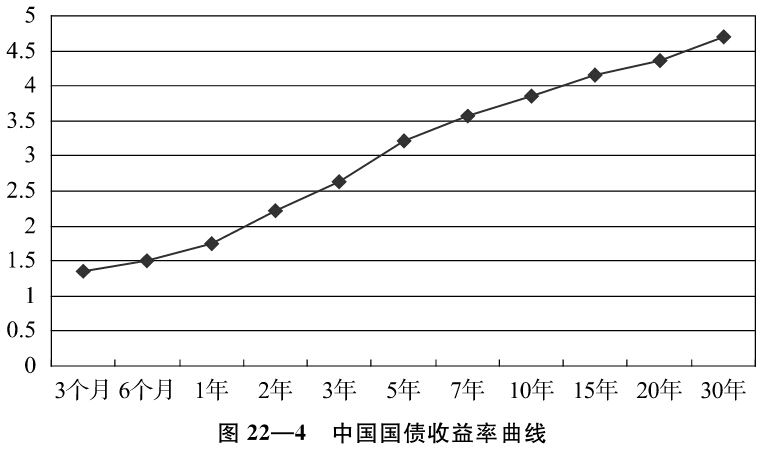
資料來源:中國債券信息網,2012-04-26。
影響利率期限結構的因素
對於影響利率期限結構的因素解釋主要有:人們對利率的預期,人們對流動性的偏好,資金在不同期限市場之間的流動程度等。比較經典的解釋理論有預期理論(expectation theory)和市場隔斷理論(market segmentation theory)。其中,預期理論又可以分為純預期理論(pure expectation theory)、流動性理論(liquidity theory)和偏好理論(preferred habitat theory)。
預期理論的共同特點是,對遠期利率的行為有共同假設:都同意預期未來短期利率,或遠期利率的變化方向決定收益率曲線的形態;同時,假定當前長期債券中的遠期利率與市場對未來短期利率的預期有緊密聯繫。預期理論中的流動理論和偏好理論認為,除此以外還有其他因素會影響預期的未來利率,而純粹預期理論則排除其他影響因素。
預期理論認為,預期的未來短期利率影響了收益率的曲線;而純粹預期理論認為,只有遠期利率代表預期的未來短期利率,並且只有遠期利率,或者預期的未來短期利率,決定收益率曲線的形狀。既然遠期利率在收益率曲線的解釋中有如此重要的作用,我們有必要對它作進一步瞭解。
設想一位投資人有一筆可作4年投資於債券的資金。作為投資對象的債券多種多樣,在其中,選中兩個投資選擇進行比較:
(1)購買4年期債券,簡稱長期投資方案。
(2)購買2年期債券,到期後再購買2年期債券,簡稱短期投資方案。
用長期投資方案,投資人可以立即知道該投資的到期收益率。因為債券的市場價格、票面利率是已知的。比如當前4年期面額100元按年付息的債券,其市場價格是98.74元,票面利率是10%。用到期收益率公式,可以計算出該債券的到期收益率是10.4%。用短期投資方案,投資人則不能準確地知道整個投資期的收益率。他只能依據所投資的2年期債券的市場價格和票面利率,計算出第一個2年期投資的到期收益率。假定目前2年期按年付息的債券,其市場價格是99.65元、息票利率是9%,於是,計算得知到期收益率是9.2%。但是,投資人不知道這一筆2年期債券到期並從而需要再次購買2年期債券時,債券的市場價格會有怎樣的變化。當然,投資人也就無從計算該資金第二次投資於2年期債券的到期收益率,從而也就不可能判斷整個4年的投資收益率。
在假設投資人不考慮風險因素的情況下,選擇哪一種方案投資,就取決於哪一種方式可以提供更高的收入。如果兩種方式的投資收入都一樣,投資人選擇哪種方式投資是沒有區別的。這裡提出的問題是:投資人預期未來——在這個例子中是2年期滿之際——的短期利率處於怎樣的水平才能達到這種“無區別”的狀況。
設預期未來利率f能夠使兩種投資方案的未來收入一樣,根據上面關於即期利率與遠期利率的分析可以列示如下:
100×(1+10.4%)4=100×(1+9.2%)2×(1+f)2
不難解出,f=11.6%。
如果預期未來短期利率f大於11.6%,短期投資方案的總體收入會大於長期投資方案,投資人傾向於選擇短期投資;反之,投資人傾向於選擇長期投資。
在一個充分競爭和資金自由流動的市場上,活躍的套利活動會使兩種投資方案的收益率差異消失,也就是說,使兩者具有相同的收益率。例如,假如f小於11.6%,投資人會傾向於長期投資方案,因而導致長期資金供應增加,長期債券價格上升,收益率下降,直到長期投資收益率等同於短期投資的收益率。這時,投資人會停止追逐長期投資的行為。假如f大於11.6%,投資人會傾向於短期投資方案,因而導致短期資金供應增加,短期債券價格上升,收益率下降,直到投資人停止追逐短期投資的行為。因此可以認定,在市場充分競爭的假設前提下,長、短期投資會趨向於具有同等的投資收益率。
根據純粹預期理論,遠期利率或預期未來短期利率的變化決定了利率的期限結構和收益率曲線形狀。而一定時間的利率期限結構反映了當前市場對未來一系列短期利率的預期:當預期未來短期利率上升時,會有上升的收益率曲線;反之,收益率曲線是下降的。換言之,上升的收益率曲線代表了人們對未來利率上升的預期,下降的收益率曲線代表了人們對未來利率下降的預期。
從人們根據利率預期調整自己的金融活動行為的結果看,對未來短期利率的預期的確可以改變收益率曲線。這可從投資人、投機人和籌資人三方面進行分析。假設預期未來短期利率上升,對長期投資感興趣的人會因為長期債券價格下降幅度大於短期債券價格下降幅度,就會放棄持有長期債券,轉而持有短期債券。於是,造成短期債券的需求增加、價格上升、收益率下降,而長期債券則價格下降、收益率上升。這就促成收益率曲線向上傾斜。對於投機者來說,會利用利率上升從而債券價格下降的預期,拋出長期債券,或賣空長期債券,取得投機收入。當然,這種投機行為的結果也會促成收益率曲線向上傾斜。對於籌資者來說,既然未來短期利率有可能上升,那麼,聰明的做法是獲得長期資金而不是短期資金。這種做法增加了市場上長期債券的供應,幫助長期債券價格下降和到期收益率上揚。
純粹預期理論關於投資人不在意風險的假設,與現實是有出入的。實際上,由於長期債券往往具有較大的價格波動風險,這使投資人對於不同期限的投資有不同的補償要求,從而不同期限的投資策略會有不同的收益率。例如,對於一個有5年投資期的投資人來說,購買5年期債券和購買30年期債券的風險是不同的,兩種投資策略的收益率也會有所不同。
流動性理論,在純粹預期理論的基礎上,提出債券期限從而流動性也會影響收益率曲線的觀點。該理論認為,既然期限長的債券價格波動風險比短期債券大,人們自然會對這部分風險要求補償,即要求流動性風險補償。因此,只有在長期投資的收益率高於短期的平均預期收益率條件下,人們才會選擇長期投資工具。於是,期限越長的債券,到期收益率應該越高。按照流動性理論的觀點,收益率曲線一般應該是向上傾斜的;只有在預期未來短期利率下降到一定程度,以致使流動性補償無法抵消預期利率下降的程度時,才會出現下降的收益率曲線。顯然,流動性理論已經調整了純粹預期理論中關於投資人不介意風險的假設。
偏好理論接受了人們對未來短期利率的預期會影響收益率曲線的觀點,但不贊同流動性理論中的觀點。該理論並不否定收益率中包含對各種風險的補償,不過偏好理論認為,期限越長的債券中包含越多流動性風險補償的觀點,只有在市場上所有的投資人均傾向於以儘快速度出售持有的債券,而所有的籌資人均要籌借長期資金的情況下才會發生。但這種情況事實並不存在。偏好理論認為,影響收益率曲線的另一個因素應該是不同期限資金市場的供求。當一個特定期限的資金市場上供求嚴重不均衡時,交易雙方才會轉向供求狀態並非嚴重不足的其他期限的資金市場。這種資金的流動則會影響收益率曲線,使其表現出或者向上、或者向下、或者水平、或者駝峰狀的形態。
市場隔斷理論與預期理論完全不同,該理論認為資金在不同期限市場之間基本是不流動的。這倒不是行政力量限制,而是金融機構的特定業務運作所導致的對資金期限的特定要求使然。不同金融機構有不同的負債性質,因而對資金的期限有特定需求。比如,商業銀行對資金的需求主要是短期的,不會輕易到長期資金市場上融資。這種不同期限市場上資金流動的封閉性,決定了收益率曲線可以有不同的形態。例如,當長期市場上資金供過於求,導致利率下降的同時,短期市場資金供不應求,導致利率上升,就會形成向下傾斜的收益率曲線。
【複習思考題】
1.瞭解我國金融機構計息的方式。在什麼場合用單利,什麼場合用複利?
2.倘若你在銀行有一筆儲蓄存款,當儲蓄存款利率下調時,你會根據怎樣的判斷做出反應?
3.利率與收益率之間是什麼關係?如何度量收益率?
4.票面利率、收益率、到期收益率的異同何在?
5.什麼是利率的風險結構?為什麼企業債券的利率通常要高於相同期限國債的利率?
6.什麼是利率的期限結構?運用期限結構理論解釋為什麼收益率曲線會有不同的形狀?
7.從中國債券信息網查一查我國國債市場上利率期限結構的計算方法。