第四篇　金融運行的微觀機制

第二十二章　利率的風險結構與期限結構

第一節　利率的度量

概念和計算公式

利息計算中有兩種基本方法：單利（simple interest）與複利（compound interest）。

單利的特點，是對已過計息日而不提取的利息不計利息。其計算公式是：

式中，C為利息額；P為本金；r為利息率；n為借貸期限；S為本金和利息之和，簡稱本利和。例如，一筆為期5年、年利率為6%的10萬元貸款，利息總額為：

100000×6%×5=30000（元）

本利和為：

100000×（1+6%×5）=130000（元）

複利是將上期利息併入本金一併計算利息的一種方法。如按年計息，第一年按本金計息；第一年末所得的利息併入本金，第二年則按第一年末的本利和計息；第二年末的利息併入本金，第三年則按第二年末的本利和計息；如此類推，直至信用契約期滿。中國對這種複利計息方法通俗地稱為“息上加息”。其計算公式是：

若將上述實例按複利計算本利和和利息，則分別是：

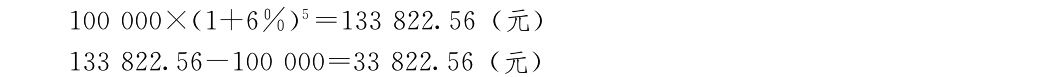
即按複利計息，可多得利息3822.56元。

為了說明單利、複利的差別，人們舉出過各式各樣的例子。假設在紀元元年元月元日貸出1盎司黃金，如果年率為3%，到2001年年底，本利和分別按單利和複利計算，其結果是：

簡言之，在確定的借貸期內，按複利計息的次數越多，投資人的利息收入就越高。當然，籌資人的利息成本也就越大。

複利反映利息的本質特徵

過去多年來，在我國有一個奇怪的現象：承認利息客觀存在的必要性，卻不承認複利。似乎單利可以同社會主義相容，而一提複利，立即就與“利滾利”、“驢打滾”聯繫起來，似乎是剝削、是罪惡。

其實，無論是單利還是複利，都是利息的計算方法，而無論是哪種方法計算出來的利息，按勞動價值說，都是勞動者所創造的價值：在資本主義社會，反映的是資產階級佔有剩餘價值；在社會主義社會則是歸社會支配的剩餘勞動產品。所以，採用不採用哪種方法都不會改變利息的社會經濟性質。就形式來看，不論哪種經濟理論，利息的存在，就是承認了資本可以只依其所有權取得一部分社會產品的分配權利。如果承認這種存在的合理性，那就必須承認複利存在的合理性。因為按期結出的利息屬於貸出者所有。假定認為這部分所有權不應取得分配社會產品的權利，那麼本金的所有權也就不應取得這種權利。簡言之，否定複利，也必須否定利息本身；否則，只不過表明是自己在製造混亂。

事實上，我國銀行的告示牌上雖然均以單利標示，但實際一直沒有能夠否定複利原則。以我國儲蓄利率為例，可以非常清楚地說明這個問題。比如，定期1年的儲蓄利率必須保證按這樣的利率所計算出來的1年的利息要大於按活期儲蓄的月利率用複利方法所計算出來的1年的利息。例如，1971年10月——那時是在“文化大革命”期間，是最“革命”的時候——調整的儲蓄利率，活期月利率為0.18%，1年定期年利率為3.24%。活期存1年的利息回報（按單利計為2.16%；按複利計為2.18%）均低於3.24%。至於不同期限的定期儲蓄，按單利，當然年限越長，利率越高。以1999年6月調整的定期儲蓄年率——依然是單利——為例，1年期的為2.25%，2年期的為2.43%，3年期的為2.70%，5年期的為2.88%。這樣的利率系列保證：1年期儲蓄到期立即提取並把本利和再存入1年定期，到第2年期滿取得的累計利息回報，小於按公佈的2年期單利所取得的回報；2年期儲蓄到期立即提取並把本利和再存入3年期的儲蓄，到第5年期滿所取得的利息累計回報，小於按公佈的5年期單利所取得的回報，依此類推。也就是說，換算為複利表示，也必須是期限短的低，期限長的高。把2.43%、2.70%、2.88%換算為複利，分別為2.40%、2.63%、2.73%，完全符合這樣的要求。其實，無論哪個年份，也無論哪種存貸款利率，都是本著這樣的原則設計的。當然，也不排除有特殊事例（比如出於不鼓勵定期存款，不鼓勵長期性存款過快增長的特殊政策要求等）。但不論如何，從原則上說，複利的規律是不能違背的。否則，人們就不會存定期儲蓄，更不會存期限長的定期儲蓄。

還有一種說法：複利計算複雜，老百姓不好掌握。這是想當然的解釋。中國的老百姓，包括農民，千百年來就懂得“利滾利”；在20世紀中葉之前的新舊銀錢業也廣泛使用複利。其實，在只公佈單利率的條件下，“老百姓”在比較不同期限（比如1年定期儲蓄與3年定期儲蓄）的利息回報時，習慣的思考方法是，先算算存1年定期，到期提取並立即連同利息再存入，如此反覆，到3年期滿可獲多少利息，再與存3年定期可獲得的利息加以比較。也就是說，人們並不因不公佈複利而不進行復利的計算。

應該說，複利較單利，是更符合生活實際的計算利息的觀念。現在，在我國的經濟生活中，複利的運用實際已經極其廣泛，只是官方掛牌的利率還維持著單利的面孔。

兩個有廣泛用途的算式

在我國銀行儲蓄存款業務中，有一種零存整取，還有一種整存零取。前者是每月（或每週、每年）按同一的金額存入，到約定的期限本利和一次取出。其算式是：

式中，P為每月（或每週、每年）存入的金額；n為依次存入的次數。假如預計10年之後需要支用2萬元，估計月利率比如說為0.8%，那麼每月存入100元即可達到這個數量（確切數字為20181.92元）。

後一種整存零取是一次存入若干金額的貨幣，在以後的預定期限內，每月（或每週、每年）提取同一金額的貨幣，當達到最後期限的一次提取時，本利全部取清。其算式是：

式中，P為每月（或每週、每年）提取的金額；n為依次提取的次數。假如希望在10年內每月提取100元作為生活費，估計月利率比如說也是0.8%，那麼現在只需要存入7700元（確切數字為7695.52元）即可。

這兩個算式有很廣泛的用途。如在消費信貸中，還款的安排，通常是在貸款實施之後至約定的到期之間，如多少年，分月按同等金額支付，期滿還清。這屬於定期定額還清貸款的方式，很顯然要採用“整存零取”的算式設計。前面在介紹中國高利貸中的“印子錢”也是屬於定期定額還清貸款的方式，只是不清楚那時是怎樣求出這樣的精確解。至於在類如養老年金的設計中，前者是典型的年金終值計算公式，而後者則是典型的年金現值計算公式。“終值”、“現值”的概念下面立即講述。此外，在設計折舊提存方案等諸多方面，或需利用其中某一算式，或需兩個算式結合運用。

現值與終值

由於利息成為收益的一般形態，所以任何一筆貨幣金額，不論將作怎樣的運用，甚至還沒有考慮將作怎樣的運用，都可根據利率計算出在未來的某一時點上，將會是一個怎樣的金額。這個金額就是前面說的本利和，也通稱為“終值”（future value）。如果年利率為6%，現有100000元，在5年後的終值可按複利計算式（22·3）計算，即

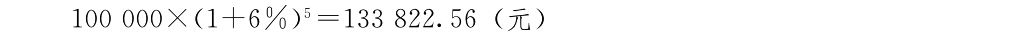
把這個過程倒轉過來，如果我們知道在未來某一時點上有一定金額的貨幣，只要把它看做是那時的本利和，就可按現行利率計算出要想取得這樣金額的本利和在現在所必須具有的本金，即

設5年後期望取得一筆100000元的貨幣，假如利率不變，現在應有的本金是：

這個逆算出來的本金稱為“現值”（present value）。這個公式叫做貼現值（present discounted value）公式。

現值的觀念有很久遠的歷史。中國過去流行一種倒扣息的放債方法，如契約上名義是借100元還100元，半年還清，在月息3分的情況下，不計複利，貸者付給借者的只是85元。現代銀行有一項極其重要的業務，即收買票據的業務，其收買的價格就是根據票據金額和利率倒算出來的現值。這項業務叫“貼現”，現值也稱貼現值（present discounted value）。

現值的運用

現值的計算方法不僅可用於銀行貼現票據等類似業務方面，而且還有很廣泛的運用領域。比如，用來比較各種投資方案時，現值的計算是不可缺少的。在現實生活中，一個項目的投資很少是一次性的，大多是連續多年陸續投資。不同方案不僅投資總額不同，而且投資在年度之間的分配比例也不同。如果不運用求現值方法，把不同時間、不同金額的投資換算為統一時點的值，則根本無法比較。下面舉例說明。

例如，現有一項工程需10年建成。有甲、乙兩個投資方案。甲方案第一年年初需投入5000萬元，以後9年每年年初再追加投資500萬元，共需投資9500萬元；乙方案是每一年年初平均投入1000萬元，共需投資1億元。從投資總額看，甲方案少於乙方案；但從資金佔壓時間看，乙方案似較甲方案好一些，不過也說不太準：第一年的投入，甲方案雖明顯大於乙方案，第二年以後每年的投入，乙方案又大於甲方案。現值的觀念則可以幫助解決這個問題。假設市場利率為10%，這樣，兩方案的現值分別如表22—1所列。

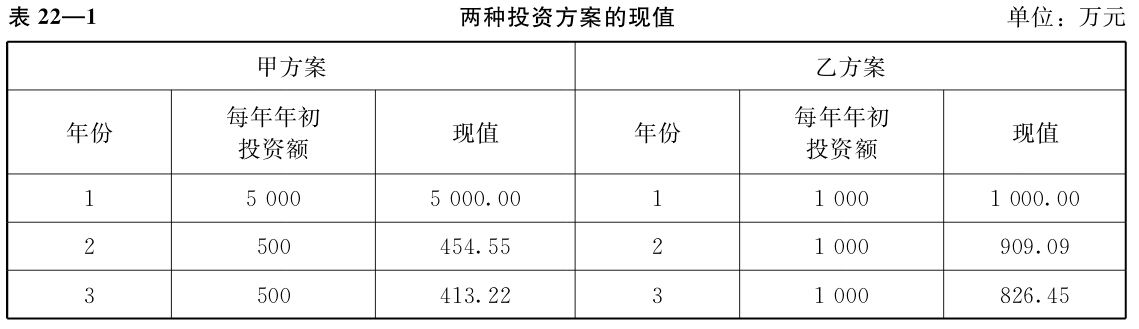
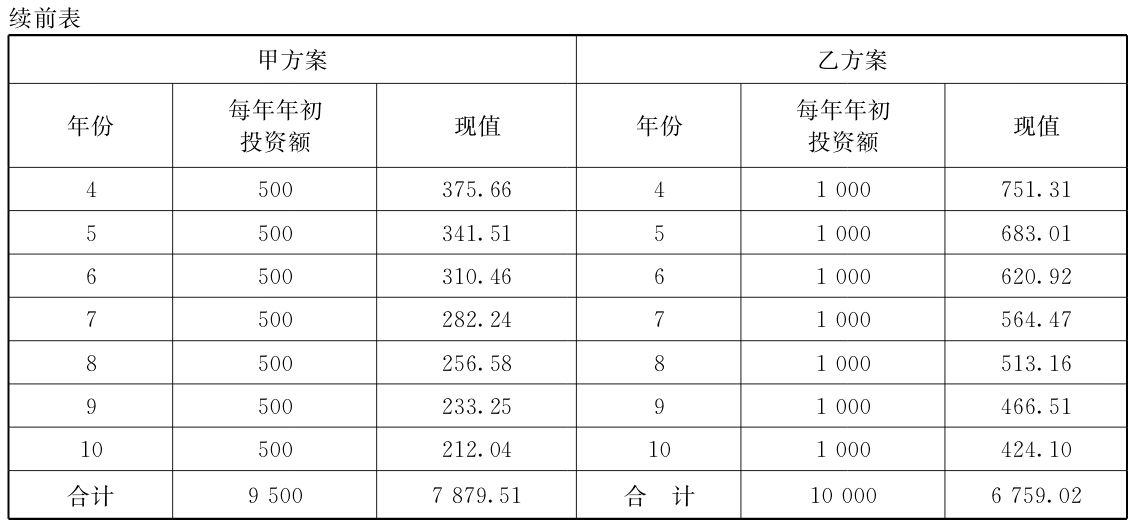
現在看起來，採用乙方案較甲方案，投資成本可以節約1000多萬元。如果其他條件類似，決策就有了明確的依據。

競價拍賣與利率

第十二章第一節在介紹基準利率時，曾提到通過競價拍賣（open-outcry auction）形成利率的問題。

在市場經濟中，不少涉及信用行為的契約並不列有利率。如有的債券只有面額而不標明利率，習稱“無息債券”。發行時採用拍賣方式。設一種面額100元半年期的債券以97元成交，那麼它的年利率，利用計算貼現值（present discounted value）的公式（22·9）計算，就是：

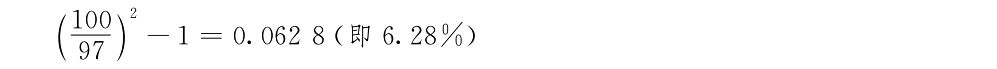
在市場經濟國家，各種債券以及許多金融工具，相當大的部分均採用競價拍賣的方式。在市場價格低於或高於面值時，不論有否票面利率，都決定了實際起作用的利率。有的競價拍賣，其標的的本身就是利率。

在我國，競價拍賣的辦法近幾年來有極其迅速的發展，如各種債券也大多采用競價拍賣的方式發行。

在美國，短期國債均採用拍賣方式。通過競價成交，實際也就意味著在這個時點上市場基準利率水平的形成。當然，這是以存在一個發達的政府債券交易市場為前提的。只要這個前提存在，市場就會每時每刻展示不同期限的基準利率。這對於金融市場上的運作，如第四篇所要研究的確定投資價格或者金融產品的價格等等，都是至關重要的。

利率與收益率

在涉及利率問題的研究和實踐中，有一個使用非常廣泛的收益率（yield）概念與利率概念並存。

收益率實質就是利率。作為理論研究，這兩者無實質性區別。而在實際生活中，由於種種原因——往往是習慣的原因——使兩者出現差別。

例如，為了對不同期限的投資項目收益率進行比較，往往需要將不到1年期的利率轉化為年率，這需要換算。在西方的一些國家，要把月率用年率來表示，習慣的做法是以12乘月率；如此算出的結果也獲得“利率”的稱謂。顯然，這樣換算極不精確。設y代表年率，r_m代表月率，精確的年率換算應該引入複利觀念，其算式應是：

為了區別於習慣的年度的利率稱謂，如此求出的y則稱為年度的收益率。

再如，類如無息債券之類，本身就沒有規定利率。要是根據拍賣成交價逆算出收益的大小，叫“收益率”極其自然。第十二章第一節講到基準利率時，表12—1列出的就是收益率。至於票面標明利率的債券，在二級債券市場上的交易中，由於價格波動，使持有者的收益大小與票面利率有別，從而也有計算收益率的問題。關於這個問題將在第三節講述。

又如，有些年金的積累和支用，有些儲蓄的零存整取和整存零取，有些消費信用的分期貸放和還款，往往只有一個總額、一個到期期限、一個期限內的分期期數和一個每期存、取、貸、還的金額；總額和分期支付額大多為整數。事實上，這類金融交易行為都是根據一定的利率設計的，但未標明。把這個隱含的利率算出來，也稱為收益率。