e1 Zvi Bodie 投資學 v10: 27.3 布萊克-利特曼模型

e1 Zvi Bodie 投資學 v10

27.3　布萊克-利特曼模型

因特雷納-布萊克模型和布萊克-斯科爾斯期權定價公式聞名的費雪·布萊克與羅伯特·利特曼提出了另一個重要的投資組合構建模型——布萊克-利特曼資模型（BL）。它允許投資組合經理對複雜的預測（他們稱之為觀點（views））進行量化並應用於投資組合的構建。^[1]在介紹該模型之前，我們將簡要介紹一下關於資產配置的問題。在下一節中，我們將比較兩個模型，瞭解模型之間的共性可以幫助我們更好地理解布萊克-利特曼（BL）模型。

27.3.1　布萊克-利特曼資產配置決策

假設某投資組合經理正在努力為下個月進行資產配置（asset allocation），投資範圍包括票據、債券和股票。為使夏普比率達到最大，投資組合應只包括債券和股票。最優化風險投資組合是與資本配置線（CAL）相切的投資組合。基金投資者根據自己的風險偏好沿資本配置線構建想要的頭寸，也就是將票據與最優風險投資組合進行組合。這些問題在第7.3節已討論過。在第7章中，我們是用一系列給定數據來優化投資組合的。但在實踐中，如果知道數據，優化問題將迎刃而解，困擾投資組合經理的難題是如何獲得數據。布萊克和利特曼提出了一種均衡考慮歷史數據和投資組合經理未來短期觀點的方法。

BL模型中的數據來自兩個方面：一個是過去的歷史數據，另一個是對未來的預測數據，叫作觀點。過去的歷史樣本用來預測資產配置中所需資產的協方差矩陣。預測所得的協方差矩陣與均衡模型（例如CAPM）一起將產生一個基準預測，這將是被動策略的基礎。接下來，觀點將被引入並進行量化。觀點代表的是相對於基準預測的偏離，這一偏離導致了對預期收益率的一系列修復。通過這些新的輸入值（類似於TB模型中的α預測），一個最優的風險投資組合將代替（不再有效的）被動投資組合。

27.3.2　第一步：根據歷史數據計算協方差矩陣

這項簡單的任務就是BL模型的第一步。假設利用短期歷史超額收益率得到的協方差矩陣如下。

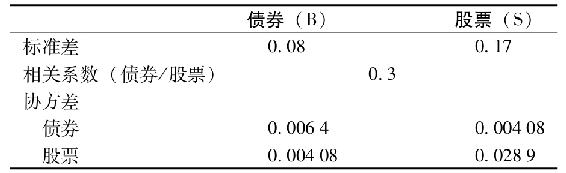
注意，這一步對於BL模型和特雷納-布萊克（TB）模型是一樣的。這一步也體現在圖27-4所示的組織結構圖中。

27.3.3　第二步：確定基線預測

由於歷史數據在預測下月期望收益率方面作用有限，BL提出了一個替代方案。他們假設當前市場是均衡的，股票和債券的價格包含了所有可獲得的信息，因此權重與市值成比例的理論市場組合是有效的，進而導出了基線預測（baseline forecast）。假設根據當前市場中發行在外的債券和股票的市值，債券的權重w_B=0.25，股票的權重w_S=0.75。將這一權重用於第一步的協方差矩陣，得到基準投資組合的方差為

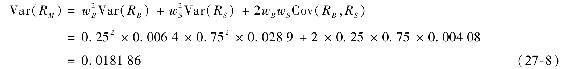
CAPM公式（第9章式（9-2））給出了市場投資組合風險（方差）與風險溢價（期望超額收益率）之間的關係

式中，A表示風險厭惡的平均係數。假設A=3，那麼基準投資組合的均衡風險溢價為：E（R_M）=3×0.018186=0.0546=5.46%。債券和股票的均衡風險溢價可根據它們在基準投資組合中的β值求出

因此，第二步得到債券風險溢價的基準預測為1.40%，股票為6.81%。

第二步的最後工作是計算基線預測的協方差矩陣，不同於債券和股票投資組合已實現超額收益率的協方差矩陣，這是關於預測精準度的報告。我們想知道的是期望收益率估計的精確性，而不是關注實際收益率的波動。約定俗成的做法是將標準差設為收益率標準差的10%（即為收益率方差的1%）。比如說，在某種特定情況下，預測下個月的經濟形勢與過去100個月相近，也就是說過去100個月的平均收益率是下個月期望收益率的無偏估計，那麼平均收益率的方差就是實際收益率方差的1%。因此，在這種情況下，用收益率的協方差矩陣乘以0.01便可以得到期望收益率的協方差矩陣，那麼第二步將得到下列預測和協方差矩陣。

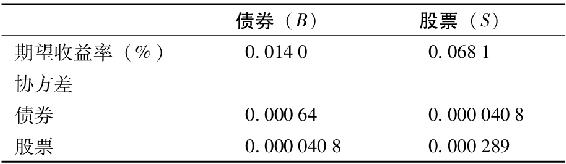
現在我們已經處理完了市場預期，接下來我們將把投資經理的個人觀點引入我們的分析中。

27.3.4　第三步：融合投資經理的個人觀點

BL模型允許投資組合經理在優化過程中引入任何關於基準預測的觀點，他們還會在這些觀點後加上自己的置信度。在BL模型中，這些觀點都被表示為各種超額收益率的不同線性組合的值，而置信度則作為這些值的誤差的協方差矩陣。

【例27-1】BL模型的觀點

假設某投資經理對基線預測持約束的觀點，具體來說，他相信債券的業績將超過股票0.5個百分點。用公式表示為

1×R_B+（-1）×R_S=0.5%

更一般地，任何觀點（即相關超額收益率的線性組合）都可以表示為一個數組（在Excel中，數組是一列數字）與超額收益率數組（另一列數字）的乘積。在本例中，權重數組為P=（1，-1），超額收益數組為（R_B，R_S）（在Excel中，這個乘法可由函數SUMPRODUCT完成）。線性組合的值，用字母Q表示，就是投資組合經理的觀點。在本例中，Q=0.5%將在優化過程中用到。^[2]

每個觀點都有其置信水平，即衡量Q精確度的標準差。換句話說，投資組合經理的觀點為Q+ε，其中ε表示均值為零時的觀點（觀點的標準差反映了投資組合經理的置信度）周圍的“噪聲”。我們可以發現，股票和債券期望收益率之差的標準差為1.65%^[3]（計算見式（27-13）），如果投資組合經理認為σ（ε）=1.73%，用R=（R_B，R_S）來表示收益率數組，那麼經理的觀點P便可以表示為^[4]

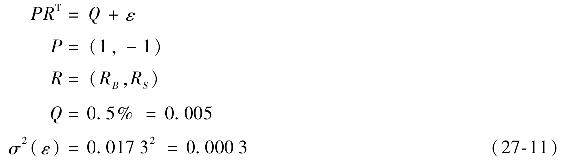
27.3.5　第四步：修正（後驗）期望

從市值及其協方差矩陣得來的基線預測構成了債券和股票收益率的先驗分佈。而投資組合經理的觀點與其置信水平一起，提供了根據“試驗”得來的概率分佈，也就是說，附加信息必須與先驗分佈最佳結合。所得上述組合的結果就是在投資組合經理觀點下的一系列新的期望收益。

為了更直觀地理解，需要思考基準期望收益率暗含了什麼觀點。從市場數據得出的預期是債券的期望收益率為1.40%，股票的為6.81%。因此，基線觀點為E（R_B）-E（R_S）=-5.41%。相比之下，投資組合經理認為這個差值應為Q=R_B-R_S=0.5%。下面我們用BL線性方程組來表示市場期望

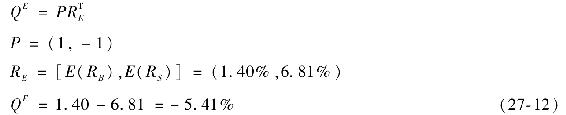
因此，基線“觀點”為-5.41%（即股票的業績會超過債券），這與投資組合經理的觀點大相徑庭，其差值D為

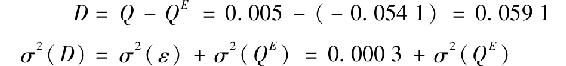
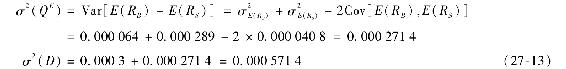
在基線預期與投資組合經理觀點相差懸殊的情況下，我們可以預計，條件期望將與基準大不相同，進而最優投資組合也會發生巨大的變化。

期望收益率的變化是以下4個因素的函數：基線期望E（R）、投資組合經理觀點與基線觀點之差D（見式（27-13））、資產對D方差的貢獻和D的方差。利用BL模型可得到

我們可以看到，投資組合經理將債券的期望收益率調高了0.24%，達到了1.64%，將股票的期望收益率下調了2.57%，變成了4.24%。股票和債券的期望收益率之差從5.41%降到了2.60%。這是一個非常大的變化，可見投資組合經理最後的觀點幾乎是其先前觀點和基線觀點折中的結果。更一般地，折中的程度與各觀點的精確度有關。

在這個例子中，我們只涉及了兩類資產和一個觀點，可以很容易推廣到多種資產和關於未來收益率的多種觀點，這比簡單的兩種收益率之差要複雜得多。這些觀點可以為資產的任何線性組合賦值，且置信水平（各觀點ε值的協方差矩陣）可以允許各觀點之間存在依存性，這種量化投資組合經理獨有信息的靈活性賦予了模型巨大的潛力。本章的附錄B展示了一般的BL模型。

27.3.6　第五步：投資組合優化

從現在開始，投資組合優化採用第7章所述的馬科維茨過程，輸入量由基線期望替換為產生於投資組合經理觀點的條件期望。

表27-7列示了BL模型的計算過程。其中表27-7a列示了基準預測的計算過程；為了得到修正（條件）期望，表27-7b引入了投資組合經理的觀點。圖27-5顯示了假設觀點正確和錯誤時，不同置信水平下以M²衡量的業績表現情況。當觀點的可信度下降時（觀點的SD上升），債券的比重下降，當觀點沒有可信度（SD非常大），債券的比重下降到0.3，這個比重由基線預測決定。在這一點，這一組合是消極的，其M²為0。

在圖中，我們還注意到，M²的形狀是不對稱的。當對觀點的可信度很高導致債券配置比重較高時，當觀點正確時，M²的增加值少於當觀點錯誤時M²的減少值。當對觀點的可信度較低導致債券配置比重較低時，這個“遊戲”在M²的得失上將變得更加對稱。由於決定觀點的標準差的大小非常抽象，這張圖告訴我們在質疑的部分犯錯相對來講是更謹慎的選擇。

表27-7　布萊克-利特曼組合對於信心水平的敏感性

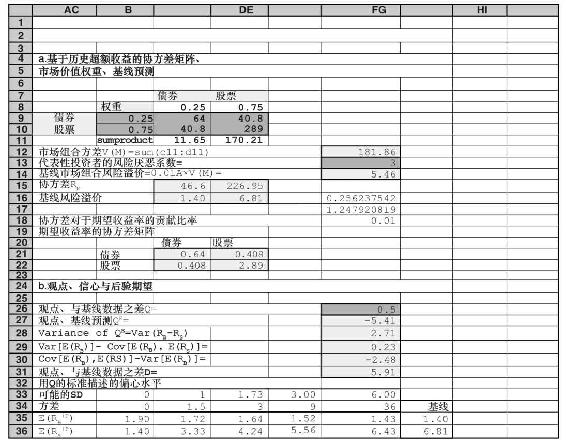
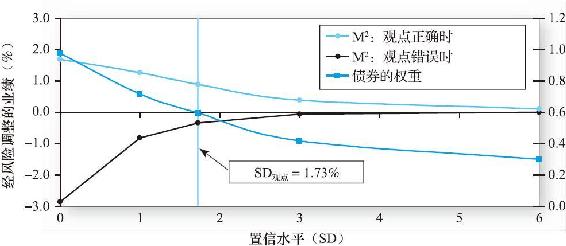
圖27-5　布萊克-利特曼投資組合業績對置信水平的敏感性分析

[1] Black and Litterman，“Global Portfolio Optimization”.

[2] 一個更簡單的觀點，認為債券的收益是3%也是合理的，這樣的話，P=（1，0），這就和特雷納-布萊克（TB）模型中α的預測很相似了。如果所有的觀點都和這個一樣這麼簡單，TB模型和BL模型就沒有什麼區別。

[3] 由於缺少能夠闡明觀點標準差的部分信息，如觀點來源的記錄，基準預測的協方差矩陣的標準差常用來代替此處收益率差的標準差。

[4] 這裡觀點被表述成一個行向量，有多少種風險資產就有相應多少收益率，這個行向量就有同樣多的元素（這裡是7個）。投資經理的觀點Q就等於P（記錄他們觀點中資產的數量）乘以他們的實際收益，其中實際收益需要加T（轉置符號，將行向量變成列向量），這樣才能求出這兩個的乘積。