e1 Zvi Bodie 投資學 v10
26.3 可攜阿爾法
市場中性純賭局的重要推論是可攜阿爾法(portable alpha)的概念。假設你想對一個你認為被低估的股票投機,但是你認為大盤會下跌。即使在該股票被相對低估方面你是正確的,但它仍然可能隨著大盤下跌。你想把純股票賭注與由股票正貝塔值引起的市場資產配置賭注區分開來,解決方案是購買股票並且通過出售足夠多的指數期貨來消除市場敞口,從而將貝塔值降到零。這種股票多頭-期貨空頭的策略使得你可以進行一場純賭局,或者說該股票的市場中性頭寸。
更一般地,你也許希望將資產配置與股票選擇分開。方法是投資於任何可以“找到阿爾法”的地方。然後你可以對衝掉系統風險,從而將阿爾法剝離出來。最終,你通過消極產品比如指數基金或者ETF來對市場的目標板塊建立敞口。換句話說,你已經創造了可以與市場任意選定板塊敞口混合的可攜阿爾法。這個過程稱為阿爾法轉移(alpha transfer),因為你把阿爾法從你發現的板塊轉移到了你最終建立敞口的板塊。尋找阿爾法需要技巧,相較之下,貝塔或者市場敞口是一種可以通過指數基金或者ETF廉價購得的“商品”。
純賭局例子
假設你管理一個140萬美元的組合。你確信組合的阿爾法是正的,α>0,但是市場也會下跌,即rM<0。因此你將針對上述錯誤定價建立一個純賭局。
下個月的收益率用式(26-1)描述,該式說明組合收益率等於“公平的”CAPM收益率(右側前兩項),加上由“殘差項”表示的公司特有風險e,加上代表錯誤定價的阿爾法
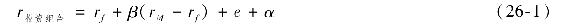
具體而言,β=1.20,α=0.02,rf=0.01,標準普爾500指數現在為S0=1344,簡化起見,組合無股利。你想要抓住每月2%的阿爾法,但你不希望被股票的正阿爾法影響,因為你預計大盤會下挫。所以,你通過售出標準普爾500期貨來對衝風險。
由於標準普爾500期貨合約乘數為250美元,組合β為1.20,通過出售5份期貨合約可對股票倉位套期保值1個月:[1]
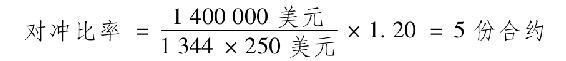
1個月後組合的美元價值為
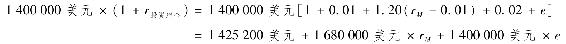
由期貨倉位帶來的收入為

概念檢查26-2
如果殘差項為-4%,市場中性倉位的美元價值和收益率將為多少?如果該月市場收益率為5%,在圖26-1每個圖上收益率位於什麼位置?
股票和期貨倉位在月末的總價值即為組合價值和期貨進項,等於
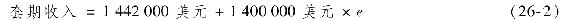
注意到期貨市場的敞口完全抵消掉了股票組合的敞口。換句話說,β值被降為零。你的投資為140萬美元,月收益率為3%加上非系統風險(式(26-2)的第二項)。這種零β倉位的合理期望收益率即為無風險利率1%,所以你可以得到2%的α,而且消除股票組合的市場敞口。
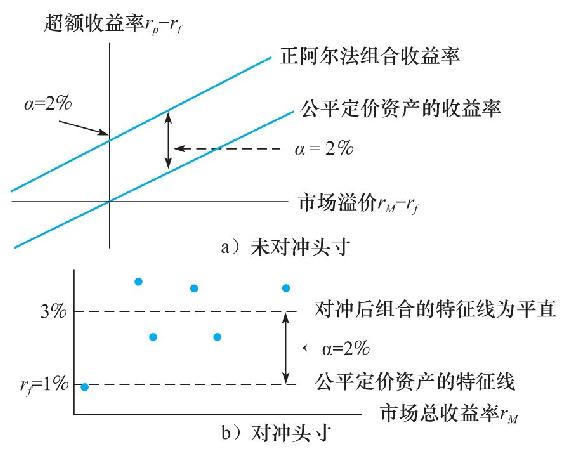
圖26-1 純賭局
這是一個純賭局的理想化示例。實際上,這個例子簡化地假定一個已知固定的組合β,但是該例說明了在對衝市場風險後對股票進行投機的目標。該目標一旦完成,藉助指數或指數期貨,你可以針對任何系統風險構建所需的敞口。因此,你實現了α的轉移。
圖26-1是該純賭局的圖示。圖26-1a示例了一個“裸露”的正α賭注,即未有套期保值。風險固定時,你的期望收益率高於均衡收益率,但由於你的市場敞口,你仍有可能在市場下挫時虧損。圖26-1b是系統風險對衝之後的特徵線,沒有市場敞口。
警告:市場中性倉位也是賭注,而且也可能失敗。這不是真正的套利,因為你的收益依賴於分析的正確性(你所察覺到的α)。此外,你也許會失敗僅僅是因為壞運氣,即你的分析準確但是特定風險(式(26-1)和式(26-2)中e為負值)仍可能導致虧損。
【例26-2】純賭局的風險
市場中性賭局在1998年時遭受了一次嚴重的質疑。儘管30 vs.29.5年國債策略(見例26-1)運行順利達數年,當俄羅斯債務違約時,事情發生逆轉,引發大量投資湧向最安全、流動性最高的30年國債。巨大的損失證明了,即使是最安全的賭注(基於趨同套利的賭注)也有風險。儘管差價最終一定會被消除,事實上數週之後也是如此,長期資本管理公司與其他對衝基金卻蒙受了巨大的損失。最後價格的趨同對於LTCM而言來得太遲了,它同時蒙受其他投資的損失,最終只得破產。[2]
由於對衝基金大量使用槓桿,即使是市場中性賭局的收益也會有巨大波動。多數錯誤定價相當微小,而多頭-空頭策略的本質使得總體波動較低。對衝基金不斷加大賭注金額,當賭注成功時加大了收益,但失敗時也放大了損失。最後,基金收益的波動自然不會小。
[1] 簡化設定期貨到期日即為套期時限,此處為1個月。如果合約到期日較長,我們需要略減對衝比率,稱為“對衝去尾”。
[2] 對於積極管理者而言,市場擇時尤為重要。我們在第12章中討論過此話題。更一般地,證券分析師察覺到錯誤定價後,他們普遍承認價格合適收斂至內在價值難以確定。