BUSINESS BOOKS

25.4　國際分散化潛力評估

首先我們來看看希望持有大量消極投資組合的投資者。他們致力於以最小的代價取得最大的分散化效果。消極投資是簡單明瞭的：它依賴於市場有效性確保廣泛的股票投資組合具有最佳的夏普比率。具體做法是估計最佳風險投資組合的均值與方差，在你願意承受的風險水平下進行資產配置以實現期望收益最高。但是現在，消極投資者必須考慮是否在自己的母國指數組合中加入國際成分。

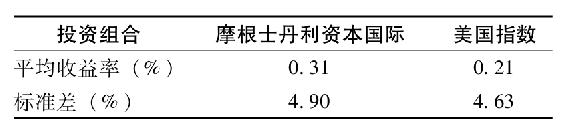
假設消極投資者依賴有效市場和全球的資本資產定價模型，那麼全球市值加權的組合就是最優的。遵守這個簡明的理論結果也是有效的。摩根士丹利資本國際（MSCI）和世界指數（ACWI）的指數基金都可以說明這一點。2002~2011年，該投資組合與美國指數投資組合的業績如下表（利用表25-9中的月收益）。

這個結果發人深省。首先，我們發現美國股票組合的風險相對較低，儘管美國投資組合可能處在世界有效邊界的內側，比世界投資組合具有更低的夏普比率，但是它比充分分散化的世界投資組合的風險更低。

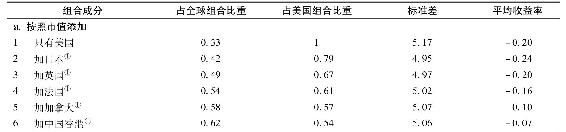
當我們意識到上述數據不支持全球CAPM時，事情就變得複雜了，因為我們無法確保全球投資組合就是最有效的。我們可以發現，高標準差的國家傾向於有高收益率，因此一個消極投資者期待找出一些簡單的規則，用以加入少量的國家（通過國際指數基金的各種組合）來淡化單一國家高標準差的劣勢並且提高整個投資組合的夏普比率。在下述三條規則中，我們從美國投資者的角度出發，利用美元計收益。我們基於市場資本化率來添加國家的原因有二：①所得的投資組合至少比較接近理論上的有效組合；②任何外國投資組合的權重都不能過大。我們根據已包含國家的數目和總組合佔全球的比例來估計日益分散的投資組合的風險。

三條篩選國家指數的簡單規則如下：

（1）股票市值規模（從高到低）。這條規則源於全球CAPM中的最優組合是以資本化加權的。

（2）關於美國的β（從低到高）。這條規則致力於降低與高風險國家有關的風險。

（3）國家指數標準差（從高到低）。這條規則源於高標準差往往帶來高收益率，而通過分散化降低單個國家的風險。

這些規則顯示了國際分散化的潛在風險與收益。其結果顯示在表25-11和圖25-16中。先看圖25-16a，鮮明展示了組合標準差隨著三條規則分散化的進程。很明顯，按從低到高的β順序添加組合（或者按照美國市場的協方差），在這12個國家或地區的標準差都大於美國的情況下，仍然迅速降低了組合風險。但是，當充分分散化後，再加入大波動的股指實際上會提高標準差。正如預料，按照標準差的順序添加國家（這次為了提高期望收益率，是從高到低的順序）則會得到最大的標準差。

表25-11　依分散化程度排列的國際組合標準差

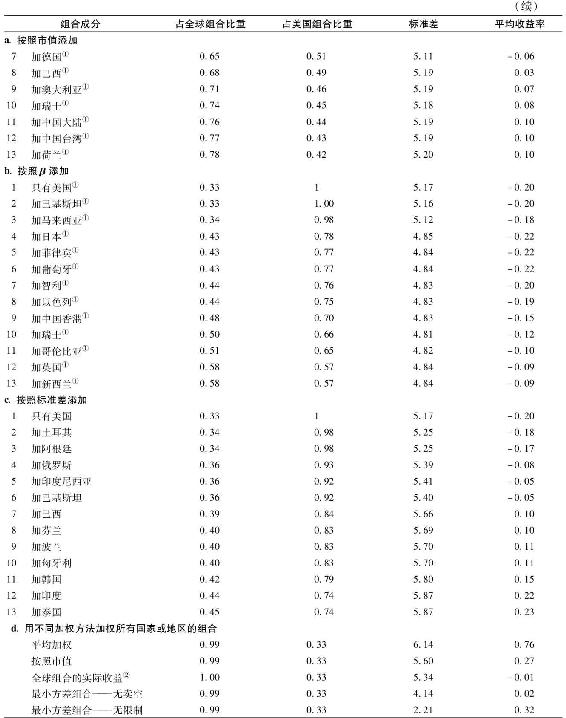
①組合按照市值加權。

②所有國家或地區（這裡忽略了五個）按照市值加權。

圖25-16b表明，按照標準差的順序加入組合也會增大平均收益率。按照β加入組合也會增大平均收益率，至少對於低β國家而言如此，這意味著至少在一定程度上，國際CAPM影響了資產定價。

總的來說，這些結果與前些章的邏輯是一致的。首先，為分散化付出了代價，回報就是風險的減小。其次，即使有強烈的母國偏見，協方差風險仍然在國際上佔有一席之地。我們也看到世界各國對風險的厭惡是類似的：高標準差的國家對應著高收益率。

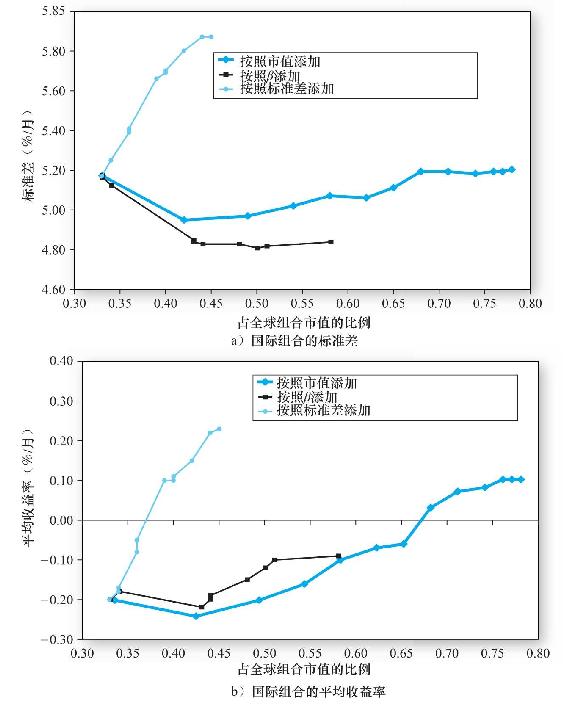
圖25-16　2000~2009年國際投資的平均收益率

表25-11d考慮加入了更加完善的國際分散化組合的收益與風險。首先看到平均加權的組合相比風險最大，與此同時，由於該組合將高風險、高收益國家的組合賦予了過高的權重，它也有更高的平均收益率。另一個極端是限制與不限制賣空時的最小方差組合。沒有賣空限制時，標準差可以達到驚人的2.21%，比最小方差國家（美國）的一半還小。但是這個組合恐怕並不可行，因為它有22個空頭，其中最大的達到-15%（瑞典）。當限制賣空時，標準差就提高到了4.14%，與市值加權的組合相比，改善有限。此外，這些組合比例也是不可行的，它包括27%在馬來西亞，而美國只佔7%。

表25-11中一個有趣的現象是世界指數（ACWI）的平均收益率低於44個國家投資組合的平均收益率。這個不同源於MSCI國家指數組合並非市值加權，而是產業加權組合，從而給予大型股票更大的權重。由於2000~2009年小型股票業績更佳，ACWI投資組合的收益率自然會降低，但是這並非必然現象，也就是說，未來並非一定如此。