e1 Zvi Bodie 投資學 v10

24.4　市場擇時

從根本上說，市場擇時解決的是何時在市場指數基金和安全資產之間轉移資金的問題。這裡所指的安全資產是指國庫券或貨幣市場基金，決策的依據是市場作為一個整體其表現是否優於安全資產的表現。那麼當市場表現不錯時，我們將如何考慮資金的部分轉移呢？

為簡單起見，假設某投資者只持有市場指數基金和國庫券兩種證券。如果兩者之間的比例是一定的，比如說市場指數基金佔0.6，那麼該投資組合的β值也是一定的，並且其證券特徵線就應是一條斜率為0.6的直線（如圖24-6a所示）。但是如果投資者能看準時機，在市場表現不錯時把資金轉入市場指數基金，那麼原來的證券特徵線就會如圖24-6b所示。該線向上彎曲的原因是，如果投資者能夠預測牛市和熊市，那麼他在市場上升時就會加大市場指數基金的權重，於是當rM升高時，證券特徵線的斜率也會隨之增大，這正如圖24-6b所示的曲線。

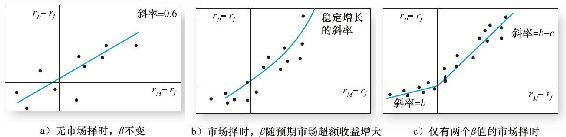
圖24-6　特徵線

特雷納和Mazuy首先提出在一般線性指數模型中加入一個平方項來估計特徵線的方程[1]：

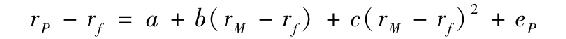
式中，rp標示投資組合收益，a、b和c是迴歸分析後所得的係數。如果c是正的，我們就能說明市場擇時確實存在，因為最後一項能夠使特徵線在rM-rf較大時相應變陡。特雷納和Mazuy利用上式對一些共同基金的數據進行了估計，但幾乎沒有找到任何投資者市場擇時的證據。

亨裡克森（Henriksson）和默頓[2]提出了另一種相似但更簡單的方法。他們假設投資組合的β只取兩個值：當市場走好時β取較大值，當市場萎靡時β取較小值。在這個假設下，投資組合的特徵線就應如圖24-6c所示。這條線的迴歸方程形式為

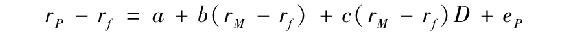
這裡D是一個虛變量，當rM>rf時，等於1，否則等於0。於是投資組合的β值在熊市時就為b，在牛市時就變成b＋c。同樣，如果迴歸得到正的c值，那就說明有市場擇時存在。

亨裡克森[3]利用上面的等式對116家共同基金進行了迴歸檢驗。他發現，儘管其顯著性水平沒有達到5%的一般要求，但c的平均值是負的（-0.07）。11家共同基金具有顯著的c正值，但同時8傢俱有顯著的c負值。從總體來看，62%的基金的市場擇時能力是負的。因此，這些結果對投資者市場擇時的能力沒有提出多少有力的證據。也許這是正常的：如果投資者的市場擇時能獲得大量的收益，那麼很難想象這個近似有效的市場會允許這些投資技術存在。

為具體說明如何檢測市場擇時的存在性，讓我們回顧表24-2。分別把投資組合P與Q的超額收益與超額收益及其平方進行線性迴歸

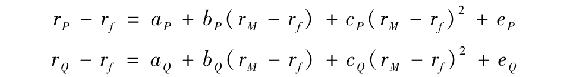
可以得到下列統計數據

括號中的數字是對錶24-3進行單變量回歸所得的估計結果，這些結果表明投資組合P不存在市場擇時。至於這到底是因為珍妮沒有在好時機時付出努力，還是因為這種努力都徒勞無功而只增加了不必要的投資組合方差，我們就不得而知了。

但投資組合Q的迴歸結果表明，市場擇時是相當成功的。市場擇時係數c的估計值為0.1，表明投資者成功地把握了時機，但所帶來的利益被不明智的股票選擇（a為負值）給抵消了。值得注意的是，投資組合Q的α值已由不存在市場擇時（不變更投資組合成分）時的5.28%降到了現在的-2.29%。

由於傳統業績評估要求固定均值和固定方差的假設，因此上文的例子同樣說明了這一假設不合理。市場擇時者可以通過適時地進入或退出市場，從而使β值和收益均值不斷髮生變化。儘管擴展的迴歸方程體現了這一現象，但傳統的證券特徵線（SCL）忽略了它。如果注意到投資組合Q相對於P來說既有時機選擇的成功，也有股票選擇的失敗，那麼在這兩種價值沒有正確評估出來之前，比較投資組合P和Q的優劣還是很難的。不過對於業績評估來說，最重要的一點是擴展的迴歸方程體現了投資組合中成分變化的效應，因此，在一定程度上它使傳統的均值-方差指標複雜化了。

24.4.1　市場擇時的潛在價值

假設理想的市場擇時是指在年初準確判斷標準普爾500指數的業績能否優於滾動購買1個月期國庫券收益的能力，相應地，投資者便可以在每年年初將所有資金都轉入會有更高收益的那一方。若從1927年1月1日開始，初始資本是1美元，市場擇時的完美把握者在86年後，也就是2012年12月31日，資產會變成多少呢？他在整個時期內的總收益與只持有國庫券或者股權的投資者相比又怎樣呢？

根據國庫券和標準普爾500指數的歷史收益，表24-4的第1~3列計算了上述三種策略的各種統計指標（在第5章中有一個類似的表格，這個表格可以在www.mhhe.com/bkm找到）。根據股票和國庫券的收益率，我們得到了2012年所有國庫券投資者和所有股權投資者的資產終值，而市場擇時的完美把握者每年的收益是股票收益和國庫券收益的最大值。

表24-4　國庫券、股權和完美與非完美時機把握者的業績

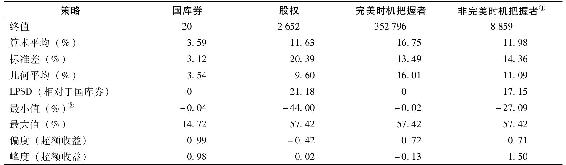
①非完美時機把握者有P1=P2=0.7和P1+P2-1=0.4。

②國庫券一列中的負值-0.06%是在1940年得到的，這個數據並非根據國庫券得出，而是根據臨近到期日的中期國債得出。

表24-4的第一行說明了很多問題，投資1美元於國庫券，86年後的終值是20美元，同樣1美元投資於股權的終值卻是2652美元。這與第5章中所提到的25年期的投資是類似的，投資期從25年延長至86年所導致的終值上的巨大差異也體現了複利計息的驚人效果。在第5章中，我們談到過，這種終值上的差異源於對股權投資者所承擔風險的合理補償。從表24-4中可以看到，全股權投資者的標準差高達20.39%，這也就解釋了為什麼股票的算術平均收益率有11.63%，但幾何平均收益率只有9.60%（請注意，幾何平均永遠小於算術平均，兩者之差隨收益率波動而增大）。

完美市場擇時者的終值是353000美元，是已經相當大的全股權投資者的133倍！實際上，這個結果比看上去還要好，因為他的收益是真正的無風險的，其投資組合的標準差（13.49%）與風險無關。由於完美時機者的收益永遠不會低於無風險收益，所以標準差只是對好驚喜的測度而已。而其分佈的正偏度（對比與股權投資者稍負的偏度）說明極值全都是正的。最大和最小收益也是它不凡表現的證明——最小收益等於國庫券的最小收益（1940年），而最大收益等於股權的最大收益（1933年），所以所有為負的股權收益率（比如1931年的-44%）都被時機者避免掉了。最後，下偏標準差（LPSD）可以通過計算低於無風險收益率的收益率標準差得到。[4]全股權組合的LPSD僅僅比傳統標準差低一點，而對於時機完美者，這個值必然是零。

如果將全股權組合終值超過國庫券終值的部分解釋為對投資風險的補償，那麼風險調整後全股權組合的終值一定等於國庫券的終值20美元。[5]相比之下，完美擇時者的組合沒有風險，因此收益不會被風險打折。因此可以這麼說，完美擇時者的預測能力將20美元的終值變成了352796美元。

24.4.2　把市場擇時作為看漲期權進行估價

評估市場擇時能力的關鍵在於意識到完美的預測等同於持有股權組合的看漲期權。市場擇時的完美擇時者總是把100%的資金投資於安全資產或者股權組合當中收益較高的那個，收益率至少是無風險利率。這在圖24-7中可以體現出來。

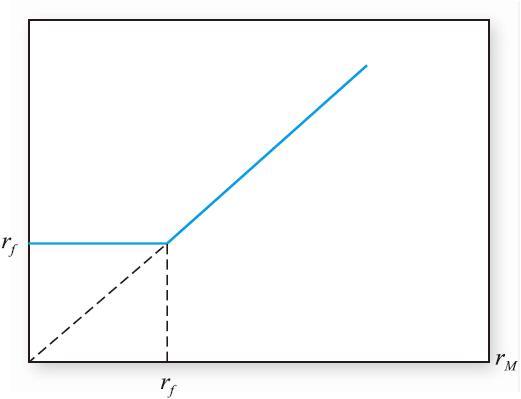
圖24-7　把完美市場擇時者的收益率表示為市場指數收益率的函數

把信息的價值看作期權，假設市場指數現在是S0，以該指數為標的的看漲期權的執行價格為X=S0（1+rf）。如果下一期市場的表現超過國庫券，ST將超過X，反之它將小於X。現在考察由此期權和S0美元國庫券投資組成的組合的回報：

當市場處於熊市時（即市場收益率小於無風險利率），該組合的收益率等於無風險利率，當市場處於牛市時，售出國庫券，組合收益即為市場收益。這便是完美市場擇時者所構建的投資組合。[6]

由於精準預測的能力相當於持有看漲期權，當無風險利率已知時，我們就可以利用期權定價模型來賦予預測能力以貨幣價值。這樣預測提供者也可以公平地對其預測服務向投資者收取費用。我們不僅可以對完美預測賦予貨幣價值，也可以對非完美預測賦予貨幣價值。

以1美元股權為標的資產的完美市場擇時者看漲期權的執行價格為國庫券投資的終值。利用連續複利計息，即為1美元×erT。將這個執行價格帶入布萊克-斯科爾斯看漲期權定價公式中，那麼公式便簡化為

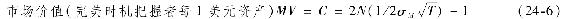
（注：把式（21-1）中，現值換為S0=＄1，令X=＄1×erT，就得到式（24-6）。）

到目前為止，我們都假設為年度預測，即T=1年。根據T=1，以及表24-4中標準普爾500指數超額收益的標準差20.39%，計算得到該期權的價值為8.12美分，即為股權組合價值的8.12%。這比表24-5中完美時機者的歷史平均收益要小，這說明市場擇時價值對於收益率分佈中的肥尾很敏感，而布萊克-斯科爾斯恰好預設了對數正態分佈。

式（24-6）告訴我們完美的市場擇時也將同樣提高每年股票收益率0.0812（每年8.12%）。因為在過去的86年裡，股權收益率達到11.63%，這將同享有年度1.1162×1.0812-1=0.2069，即20.69%收益率的年終價值一樣。

如果擇時者並非每年，而是每月做出一次正確預測，預測價值將急劇上升。當然，更加高頻率地做出預測需要更好的預測能力。由於這類預測頻率的提升並無上限，自然這類服務的價值也沒有上限。

假設完美市場擇時者每月都能做出正確預測。在這種情況下，由於預測期更短，每次預測的價值也就更小，但是每年可以有12次這樣的預測，每次都等價於一個期權，從而導致總價值上的巨大提升。在月度預測下，看漲期權的價值為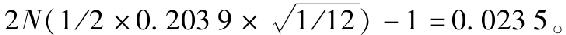根據國庫券月度收益率3.6%/12，每月的看漲期權價值為0.0235美元，可以得出1年內這些期權的現值為0.28美元。因此，相比於年度時機把握者的8.12美分，每美元月度時機把握者的年度價值為28美分。在86年的投資期內，對於1美元初始投資，預測能力的終值將遠遠增大，可達［（1+0.28）×（1+0.1163）］86=2.1×1013萬美元。

24.4.3　非完美預測的價值

不幸的是，經理不可能是完美預測者，經理能在多數時間裡正確就已經很不錯了。但是，當說到“多數時間”，並不是指一個經理正確判斷所佔的百分比。比如說，亞利桑那州杜桑市的天氣預報總是說“不會下雨”，那麼90%的天數裡它都是正確的。但是“維持”策略的高成功率根本不是預測能力的體現。類似地，對市場預測能力的恰當測度並非正確預測所佔的百分比。如果市場每3天裡有兩天是上漲的，一個每天都預測“上漲”的預測者有2/3的成功率，這顯然不能證明他的預測能力。我們需要分別計算牛市（rM<rf）的正確預測率和熊市的（rM>rf）正確預測率。

概念檢查24-4

如果一個人靠扔硬幣來預測市場，他的市場預測能力得分將有多少？

假設P1為對牛市的正確預測比率，P2為對熊市的正確預測比率，那麼P1+P2-1，就是對預測能力的正確測度。例如，一個永遠正確的預測者P1=P2=1，最終預測能力為1。而一個一直預測熊市的預測者會錯誤預測所有牛市（P1=0），正確預測所有熊市（P2=1），因此其最終預測能力為P=P1+P2-1=0。

如果擇時機者並非完美，默頓證明了如果用P=P1+P2-1測度總正確率，非完美市場擇時者的服務價值就是

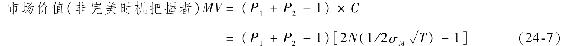
表24-4的最後一列從兩方面提供了對非完美擇時者的評估。為了模擬非完美擇時者的行為，我們取隨機數來確定每年的預測（假設P1=P2=0.7），並把86年的結果進行統計。[7]通過這種方法得到的終值“只有”8859美元，相比於完美擇時者352796美元價值，仍然遠遠高於全股權組合的2562美元。[8]

進一步考慮，由於市場中的擇時者知道自己的預測並非完美，她不會把全部資產在不同組合之間進行轉移。假定她調整寸頭，把資產的ω在國庫券和股權之間轉移。在這種情況下，可以對式（24-7）做如下改進

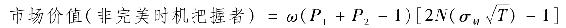
比如說，當ω=0.50（總組合的50%）時，擇時者預測的市場價值僅有完全轉移時（ω=1.0）的一半。

[1] Jack L.Treynor and Kay Mazuy，“Can Mutual Funds Outguess the Market？”Harvard Business Review 43（July-August 1966）.

[2] Roy D.Henriksson and R.C.Merton，“On Market Timing and Investment Performance.II.Statistical Procedures and Evaluating Forecast Skills，”Journal of Business 54（October 1981）.

[3] Roy D.Henriksson，“Marketing Timing and Mutual Fund Performance：An Empirical Investigation，”Journal of Business 57（January 1984）.

[4] 傳統的LPSD基於低於均值的平均平方偏差。由於這裡業績的最低起點是無風險利率，我們取的LPSD是無風險利率偏差的平方的平均值。觀測值應小於臨界值，而傳統的方法則忽略了事件發生頻率。

[5] 看上去很難把這麼大的差別完全歸咎於風險厭惡。但是這樣考慮：股本投資的終值是國庫券投資的133倍，也就是說在86年間，每年的風險溢價是5.85%：1331/86=1.0585。

[6] 這種將市場時機與看漲期權相聯繫的方法是由默頓引入的。R.C.Merton，“On Market Timing and Investment Performance：An Equilibrium Theory of Value for Market Forecasts，”Journal of Business，July 1981.

[7] 每一年都從正確的預測開始，然後用隨機數生成器把預測引向錯誤，從而使得對於牛市和熊市的預測正確率都是0.7。

[8] 注意，在式（24-7）中，當P=0時的投資者不會有收益。此時在市場間轉換等同於隨機地決定資產配置。