BUSINESS BOOKS

24.1　傳統的業績評價理論

24.1.1　平均收益率

我們在第5章第5.1節中定義了持有期收益率（HPR），並且解釋了算術平均與幾何平均的差異。設想我們根據一個投資組合5年內（即20個季度）的收益率評價其業績，可以用這些收益率的算術平均作為對下一季度收益率的估計，同時也可以用幾何平均收益率來進行估計。幾何平均收益率是指可以產生相同累積回報的20個季度的連續收益率。因此，幾何平均收益率可定義為：

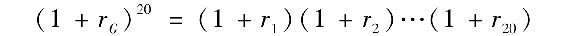
等式右側是1美元初始投資在5年觀察期內20個季度收益率累計複利的終值。等式左側是1美元初始投資以每季度r_G累計複利的終值。由此我們可以解出1+r_G：

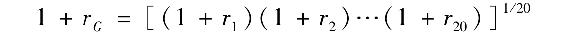
（注：這個公式給出季度收益率的幾何平均。當觀測區間長度為h年（本例中為1/4）年複利定義為1+r_GA=（1+r_Gh）^1/h。一般T個觀測值的h年化幾何平均收益是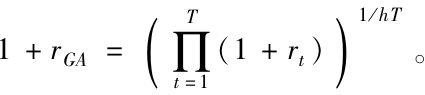在本例中，季度觀測值T=20，時間長度h=1/4年，1/hT=1/5，因此為了得到年化幾何平均，我們應該對5年投資期間收益開5次方根。）

在幾何平均中，每一期的收益率權重相同。因此，幾何平均收益率又被稱為時間加權收益率（time-weighted average）。

為了可以更好地理解後面的複雜問題，我們先看一個簡單的例子。考慮一隻股票，每年支付股利2美元，當前市價為50美元/股。假如你現在購買該股票，獲得2美元股利，然後在年底以53美元賣掉它，那麼你的收益率是：

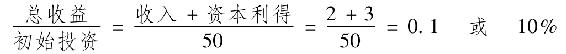
另一種計算收益率的方法是把投資轉化為現金流貼現問題。設r為收益率，它能使投資所創造的所有現金流的現值等於初始投資。在本例中，股票以50美元購得，年底產生的現金流包括2美元（股利）加53美元（出售股票）。因此，解方程50=（2+53）/（1+r），也得到r=10%。

24.1.2　時間加權收益率與美元加權收益率

如果我們的投資已持續了一段時間，且在此期間，我們還向投資組合注入或抽回了資金，那麼測算收益率就比較困難了。繼續看我們的例子，假如你在第1年年末購買了第二股同樣的股票，並將兩股都持有至第2年年末，然後以每股54美元的價格售出。

那麼你的總現金流為：利用現金流貼現法（DCF），令現金流入的現值與現金流出的現值相等，便可得到這兩年的平均收益率

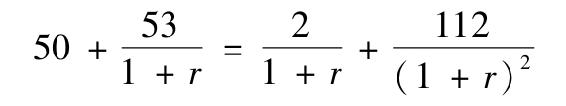
解得r=7.117%。

該值叫作內部回報率，也叫作美元加權收益率（dollar-weighted rate of return）。之所以稱為“貨幣加權”，是因為第二年持有兩股股票和第一年只持有一股股票相比，前者對平均收益率有更大的影響。

時間加權收益率（幾何平均）是7.81%：

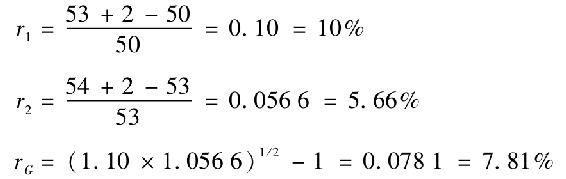
這裡的美元加權收益率比時間加權收益率要小一些。原因是第二年的股票的收益率相對要小，而投資者恰好持有較多股票。

概念檢查24-1

設XYZ公司在每年的12月31日支付2美元的股利，某投資者在1月1日以每股20美元的價格購入2股股票。一年後，即次年的1月1日他以22美元/股出售了其中一股；又過了一年，他以19美元/股出售了另一股。請分別計算這兩年投資的美元加權收益率及時間加權收益率。

24.1.3　美元加權收益率和投資表現

每個家庭都面臨著艱鉅的儲蓄目標，譬如孩子的教育和退休。這些目標中的一些能夠儲蓄避稅，譬如IRAS或者401（k）退休計劃和529大學費用計劃。這些賬戶本身和其他家庭資產賬戶分離。

家庭在選擇投資場所時有絕對的自由，並且家庭投資希望不時查看投資結果。他們應該怎麼做呢？答案很簡單，首先，家庭應該保留一份到期資金流入流出的電子賬單。在這個設置中，任何投資期間的美元加權平均收益將產生有效的到期回報率。^[1]

為了確保可以完成這項重要任務，更好地解決本章結尾習題1，可以看下文Excle應用專欄。

EXCEL應用：簡化的投資賬戶

假設一投資賬戶期初有10000美元，兩年間因存取款、股票分紅（未再投資）等原因賬戶資金進進出出如下表。表格展示了利用Excel的XIRR函數計算美元加權收益率。

Excel問題

1.如果2011年10月不出售股票S2，而是選擇繼續持有，投資的收益率將是多少？解釋兩種收益率的差異？

2.2012年3月時，投資者需要往賬戶中存入多少錢才能夠保證美元加權收益率為零？

24.1.4　風險調整收益

評估投資組合的業績，僅計算出其平均收益是不夠的，還必須根據風險調整收益，這樣，收益之間的比較才有意義。在根據投資組合風險調整收益的各種方法中，最簡單、最普遍的方法是將特定基金的收益率與其他具有類似風險的投資基金的收益率進行比較。例如，可以把高收益債券組合歸為一類，把增長型股票組合歸為一類，等等。然後確定各項基金的平均收益（一般是時間加權平均收益），並在各大類中根據對比情況（comparison universe）對各項基金的相對業績進行百分比排序。例如，在由100只基金組成的大類裡，第9名的管理者排序為90%，表示在本期評估內其業績比90%的同類競爭者要好。^[2]下文專欄報告了先鋒基金近期對於不同資產集合基準對比指數的修訂內容。

這些排名通常編製成表進行公佈，如圖24-1所示。該表彙總了1個季度、1年、3年和5年四個評估期的業績排名。圖中每個長方形最上面和最下面的線分別表示位於5%和95%的管理者的收益率，中間的三條虛線分別表示位於75%、50%（中位數）和25%的管理者的收益率。菱形代表某一特定基金的平均收益率，方塊代表市場基準指數的收益率，如標準普爾500指數。從菱形在格子中的位置就很容易看出該基金在對比情況下的經營業績。

圖24-1　同類對比（截至2010年12月31日）

在業績評估中，與其他相同投資基金的業績比較是第一步。然而，這些排名並不十分準確，甚至可能產生誤導。例如，在某個特定的環境下，一些經理可能更注重投資組合中的某一部分資產，這樣的投資組合特徵就不再具有可比性。例如，在資本市場中，某個經理可能更關注高β值或快速增長的股票；類似地，在固定收益證券的情況下，不同的經理關注不同的久期。上述情況表明，尋求更精確的風險調整方式是相當有必要的。

因此，兩種考慮風險調整的業績評估方法同時出現了，它們是均值-方差比值標準和資本資產定價模型（CAPM）。傑克·特雷納（Jack Treynor）^[3]、威廉·夏普（William Sharpe）^[4]和邁克爾·詹森（Michael Jensen）^[5]立即認識到了CAPM在評估經營業績上的特殊意義，隨即，學者掌握了一系列業績評估方法，學術界湧現出了大量對共同基金業績評估的研究成果。之後不久，市場上又出現了一些代理人，他們為投資組合管理人和其他客戶提供評級服務並收取固定回報。

華爾街實戰24-1　先鋒基金調整22只指數基金的基準

先鋒公司計劃將6只國際股票指數基金的業績跟蹤基準轉變為富時指數及16家美股和平衡指數基準。這一新的業績基準由芝加哥大學證券價格研究中心（CRSP）開發。長期來看，業績評價標準由當前MSCI到22只基金複合指數的轉變預期會為基金持有人節約大量成本。

“富時和CRSP綜合指數，全面覆蓋多個市場，滿足先鋒基金對市場業績基準‘最佳實踐’的要求，”先鋒首席投資官Gus Sauter如此說。

“我們同樣看重客戶的利益，因此與多家業績基準單位達成了許可協議，長期以更加低廉的成本增加指數基金和ETF持有人財富。”通常，為獲得授權需要付費給指數編制公司，而這一費用佔投資者持有指數基金和ETF費用的比例在不斷上升。Sauter指出，與富時和CRSP兩家指數編制公司的長期合作協議將保證該項成本未來相當確定。

2009年，CRSP與先鋒公司合作開發了多個新的可投資指數標的——CRSP系列指數。先鋒基金將成為首家追蹤CRSP業績基準的投資公司。CRSP系列指數不僅涵蓋了全美市場，還包括不同細分市值板塊和風格組合，採用獨特的市值加權方法，降低了股票在相近指數間變化引起的波動，分享在相同系列指數中的份額。這種方法在最大限度地提高風格純度的同時降低了指數交易量。

16只先鋒股票和指數平衡基金約有3670億美元總資產規模，將跟蹤CRSP基準，其中包括先鋒最大的指數基金，即1970億美元的先鋒全股票市場指數基金。基金和ETF股份（股票代碼：VTI）將從MSCI美國市場指數轉換為CRSP美國全市場指數。

基準的變化將包括22類基金份額，包括ETF。這一轉換可能會比較漫長，全部完成預計將歷經數月。先鋒美國股票指數基金將繼續跟蹤羅素和標準普爾基準，11只先鋒行業板塊股票基金繼續追蹤MSCI基準則不會做出調整。

資料來源：October 2，2012©The Vanguard Group，Inc.，used with permission.

儘管得到了廣泛的應用，各種風險調整的業績測度指標有著各自的缺點。更重要的是，它們的可靠性依賴於相當長期的一致管理、穩定的業績水平和富有代表性的投資環境（比如牛市和熊市）。但在實際操作中，我們往往需要在未能得到必要數據時就做出決定。

現在，我們列出一些經風險調整的業績測度指標，並考察其適用的條件。

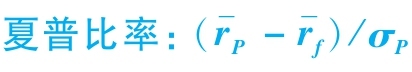　夏普比率（Sharpe’s ratio）是用某一時期內投資組合的平均超額收益除以這個時期收益的標準差。它測度了對總波動性權衡的回報。

（注：我們在r_P與r_f上加上橫線是要說明，由於在測度期無風險利率並不是不變的，因此我們要用樣本的平均值。類似地，我們也可以用樣本數據計算超額收益。）

　與夏普比率指標類似，特雷納測度（Treynor’s measure）給出了單位風險的超額收益，但它用的是系統風險而不是全部風險。

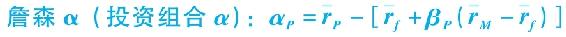　詹森α（Jensen’s alpha）是投資組合超過CAPM預測值的那一部分平均收益，它用到了投資組合的β值和平均市場收益，其結果即為投資組合的α值。

（注：在很多例子中，投資表現評價都是基於多因子市場假設形成的。比如，當使用法瑪-弗倫奇三因子模型時，詹森α是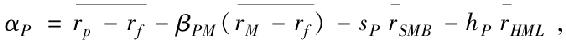其中s_P是SMB組合的加載，h_P是HML組合的加載。多因子的特雷納測度依然存在。）

信息比率：α_P/σ（e_P）　信息比率（information ratio）是用投資組合α除以該組合的非系統風險，也稱為“循跡誤差”。它測量的是每單位非系統風險所帶來的超額收益。非系統風險指原則上可以通過持有市場上全部投資組合而分散掉的那一部分風險。

晨星風險調整收益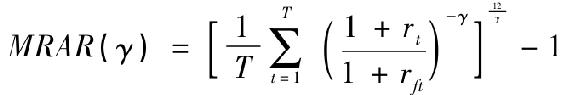：　晨星比率（Morningstar rating）是超額收益的調和平均，收益率是t=1，…，T的月度觀測值，γ衡量風險規避程度。高γ意味著對於風險的更多厭惡。對於共同基金，星晨比例中γ=2，這對於零散投資個體來說是較為合理的係數取值。MRAR可以被解釋為由γ作為風險厭惡係數的投資者無風險等價組合的超額收益。

（注：（1+r_t）（1+r_ft）數值近似於1加超額收益R_t。）

注：MARA測度是源於更復雜效用方程而不是第6章中均值方差方程的確定性等價的超額收益幾何平均。效用方程叫作常係數風險厭惡函數（CRRA）。當投資者擁有CRRA效用函數時，資本配置並不會隨著財富而增加。風險厭惡係數為A=1+γ，當γ=0（即A=1），效用函數正好是超額收益的幾何平均。

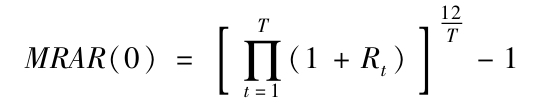
每一種指標都有其可取之處。由於各種經風險調整後收益指標在本質上是不同的，因此它們對於某一基金業績的評估並不完全一致。

概念檢查24-2

某特定樣本期內的數據如下：

請計算投資組合P與市場的下列業績評估測度指標：夏普比率、詹森α、特雷納測度、信息比率（假設此時國庫券利率為6%）。在哪種測度指標下，投資組合P的表現要比市場好？

24.1.5　業績的M²測度

雖然夏普比率可以用來評價投資組合的業績，但其數值的含義並不那麼容易解釋。比較“概念檢查24-2”中市場M和投資組合P的各項比率，可以得到S_P=0.69，S_M=0.73。這表明投資組合P的收益不如市場指數。但在夏普比率指標中，0.04的差異具有經濟意義嗎？我們常常比較收益率，但這些純數字形式的比率難以解釋。

格雷厄姆和哈維提出了改進的夏普比率指標，並由摩根士丹利公司的利婭·莫迪利亞尼（Leah Modigliani）和她的祖父、諾貝爾經濟學獎得主弗朗哥·莫迪利亞尼（Franco Modigliani）進行了推廣。^[6]他們的方法被命名為M²測度指標（表示莫迪利亞尼平方）。與夏普比率指標類似，M²測度指標也把全部風險作為對風險的度量，但是，這種收益的風險調整方法很容易解釋特定投資組合與市場基準指數之間的收益率差額。

M²測度指標的計算方法如下：假定有一個管理投資基金P，當我們把一定量的國庫券頭寸加入其中後，這一經調整的投資組合的風險就可以與市場指數（如標準普爾500指數）的風險相等。如果投資基金P原先的標準差是市場指數的1.5倍，那麼經調整的投資組合應包含2/3的基金P和1/3的國庫券。我們把經調整的投資組合稱為P*，它與市場指數有著相同的標準差（如果投資基金P的標準差低於市場指數的標準差，調整方法可以是賣空國庫券，然後投資於P）。因為P和市場指數的標準差相等，所以我們只要通過比較它們之間的收益率就可以來考察它們的業績。組合P的M²測度指標計算如下

【例24-1】M²測度

利用“概念檢查24-2”中的數據，P的標準差為42%，而市場指數的標準差為30%。因此，調整後的投資組合P*可以由30/42=0.714份的P和1-0.714=0.286份的國庫券組成。該組合的期望收益率為（0.286×6%）＋（0.714×35%）=26.7%，比市場指數的平均收益率少1.3%。所以該投資基金的M²_P測度為-1.3%。

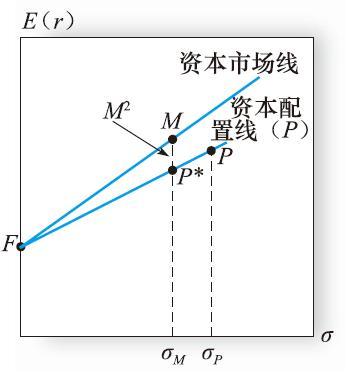
圖24-2　資產組合P的M²

圖24-2給出了M²指標的一個圖形表述。當我們把組合P與國庫券以適當比例組合的時候，就可以沿著P的資本配置線向下移動，直到調整後投資組合的標準差與市場指數的標準差相等。這時P*與市場指數的垂直距離（即它們期望收益率間的距離）就是M²_P測度。從圖24-2中可以看出，當投資基金P的資本配置線的斜率小於資本市場線的斜率時，即它的夏普比率小於市場指數時，P的M²測度就會低於市場指數。

注：從圖24-2中可以看出，實際上M²和夏普比率是直接相關的。用R代表超額收益，S代表夏普比率，圖中顯示R_P*=S_pσ_M，因此，

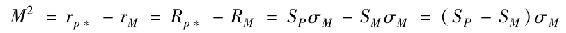
24.1.6　作為投資組合整體評價標準的夏普比率

假定珍妮·克萊斯構建了一個投資組合並持有了很長一段時間，在這期間她沒有調整該投資組合的構成。進一步假定所有證券以日計算的收益率具有相同的均值、方差及協方差。這些假設與現實相距甚遠。同時，它們對於理解傳統業績評估的缺點也是至關重要的。

現在我們試圖評估珍妮手中投資組合的業績。她是否選擇了好的證券？這個問題包含了三層意思。首先，“好的選擇”是和其他哪些選擇比較得出的？其次，在兩個明顯不同的投資組合之間進行選擇時，我們應該採用何種合適的標準來評價它們呢？最後，假如我們找到了合適的評價標準，是否存在一種方法，可以把該投資組合的基本獲利能力和隨機性的好運氣分開？

本書的前幾章主要就是在討論如何確定投資組合選擇標準。如果投資者的偏好可以用一個均值-方差效用函數來描述（如第6章中所述），我們就能得到一個相對比較簡單的評價標準。在第6章中，我們所用的效用函數為

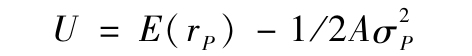
式中，A表示個體風險厭惡的係數。採用均值-方差的偏好選擇，珍妮就可以使夏普比率指標最大化，也就是使比率（［E（r_P）-r_f］/σ_P）最大化。在第7章中我們談到，這種評價標準會讓投資者選擇有效邊界切點的投資組合。現在擺在珍妮面前的問題就變成了如何找到具有最大夏普比率的投資組合。

24.1.7　兩種情景下合適的業績測度方法

對珍妮的投資組合選擇做出評估前，首先要確定該投資組合是不是她的唯一的投資組合。如果不是，我們就還需要知道她其他的投資組合。投資組合評價標準的正確與否在很大程度上取決於該組合是不是她所有的投資工具，或者只是她全部財富中的一部分。

該投資組合代表珍妮所有的風險投資　在這種最簡單的情況下，我們只需確定珍妮的投資組合是否具有最大的夏普比率。按照如下三步進行分析。

（1）假設證券的過去業績就是其未來業績的代表，這意味著證券在珍妮持有期間所實現的收益與珍妮預期證券未來收益的均值、協方差等特徵是相同的。

（2）如果珍妮選擇消極策略，如持有標準普爾500指數的投資組合，確定珍妮應選擇怎樣的投資組合作為標杆。

（3）把珍妮投資組合的夏普比率值與最佳投資組合的夏普比率值進行比較。

總的說來，當珍妮的投資組合就是她所有的投資時，與之比較的標準就應是市場指數或另一個特定的投資組合。業績評估就是把實際的投資組合與所選定的標杆組合的夏普比率指標進行比較。

珍妮的投資組合只是她所有投資資金中的一部分　如果珍妮是公司的財務主管並管理著公司的養老基金，那麼這種情況就可能發生了。她現在可以把整個基金劃分為幾個部分，然後分給一些投資組合經理。但她為了能重新調整基金的投資去向以期提高今後的整體業績，必須評價每一位投資組合經理的業績。正確的業績評估指標應該是什麼呢？

儘管α值是衡量業績的基礎，但僅僅這一個指標不足以確定P對組合的潛在貢獻。下面的討論說明了為什麼在這種情況下，特雷納測度是最為合適的標準。

夏普比率是平均超額收益（回報）和總標準差（投資組合總風險）的比值。它是資本市場線的斜率。然而，當僱用許多資產管理人進行組合管理時，非系統性風險被大大分散，系統性風險成為風險的相關測度。最合理的衡量表現的矩陣是由平均超額收益和β比值構成的特雷納矩陣（因系統的SD=β·市場SD）。

根據相關數據得到表24-1，並據此結果得到圖24-3。注意，我們是在期望收益-β平面（而非期望收益-標準差平面）上描出P、Q兩點，這主要是因為我們假定P、Q只是總基金中眾多子投資組合元素中的兩個，因此，非系統風險就在很大程度上得到分散，最後只剩下β作為其合適的風險測度指標。圖中證券市場線（SML）與P、Q的距離就是α_P與α_Q的值。

如果我們把w_Q的比例投資於投資組合Q，那麼國庫券中的投資比例即為w_F=1-w_Q，於是最終投資組合Q*的α值和β值就會由Q的α值、β值及比例w_Q來決定

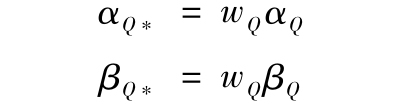
表24-1　投資組合業績

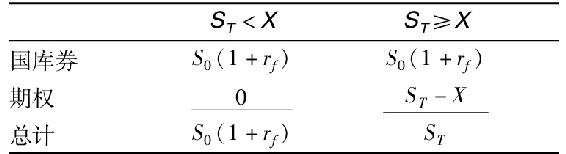
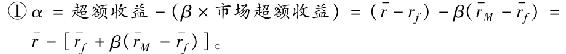
因此，所有如此生成的投資組合Q*就都可以在連接原點與Q點的直線上找到。我們把這條線稱為T線，其斜率為特雷納測度。

圖24-3也顯示了投資組合P的T線。P的T線顯然更陡，儘管它的α值較低，但它應該是一個更佳的投資組合。在任意給定的β值下，P與國庫券的混合投資組合會比Q與國庫券的混合投資組合有更大的α值。

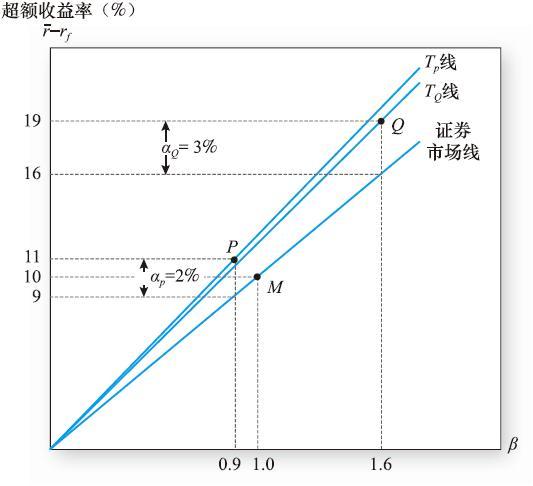
圖24-3　特雷納測度

【例24-2】令β值相等

假設我們把Q與一定比例的國庫券混合組成投資組合Q*，並使該組合的β值與組合P的β值相等。解出混合比例w_Q

β_Q*=w_Qβ_Q=1.6w_Q=β_P=0.9

w_Q=9/16

因此，投資組合Q*的α值為

α_Q*=9/16×3%≈1.69%

它顯然小於P的α值。

換句話說，在這種情況下，該投資組合T線的斜率就是其合適的業績評估標準。投資組合P的T線的斜率T_P可按下式計算

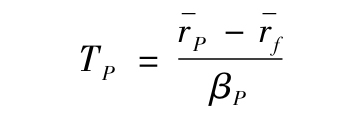
像M²測度一樣，特雷納測度也是一個百分比。當你把市場超額收益從特雷納測度指標中減去後，你將會得到圖24-3中的T_P線收益與β=1時的證券市場線收益之差。我們把這個差稱為特雷納平方，或T²測度（類似於M²）。但請注意，正如夏普比率與特雷納測度不同，M²和T²也是不同的。它們可能對相同的投資組合得出完全不同的排序。

24.1.8　α在業績度量中的作用

掌握了一些代數知識之後，就可以得出前面介紹過的各種業績度量方法之間的關係，如下表所示。

①r表示市場組合與P組合之間的相關係數，r＜1。

因為所有模型都要求α為正，所以α在業績評估中使用得最為廣泛。然而。對夏普比率來說，僅α為正並不能保證更好的組合業績，因為利用證券的誤定價意味著背離了分散化投資的原則，而這會引發一些成本。共同基金可以在增加標準差從而使夏普比率下降的情況下獲得正α值。

24.1.9　業績度量實例

在討論了度量業績的各種可行標準後，我們還須解決一個統計學的問題：我們能夠利用事後的數據來評價事先決策的質量嗎？在對這個問題集中討論之前，先讓我們看一下珍妮的投資組合在過去12個月中的收益率情況。表24-2列出了珍妮的投資組合P和她另一種可能的選擇投資組合Q，以及市場指數M的每月超額收益。表24-2的最後幾行是樣本的均值和標準差。從這些數字以及P與Q對M進行的線性迴歸中，我們得到了進行業績評估所必需的數據。

表24-2　投資組合P、Q和基準指數M12個月中的超額收益　（%）

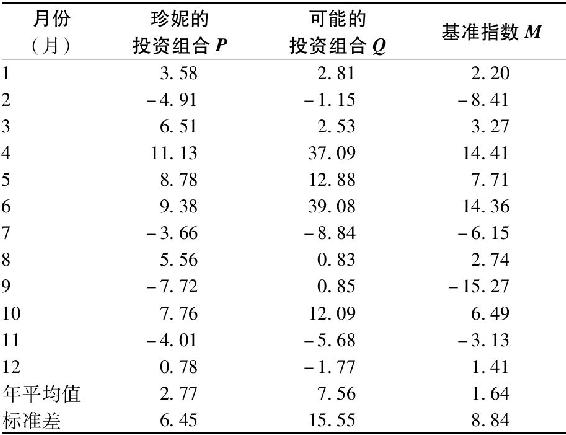
表24-3　業績評估數據

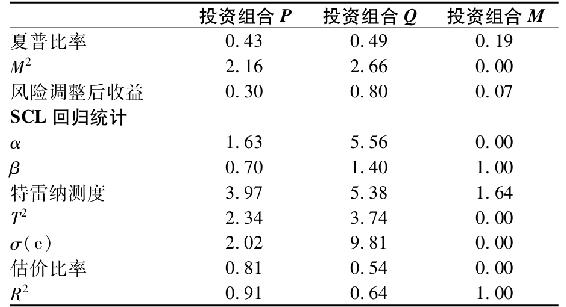
表24-3中所列的業績評估數據顯示，投資組合Q比投資組合P更具冒險性，因為Q的β值（1.4）要明顯地高於組合P的β值（1.40比0.70）。另外，從剩餘標準差來看，投資組合P似乎要分散得更好一些（P為2.02%，Q為9.81%）。由於兩個投資組合都具有較大的夏普比率（即正的M²測度）、正的α值以及更高的風險調整後收益，投資組合P、Q的表現都要好於市場指數標準。

那麼，從上述指標來看，到底哪一個投資組合更具吸引力呢？如果P或Q是珍妮的所有投資基金，Q應該更被看好，因為Q具有更高的夏普比率（0.49∶0.43）和更大的M²測度（2.66%∶2.16%）。對於第二種情況，即P、Q只是珍妮所有投資中的一部分時，Q也更勝一籌，因為它有更高的特雷納測度（5.38∶3.97）。然而，當把P、Q這兩種積極投資策略與消極的市場指數投資相結合時，由於P的信息比率高（0.81∶0.54），因此投資組合P要優於投資組合Q。所以，這個例子說明證券的業績評估在很大程度上依賴於該證券組合在投資者所有資產中的作用與地位。

但是，上述分析只建立在短短12個月的數據之上，因此我們不能完全確定結論是否可靠。其實就算更長時間段的樣本觀察值也可能不足以使決策更清晰，因為這本身就是一個需要更加深入探討的問題。計算這些組合測度的模型可以在“在線學習中心”上查找。

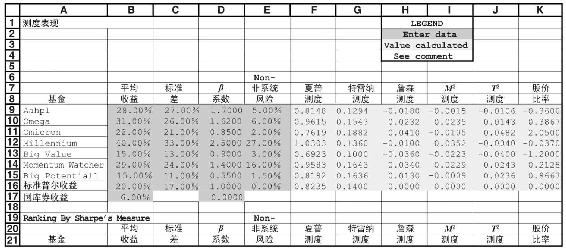
Excel應用

業績測度

下表計算了該節討論的所有的業績測度。按照選擇的不同標準，你可以看到相對排名次序是如何不同的。該表可以從“在線學習中心”（www.mhhe.com/bkm）獲得。

Excle問題

1.驗證電子表格中的基金表現測度。將表現情況排序並確定不同測度指標下的排序是否一致。這些結果說明了什麼？

2.如果考慮將資產組合全部投資於風險資產，你會選擇哪隻基金？如果你要選取一隻最近投資市場指數的基金加入組合，你會選擇什麼？

24.1.10　業績操縱和風險調整收益

目前表現評價指標都基於每個時期收益率獨立且來自同一分佈的假設，即統計特性表現為收益率獨立同分布。當薪酬與表現掛鉤的管理人違背體系隨意操作時，這個假設會從內部瓦解。即便對投資者有害，管理人也會使用能夠改進表現衡量體系的策略。長此以往，管理人薪資也可能會與組合獲利表現相脫鉤。

管理人可以在給定投資期間內影響衡量表現的指標，因為他們可以觀察到收益來源並據此相應調整組合。一旦這樣，近期收益率將很大程度上取決於最初的收益率。

英格索、施皮格爾、高特斯曼和韋爾奇^[7]展示了本章衡量投資表現被操縱的測度指標。唯一的特例是衡量表現操縱情況的測度指標晨星風險調整收益率。就像我們現在使用夏普比率的邏輯一樣，晨星風險調整收益率模型的細節推導具有挑戰性，但邏輯很直接。

正如第6章分析資本分配中減少無風險資產投資（借貨）並不會影響組合的夏普比率，即夏普比率在風險資產中所佔比例y是相同的，因為保持夏普比率不變，超額收益、風險溢價以及標準差均和y成正比。但是如果y產生變動呢？如果在觀察到投資表現之前決定改變投資槓桿率，夏普比率不受影響，因為兩部分收益率不相關。

設想管理人已經在評價期內，雖然實現的超額收益在前期評價中並不知道，未來持續收益的分佈也和過去相同，但整體夏普比率將會是某些（複雜的）前期已知和後期未知收益的平均。在後期操作中，提高槓杆將會增加平均表現的權重，因為不論好壞槓桿都會放大收益。因此，如果早期收益率表現不好^[8]，管理人希望在之後的時間裡增加槓桿。相反地，期初收益表現較好將會要求降低槓桿，增加期初時期的收益權重。如果期初收益非常好，管理人會將幾乎全部組合投入無風險資產中。這個策略將導致前期和後期收益率負相關。

平均看來，投資者無法跑贏這類策略。槓桿套利效用是遞減的，且它只有利於管理人，因為這一策略允許他們在觀察到最初表現後在整個評價期內調整投資權重。^[9]因此，投資者將會禁止或者至少打消追逐這類策略。然而，當僅有一個表現測度指標的時候，投資表現就是幾乎不可能被操縱的。

一個可以證明操縱表現的測度指標（MPPM）必須滿足四個要求：

（1）測度指標應該產生單值的分數可以進行排序。

（2）分數不依賴於組合的美元價值。

（3）無信息的投資者不應該期待與基準組合相背離來提升預期分數。

（4）測度應該與標準金融市場均衡條件相一致。

英格索等證明了晨星RAR滿足這些要求，且實際上是可以證明操縱投資表現的測度指標（MPPM）。有趣的是，起初晨星推出MRAR的目的並不是MPPM，它只是嘗試適應投資者的常係數風險厭惡函數。

圖24-4a展現了基於統計模擬100個組合的夏普比率和MRAR散點圖。對於組合36%的超額收益率是隨機生成的，年預期收益7%，標準差在10%~30%變化。因此，這些擬合的共同基金真實夏普比率在0.7和0.23之間，均值為0.39。因為抽樣變異，實際模擬中的100個夏普比率和總體參數有很大的不同。夏普比率在-1.02和2.46間波動，平均值為0.32。100個MRAR在-28%和37%之間波動，均值為0.7%。兩個測度指標相關係數為0.94，說明夏普比率能很好地追蹤MRAR，而散點也顯示擬合點均緊密地分佈在一條斜率為0.19的直線周邊。

圖24-4b（和圖a一樣是散點圖）闡述了當最初組合投資表現被觀察到，並允許槓桿變化操縱的效果。特別是在評估的中間36個月期間。^[10]操縱的效果對於擁有極端價值組合的影響很顯著。對於最初MRAR為正且較高的組合，向無風險投資轉變可以防止前期高夏普比率被稀釋或者在後期出現反轉。對於最初MRAR為負擔數值較高的組合，當槓桿率增加，我們會看到兩種效應。首先，MRAR因為高槓杆效果適得其反相對於圖a使得MRAR看起來更糟糕。與此相比，夏普比率在圖a中看起來更好。一些夏普比率由負轉正，然而其他看起來並沒有更糟（因為後期標準差增加降低了負夏普比率的絕對價值）。

圖24-4b中數據數量化顯示出夏普比率的改進。相反，MRAR卻由正值減少到年收益-2.74%，而前後兩期平均收益的相關性也從正變為負。這些均是由於槓桿從1.0增加為1.39所致。^[11]

晨星2002年引入MRAR這個指標，它和那些管理人有極大自由和動機進行操縱的對衝基金特別相關。進一步的討論可以參見第26章。我們希望未來MRAR測度能成為標準業績表現統計量，幫助投資者篩選那些擁有較好投資決定權把控的管理人。

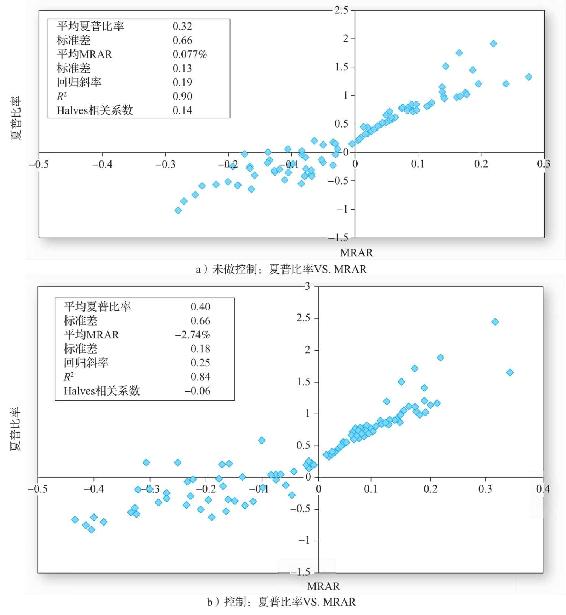
圖24-4　MRAR計分與夏普比率在有控制與無控制下的相關性

24.1.11　已實現收益與期望收益

在對某個投資組合進行評估時，評估者其實並不瞭解投資組合管理者對該投資組合最初的預期，當然更不清楚這些預期是否合理。他只能在事實發生之後觀察投資組合的業績，同時還希望隨機干擾不會掩蓋投資組合的真實收益能力。但事實上風險資產的收益是“白噪聲”的，這無疑會使這個問題複雜化。為了避免這種錯誤，我們就必須定出該種業績評估指標的“顯著性水平”，以確定其是否可靠地反映了組合的實際獲利能力。

假設現有一個投資組合管理者喬·達特，如果其資產組合的月α值為20個基點，那麼顯然他每年會有2.4%的α值（未計複利）。我們還假定喬的投資組合的收益具有固定的均值、β值和α值。這確實是相當嚴格的假設，但其實它們和一般情況下業績指標的處理前提是一致的。我們再假定在評估期內該投資組合的β值為1.2，每月殘差的標準差（非系統風險）為2%，如果市場指數的標準差為每月6.5%（每年22.5%），那麼喬的投資組合的系統方差為

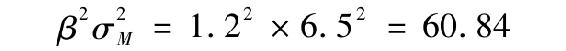
於是該投資組合和市場指數之間協方差的相關係數就為

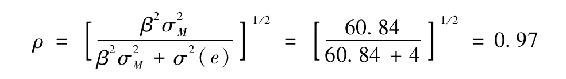
這個數字表明該資產是高度分散化的。

為了從證券市場線上估計喬的投資組合的α值，我們把投資組合的超額收益對市場指數進行迴歸。假設我們通過線性迴歸幸運地估計出了方程的參數，那麼對N個月內證券市場線的估計為

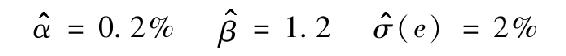
然而評估者在做線性迴歸時根本不知道真實數據是多少。因此，他還必須計算α估計值的t統計量，從而確定他是否應拒絕該投資組合α值為0的原假設（也就是該投資組合並沒有更出色業績的假設）。

在證券市場線迴歸中α估計值的標準差近似為

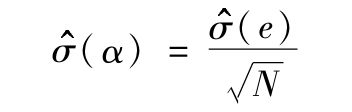
這裡N是樣本數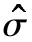，（e）是樣本非系統風險的估計值。α估計值的t統計量於是就應為

假定我們要求的顯著性水平是5%，在這個顯著性水平下，t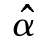（）就應為1.96（若N能足夠大）。把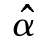=0.2和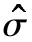（e）=2代入式（24-2），解得N值為：

這說明什麼？喬確實是一位才能出眾的分析師，使用的例子是他喜歡的假設方式，即遠離那些令人頭痛的統計難題，假設參數在長期內不會改變，而且樣本期內的“表現”也無可挑剔，迴歸估計結果全部令人滿意。但這仍需要喬花去他一生的工作精力來證明其具有的出色能力。我們不得不得出結論，在實際工作中，統計數據的干擾性問題使得業績評估工作變得尤為困難。

除上述難題外，由於基金經理的平均任期只有4.5年，這更加劇了業績評估的不準確性問題。也就是說，就算你非常幸運地找到了一個對其未來表現非常有信心的基金，但它的經理也差不多或者已經離職了。華爾街實戰24-2討論了這個問題。

華爾街實戰24-2　是否應追隨基金經理

投資共同基金的初衷在於讓專業人士幫你挑選股票和債券。但很多時候，天有不測風雲——經理可能會退休、跳槽甚至死亡。投資者決定購買共同基金很大程度上取決於該基金經理的投資記錄，因此這種變化往往會讓人不安。

在經理離開後，事態發展並無定數。但是，事實證明經理對於基金表現的真實貢獻往往被高估了。比如，晨星公司研究比較了1990~1995年有過經理更換和經理沒有變動的基金表現，五年後的2000年6月，前五年間業績最佳的基金繼續超越了其他同行——無論這些基金有沒有換過經理。而在前五年表現糟糕的基金不論是否更換經理，業績依然不佳。共同基金公司無疑會繼續推出明星經理並且宣傳他們過去的投資記錄，但投資者應當更加關注於基金本身的表現。

基金經理們過去三五年的投資記錄促進了基金公司的發展。但是僅僅幾年的業績數據很難成為出眾才智的有力證據。想要在統計上有顯著性，一個經理至少要有十年以上的投資記錄。

共同基金行業就像一個旋轉木馬，上面坐著不同的基金經理任你挑選，但是投資者不必擔心。從設計上來說，基金經理離開後幾乎不會對共同基金產生影響。這是因為為了降低風險和一系列困擾，共同基金通常是由各自管理著一小部分資產的股票挑選人團隊共同管理的，並非由單獨一個經理和他的副手管理。與此同時，即使是所謂明星經理身邊也有一大批研究人員和分析師，他們充當了和上報紙頭條上的經理同等重要的作用。

別忘了，即使經理離開了，投資還在那裡，持有的基金並沒有改變。這和一家公司的CEO離開引起股價下跌是不同的。最好的做法就是密切關注一切可能影響基金基本投資質量變化的因素。

進一步說，不要低估了基金公司“經理板凳”（managerial bench）的寬度和廣度，通常來說，大型的基金公司都有大型人才儲備。他們也清楚當經理變動時，投資者傾向於離開基金。

最後，對於擔心管理人變動的投資者，這裡有一個解決方案——指數基金。指數基金並不依賴於明星經理，這種共同基金通過購買股票和債券來跟隨某個目標指數，如標準普爾500指數。在這種情況下，經理是否離開不再重要。與此同時，指數投資者也就省去了當經理離開時撤離基金所要繳納的稅款。更重要的，指數投資者不需要為明星經理高昂的工資買單。

資料來源：Shauna Carther，“Should You Follow Your Fund Manager？”Invesopedia.com，March 3，2010.Provided by Forbes.

[1] Excle函數XIRR允許你在任何日期輸入總數。給出初始值、期間不同日期的現金流（付款代表正現金流，提款代表負現金流）和終值，Excle函數可以計算兩個日期間的IRR值。

[2] 前面的章節（尤其是第11章講述有效市場假說時）中，我們對積極管理投資組合時的業績能否超過消極指數業績進行了檢驗。為此，我們研究了部分共同基金樣本的α值分佈。我們發現，從這些樣本中得出來的任何結論都存在存活者偏差，因為如果基金破產了就將被踢出樣本組。在本章中，重點討論單個基金業績的評估方法。當選準一隻基金後，就不存在存活者偏差了。但是做比較時的樣本組一定要排除存活者偏差，一個只由倖存基金組成的樣本組必然比基準組業績更好，而相對錶現比任何個別基金更差。

[3] Jack L.Treynor，“How to Rate Management Investment Funds，”Harvard Business Review 43（January-February1966）.

[4] William F.Sharpe，“Mutual Fund Performance，”Journal of Business 39（January 1966）.

[5] Michael C.Jensen，“The Performance of Mutual Funds in Period 1945-1964，”Journal of Finance，May 1968；and“Risk，the Pricing of Capital Assets，and the Evaluation of Investment Portfolios，”Journal of Business，April 1969.

[6] John R.Graham and Campbell R.Harvey，“Market Timing Ability and Volatility Implied in Investment Advisors′（24-1）Asset Allocation Recommendations，”National Bureau of Economic Research Working Paper 4890，October 1994.該論文中關於風險調整收益的部分最終發表於“Grading the Performance of Market Timing Newsletters，”Financial Analysts Journal 53（November/December 1997），pp.54-66.Franco Modigliani and Leah Modigliani，“Risk-Adjusted Performance，”Journal of Portfolio Management，Winter 1997，pp.45-54.

[7] Jonathan Ingersoll，Matthew Spiegel，William Goetzmann，and Ivo Welch，“Portfolio Performance Manipulation and Manipulation Proof Performance Measures，”Review of Financial Studies 20（2007）.

[8] 那些不能加槓桿的管理人會轉而投資高β股票。如果這是個廣泛現象，就可以解釋為什麼高β股票相對於低β股票定價更高。

[9] 降低操縱行為的方法是頻繁的評價組合表現，但同時也會降低測度指標的統計精確性。

[10] 為了讓練習更貼近實際，槓桿率設定為2（資產負債率為1）。

[11] 100個基金中，槓桿比率在38個投資組合中降低。至少1/7的組合槓桿率增加，1/12的組合槓桿率不僅出現增加，而且在不考慮市值時會增加更多。