e1 Zvi Bodie 投資學 v10
23.5 商品期貨定價
商品期貨的定價基本上與股票期貨一樣。不過有一點不同，那就是商品的持有成本，尤其是易損商品，比金融資產的持有成本大得多。一些期貨合約的標的資產並不能簡單地“持有”或保存在資產組合中，如電力期貨。此外，一些商品的現貨價格有明顯的季節性變化，這也會影響商品期貨的價格。
23.5.1 有儲存成本時的定價
除了利息費用外，商品的持有成本還包括儲存成本、保險成本和存貨毀損備抵。為了確定商品的期貨價格，讓我們再考慮一下前面提到的那種同時持有資產與該資產期貨空頭的套利方法。這裡我們用PT表示T時商品的價格，另外簡單起見，假定所有的非利息成本為C，在合約到期時，T一次性付清。這些費用出現在最終的現金流中。因為市場不允許存在套利機會，所以這種淨投資為零的無風險策略的最終現金流，應該為零。
如果現金流為正，按照這種方法不需要任何投資就可以保證得到利潤。如果現金流為負，採取相反的步驟仍可以獲得利潤。實際上，反向操作需要賣出商品，這是不常見的，不過只要合理地考慮了儲存成本就仍是可行的。這樣[1]，我們可以得到
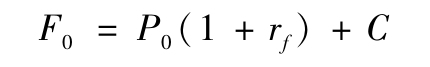
最後，如果我們令c=C/P0，即c是以百分比形式表示的持有成本，我們就可寫出
這就是一個包含儲存成本的1年期的期貨平價關係。將式（23-3）與上一章股票平價關係式（22-1）做比較，你會發現它們非常相似。實際上，如果我們把持有成本視為“負股利”的話，這兩個公式就是完全相同的。這是一種很直觀的解釋，因為商品持有者不是收到股利收益d，而是支付儲存成本c。顯然，該平價關係只是我們以前推導出的平價關係的簡單拓展。
雖然我們稱c為商品的持有成本，更一般地我們也可以把它解釋為淨持有成本，即持有成本扣除來源於持有存貨的收益。例如，持有存貨的部分——“便利收益”便是可以防止缺貨，以免延誤生產或失去客戶。
必須說明的是，式（23-3）是在假設資產可以被買進並儲存的前提下得到的，因此它只適用於現在需要儲存的商品。有兩類商品不能儲存：一類是儲存在技術上是不可行的，如電力；另一類是出於經濟原因不應儲存的商品，例如現在就買進一種農產品，而計劃3年後才最終使用是非常愚蠢的。事實上，最好的辦法是等到第3年收穫後再去購買，這樣就可以避免儲存成本。而且，如果3年後產量與今年相當的話，那你也能以與今年差不多的價格買到它。等到3年後再去購買，你節省了利息費用和儲存成本。
因為在收穫期間儲存商品是昂貴的，所以式（23-3）不適用於跨越收穫時期的持有情況，也不適用於那些“應時”的易腐爛商品。黃金是一種可儲存商品，所以它的期貨價格隨著期限的延長而穩步上升，而小麥期貨價格卻是季節性的：3~7月新收穫小麥上市時它的期貨價格會明顯回落。
圖23-9是一種農產品價格典型的季節性走勢。顯然，這種走勢與股票或黃金等金融資產的價格走勢有很大的不同，後者不會有季節性的價格變化。金融資產具有價格是因為持有它們能夠獲得期望收益。相反，農產品價格在每次收穫時都會大幅下跌，這就使得跨收穫期儲存農產品常是無利潤的。
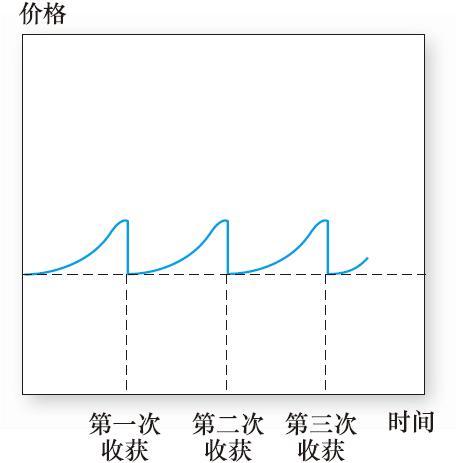
圖23-9 農產品價格典型的季節性走勢，價格經通貨膨脹調整
跨季的期貨定價需要一種不同的方法，該方法不是建立在跨收穫期儲存的基礎之上。我們使用風險溢價理論和貼現現金流（DCF）分析來代替一般的無套利約束。
概念檢查23-8
儘管受到資本約束，人們還是希望購買並“存儲”股票，但人們不願去購買並存儲大豆，那麼股票價格走勢與大豆價格走勢之間的什麼特性差異導致了這樣的結果？
23.5.2 商品期貨的貼現現金流分析
給定未來某一時刻商品現貨價格的當前預期和那個價格風險特徵的測度指標，我們就可以測量未來某一時刻得到該商品的權利的現值。我們簡單地根據資本資產定價模型與套利定價模型來計算恰當的風險溢價，然後用風險調整後的利率對預期的現貨價格進行貼現，見下面的例子。
【例23-8】商品期貨定價
表23-3列出了一系列商品的β係數，例如，橘汁的β係數估計值為0.117。如果當前國債的利率為5%，歷史上市場風險溢價為8%，那麼由資本資產定價模型計算出來的橘汁的合理貼現率為
5%+0.117×8%=5.94%
表23-3 商品的β係數
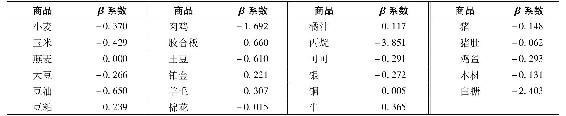
資料來源：Zvi Bodie and Victor Rosansky，“Risk and Return in Commodity Futures，”Financial Analysts Journal 36（May-June 1980）.Copyright 1980，CFA Institute.Reproduced from the Financial Analysts Journal with permission from the CFA Institute.All rights reserved.
如果預期6個月後的橘汁現貨價格為每磅[2]1.45美元，那麼6個月後購買橘汁的價格的現值就為
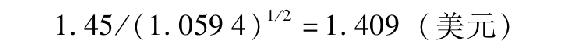
那麼，合理的橘汁期貨價格是多少呢？這份合約要求最終交割橘汁時按期貨價格執行。我們剛才已經得出橘汁的現值是1.409美元，它應該等於支付橘汁的期貨價格的現值。協議在6個月後支付F0美元的現值是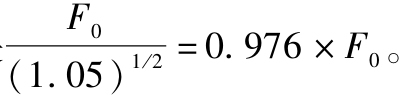
（注意，貼現率是無風險利率5%，因為承諾的支付是固定的，與市場條件無關。）
使承諾支付F0的現值與承諾收到商品的現值相等，我們就可以得到
0.976F0=1.409美元
即
F0=1.444美元
確定合理期貨價格的一般規律是，使未來支付F0的現值與即將收到商品的現值相等，因此我們有
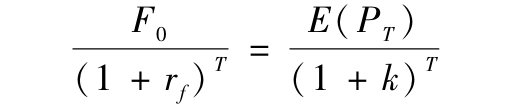
即
式中，k為商品的必要收益率，它可以從資產市場均衡模型，如資本資產定價模型中得到。
概念檢查23-9
假定橘汁的系統性風險增加，而在時刻T的期望價格不變。如果預期的現貨價格不變，那麼期貨價格是否發生變化？如何變？你答案背後的直覺是什麼？
注意，式（23-4）與現貨-期貨平價關係完全一致。例如，用式（23-4）計算一種不付股利股票的期貨價格。因為股票的全部收益都是資本利得，所以它的期望資本利得率應該等於它的必要收益率k。因此，股票的期望價格應該是它的當前價格乘以（1+k）T，或E（PT）=P0（1+k）T，把它代入式（23-4）得到F0=P0（1+rf）T，這與平價關係完全相同。
[1] Robert A.Jarrow and George S.Oldfield，“Forward Contracts and Futures Contracts，”Journal of Financial Economics 9（1981）.
[2] 1磅=0.4536千克。