BUSINESS BOOKS

23.3　利率期貨

對衝利率風險

同股票管理人一樣，固定收益證券管理人有時也想對衝市場風險，即來自整個利率期限結構的變動。例如，考慮到以下這些問題。

（1）一個固定收益證券管理人持有一個已獲得相當可觀的資本利得的債券組合。她預計利率會上升但是不願意出售她的資產組合，並以一個短久期債券組合來替代該組合，因為這樣做會帶來巨大的交易成本和資本利得的稅收。她願意對衝她的風險敞口，以規避利率上升的風險。

（2）一家公司計劃公開發行債券。它認為目前是發行的好時機，但是因為一直存在SEC註冊的滯後期，在3個月內公司不能發行債券。公司希望對衝收益率的不確定性，這樣它就能全部賣掉債券。

（3）一個養老基金下個月將收到一筆很大的現金，計劃將其投資於長期債券。考慮到時利率下降的可能性，基金希望能夠把長期債券的收益率鎖定在當前水平。

在以上每個案例中，投資管理人都希望對衝掉利率的不確定性。為了說明操作程序，我們集中研究第一個案例，並假設資產組合管理人持有1000萬美元的債權資產組合，其修正久期為9年。^[1]如果像所擔心的那樣，市場利率真的上升了，債券組合的收益率也會上升，比如說10個基點（0.10%），基金就會有資本損失。回顧第16章的內容，資本損失的百分比是修正久期D*與資產組合收益率變化的乘積。因此，損失為

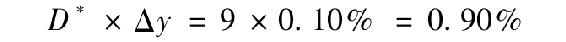
也就是90000美元。這表明，收益率變化1個基點，未保護頭寸的價值將變化9000美元。這個比率被市場人士稱為基點價值（price value of a basis point），記為PVBP。PVBP代表資產組合美元價值對利率變化的敏感性。我們可以用公式表示如下

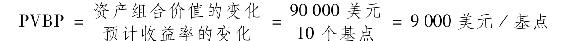
對衝這個風險的一種方法是建立利率期貨合約的抵消頭寸。國債面值為100000美元，票面利率為6%，期限為20年。因為具有不同的票面利率和期限許多債券都可替代國債用於結算，實際中合約的交割標準相當複雜。我們假設用於合約交割的債券已經確定，其修正久期為10年，當前面值100美元的債券期貨價格為90美元。因為合約要求交割100000美元面值的債券，所以合約乘數是1000美元。

有了以上數據，我們就可以計算期貨合約的PVBP。如果交割債券的收益率上升10個基點，債券價值將下降D*×0.1%=10×0.1%=1%。期貨價格也將下跌1%，從90降到89.10。^[2]因為合約乘數是1000美元，所以每份合約空頭的收益為1000美元×0.90=900美元。因此，期貨合約的PVBP為900美元/10個基點，即收益率變化1個基點為90美元。

現在我們可以方便地計算出對衝比率

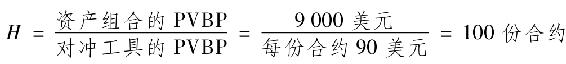
概念檢查23-5

假設債券組合增大1倍，變為2000萬美元，修正久期為4.5年。證明對衝要用的國債期貨合約的數量與剛才所計算的一樣，為100份合約。

這樣，100份國債合約就可以抵消資產組合在利率風險上的風險敞口。

注意，這是市場中性策略的又一個例子。例23-5中闡述了股票對衝策略，股指期貨可被用來使得資產組合的β為零。在這個例子中，我們用國債期貨使得債券頭寸的利率風險敞口為零。經過對衝的債券頭寸的久期（或PVBP）為零。風險來源不同，但對衝策略在本質上是相同的。

雖然對衝比率很容易計算，但是實際中的對衝問題非常困難。在我們的例子中，我們假設國債與債券組合的收益率變動是完全一致的。雖然不同債券工具的利率有相同的變化趨勢，但不同類別的債券之間還是存在相當大差異的。如圖23-5所示，從長期來看，長期公司債券與10年期國債的利差具有相當大的波動。只有兩類固定收益債券的利差是常數（或者至少可以精確預測），也就是兩類債券收益率變動相等時，我們的對衝策略才是完全有效的。

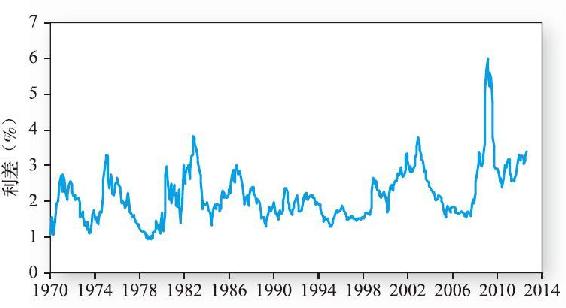
圖23-5　10年期國債與Baa級公司債券的利差

這個問題突出了這樣一個事實，大多數對衝策略實際上是交叉套期（cross-hedging），意味對衝工具與要被對衝的資產不屬於同一類資產。兩種資產的價格或收益率存在差別，因此在這個意義上，對衝將不夠完全。交叉對衝可以消除未受保護資產組合的總風險的一大部分風險，但是你需要意識到它們與無風險頭寸相比仍有明顯的距離。

[1] 回憶一下修正久期的概念D*，它與久期D相關，計算公式為D*=D/（1+y），其中y是債券的到期收益率。如果債券每半年付一次利息，y就應當是半年的收益率。簡單起見，我們假設每年付一次息，把y作為有效的年化收益率。

[2] 這裡假設期貨價格與債券價格完全同比例變動，通常，也幾乎如此。