e1 Zvi Bodie 投資學 v10: 23.1 外匯期貨

e1 Zvi Bodie 投資學 v10

23.1　外匯期貨

23.1.1　市場

貨幣之間的匯率不停地變化，並且通常比較劇烈。這種變化是所有從事國際商務的人都關心的。例如，一個在英國銷售貨物的美國出口商收到以英鎊支付的貨款，而這些英鎊的美元價值取決於付款時的即期匯率。直到付款那天，這位出口商將一直面臨匯率風險。這種風險可以通過外匯期貨或遠期市場進行套期保值來避免。例如，如果你將在90天內收到100000英鎊，你現在可以在遠期市場上賣出英鎊遠期，把匯率鎖定在與今天遠期價格相同的匯率上。

外匯的遠期市場一般是非正式市場，它只是一個允許客戶建立遠期合約在將來以當前協議的匯率買賣貨幣的經紀人與銀行之間的交易網絡。銀行間的外匯市場是世界上最大的金融市場之一，許多有足夠信譽的大交易商是在這裡而不是在期貨市場上做外匯交易。與期貨市場不同，遠期市場上的合約是非標準化的，每一份合約都是單獨協商定價，而且也不存在期貨市場中的盯市。外匯遠期合約都是到了到期日才執行。市場參與者需要考慮交易對手風險，即合約對方可能因為價格對他不利而不再履行合約責任的風險。因此，在遠期市場上的交易者需要有良好的信譽。

不過，芝加哥商品交易所（國際貨幣市場）與倫敦國際金融期貨交易所等都建立了正式的外匯期貨市場。這些外匯期貨合約的面值都是標準化的，而且逐日盯市。更重要的是這些市場都有標準的結算程序，使得交易商很容易建立或沖銷頭寸。交易所的清算所要求交易者繳納足夠的保證金以保證合約能夠得到良好的履行，所以在交易中不需關注交易者的身份和信譽。

圖23-1是《華爾街日報》上外匯即期與遠期匯率行情表，表中給出的是1單位其他貨幣所兌換的美元數和1美元所兌換的其他貨幣的數額。圖23-2是期貨行情表，表中給出的是購買1單位外幣所需要的美元數額。圖23-1還同時給出了外匯的即期匯率和不同交割日的遠期匯率。

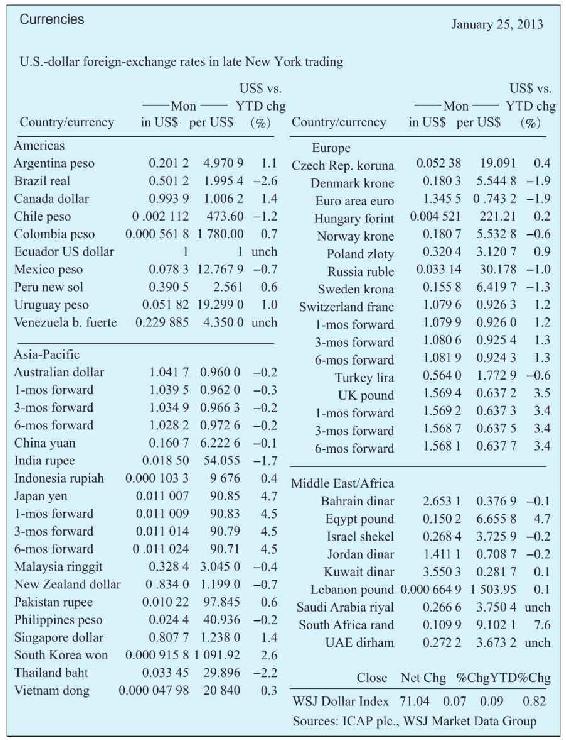
圖23-1　即期匯率與遠期匯率

圖23-1中所列的遠期匯率通常都採用每30天、90天或180天的滾動交割方式。這樣明天的遠期報價的到期日比今天報價的到期日晚一天。相比，圖23-2中的期貨合約都是在每年3月、6月、9月和12月的四個特定的到期日進行交割。

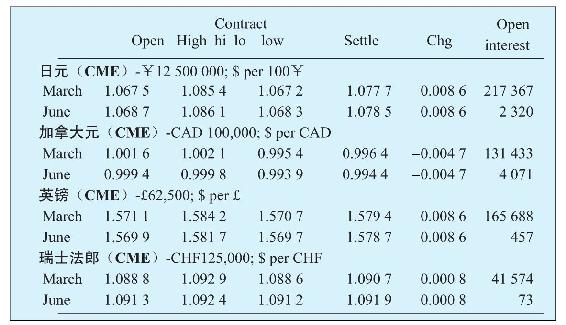
圖23-2　外匯期貨

23.1.2　利率平價

如同股票和股票期貨一樣，在完善的外匯市場上存在即期匯率與期貨價格之間的平價關係。如果這種所謂的利率平價關係（interest rate parity relationship）被違背，套利者就能夠在市場上以零淨投資獲得無風險利潤。他們的行為能使即期匯率和期貨價格回到平價關係上。利率平價關係也被稱為拋補利息套利關係（covered interest arbitrage relationship）。

我們可以用兩種貨幣——美元與英鎊來說明這種利率平價關係。設E₀為當前兩種貨幣的匯率，也就是說，買1英鎊需要E₀美元。F₀為遠期價格，即今天達成協議於今後某一時間T購買1英鎊所需的美元數目。設美國和英國兩國的無風險利率分別為r_US和r_UK。

根據利率平價理論，E₀與F₀之間的合理關係應該為

例如，如果每年的r_US=0.04，r_UK=0.05，而E₀=2美元/英鎊，那麼1年期遠期合約的理論期貨價格應該為

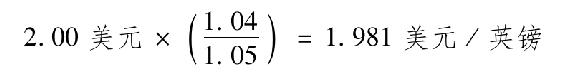
體會一下這個結果的含義，如果r_US小於r_UK，即把資金投在美國比投在英國增值慢，那麼為什麼不是所有的投資者都決定把他們的資金投在英國呢？一個重要的原因就是美元相對於英鎊會升值，所以儘管在美國的美元投資比在英國的英鎊投資增值慢，但是隨著時間的推移，每美元能換得的英鎊數目會越來越多，這正好抵消了英國的高利率所帶來的好處。

只要確定式（23-1）中美元升值是怎樣表現出來的，我們就可以得到這個結論。如果美元升值，即購買1英鎊所需要的美元數目越來越少，那麼遠期匯率F₀（等於1年以後交割時購買1英鎊所需要的美元數量）一定小於即期匯率E₀。這正是式（23-1）告訴我們的：當r_US小於r_UK時，F₀肯定小於E₀。由F₀比E₀得到的美元升值程度恰好可以與兩國利率之間的差額相抵消。當然，如果情況相反，結論正好顛倒過來：當r_US大於r_UK時，F₀肯定大於E₀。

【例23-1】拋補利息套利

如果利率平價被違背會怎麼樣呢？例如，假定期貨價格是1.97美元/英鎊而不是1.981美元/英鎊，那麼採取以下策略。用E₁表示1年後的匯率（美元/英鎊），當然它應該是一個隨投機者現在的期望而改變的隨機變量。

第一步，你把從英國借入的1英鎊按即期匯率兌換成2美元，1年以後你必須還本付息。因為貸款是在英國按英國利率借入的，所以你需要償還1.05英鎊，而它相當於E₁（1.05）美元。第二步，在美國的貸款是按美國利率的4%借出的。第三步是期貨頭寸，你先按1.97美元/英鎊的價格買入1.05英鎊，然後以匯率E₁把它換成美元。

在這裡，匯率風險正好被第一步的英鎊借款與第三步的期貨頭寸抵消了，所以按此策略所獲得的利潤是無風險的，並且不需要任何淨投資。

將例23-1中的策略推而廣之：

讓我們再回顧一下該套利過程。第一步是在英國借入1英鎊，然後將這1英鎊按即期匯率E₀兌換成E₀美元，這是現金流入。1年後，這筆英鎊貸款要還付本息，共需支付（1+r_UK）英鎊，或E₁（1+r_UK）美元。第二步，把由英鎊貸款換得的美元投在美國，這包括一個E₀美元的現金流出和一個1年後美元的現金流入E₀（1+r_US）。最後，英鎊借款的匯率風險由第三步的套期保值來消除，即事先通過期貨合約中買入（1+r_UK）英鎊以償還英國的貸款。

套利的淨利潤是無風險的，它等於E₀（1+r_US）-F₀（1+r_UK）。如果這個值是正的，就在英國借款，在美國貸款，然後建立期貨多頭頭寸以消除匯率風險。如果這個值是負的，就在美國借款，在英國貸款，然後建立英鎊期貨的空頭頭寸。當價格正好相符排除了套利機會時，這個表達式一定為零。把這個表達式整理可得

這就是1年期的利率平價關係（也稱為拋補利率平價）。

【例23-2】拋補利息套利

大量的經驗數據都證實了利率平價關係。例如，2013年2月3日，6個月到期以美元計價的LIBOR是0.48%，而英鎊的利率是0.65%。因此，我們期望遠期匯率低於即期匯率。正如我們所觀察到的：即期匯率是1.5694美元/英鎊，遠期匯率是1.5681美元/英鎊。更確切地來說，根據利率平價關係得到的遠期匯率是：1.5694×（1.0048/1.0065）^1/2=1.5681美元/英鎊，與實際利率相等。

概念檢查23-1

如果初始期貨價格F₀=2.01美元/英鎊，例23-1中如何設計套利策略？可以獲得的利潤是多少？

23.1.3　直接與間接報價

例23-1和例23-2中的匯率是以每英鎊多少美元的形式表示的，這是一種直接匯率報價方式，歐元-美元也是直接報價的一種典型方式。相反，很多匯率的報價都是每美元多少外幣（日元、瑞士法郎）的間接報價方式，比如92日元/美元。美元貶值反映在報價中就是匯率的下跌（1美元可以買到的日元比原來更少了）；相反，美元對英鎊貶值後匯率升高（需要更多的美元來購買1英鎊）。如果匯率是以每美元多少外幣表示，那麼式（23-2）中的國內和國外的匯率必須交換一下，這種情況下公式變為

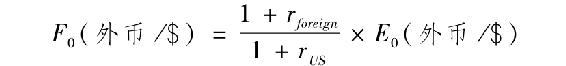
如果美國的利率高於日本，那麼美元在遠期市場的售價就會比即期市場的低（能夠購買的日元數量減少）。

23.1.4　利用期貨管理匯率風險

假定有一家美國公司，其產品的大部分都出口英國。公司就很容易受到美元/英鎊匯率波動的影響。首先，從客戶處得來的英鎊的美元價值隨匯率波動而波動；其次，公司在英國對客戶收費的英鎊價格也會受到匯率的影響。例如，如果英鎊相對於美元貶值了10%，那麼為了維持與過去同樣的美元等值的價格，該公司必須提高10%的英鎊價格。但是，如果該公司面臨英國產品製造商的競爭，卻未必能提升10%的價格，或者它認為提高英鎊價格會降低對其產品的需求。

為了抵消這種外匯變動的風險，公司可能從事一些在英鎊貶值時能帶來利潤的交易。這樣貶值導致的業務上的虧損能夠被金融交易上的利潤所抵消。例如，該公司買入一張期貨合約以今天協定的匯率把英鎊兌換成美元。如果英鎊貶值，那麼期貨頭寸就會產生利潤。

例如，假定3個月交割的英鎊期貨價格是2.00美元/英鎊，如果該公司持有一張價格為2美元/英鎊的期貨合約，3個月後匯率變為1.90美元/英鎊，那麼英鎊空頭頭寸的利潤是F₀-F_T=2.00美元-1.90美元=0.10美元。

為了儘量抵消匯率波動帶來的風險，需要在期貨市場上賣出多少英鎊合適呢？假如英鎊每貶值0.10美元，下一個季度利潤的美元價值就會下滑200000美元，那麼進行套期保值時，英鎊每貶值0.10美元，期貨頭寸需要帶來的利潤為200000美元，因此我們需要的期貨頭寸是2000000英鎊。正如我們剛才看到的，期貨合約每英鎊的利潤等於當前期貨價格與最終匯率之差，因此0.10美元的貶值^[1]所帶來的外匯利潤=0.10美元×2000000=200000美元。

只要利潤與匯率之間的關係大致是線性的，英鎊期貨的正確套利頭寸就與英鎊的實際貶值無關。例如，如果英鎊只是貶值了上述的一半，即0.05美元，公司的經營利潤就只會損失100000美元。期貨頭寸也只會得到上述利潤的一半，即0.05美元×2000000=100000美元，同樣恰好抵消了經營的風險。如果英鎊升值了，套期保值仍然會抵消經營的風險，只是這種情景不見得是好事。如果英鎊升值了0.05美元，公司可能會由於英鎊升值而獲得100000美元的收益；然而，由於公司有義務按照初始的期貨價格交割英鎊，公司就會有等量的損失。

對衝比率就是用來給未受保護的資產組合套期保值所必需的期貨頭寸數目，在這個例子中資產組合是指公司的出口業務。通常，我們可以把對衝比率當成為了抵消某一特定未受保護頭寸的風險而建立的套期保值工具的數量（比如，期貨合約）。在這個例子中，對衝比率H就是

因為芝加哥商品交易所中每張期貨合約需要交割62500英鎊，那麼你就需要賣出2000000/62500=32張合約。

概念檢查23-2

假定美元貶值時，一家跨國公司受到了損失。具體地，假定英鎊兌美元每上升0.05美元，該公司利潤就會減少200000美元，那麼該公司需要持有多少張合約？應該持有多頭還是空頭合約？

對於對衝比率的一種解釋是作為不確定性的基本來源敏感度的一種比率。匯率每波動0.10美元，經營利潤的敏感度是200000美元。匯率每波動0.10美元，期貨利潤的敏感度是待交割的0.10美元/英鎊。因此，對衝比率是200000/0.10=2000000（英鎊）。

對衝比率同樣可以根據期貨合約來定義。因為每張合約需要交割62500英鎊，則匯率每波動0.10美元給每張合約帶來的利潤是6250美元。因此，以期貨合約為單位的對衝比率就是200000美元/6250美元=32張合約，正如上面所得到的。

給定了未進行套期保值頭寸對匯率變化的敏感度後，計算風險最小化的套期保值頭寸就容易多了。但是敏感度的估計是比較困難的。例如，對於出口公司來說，一種比較幼稚的觀點就是我們只需要估計預期的英鎊計價的收入，然後在期貨市場或遠期市場交割該數目的英鎊合約。然而，這種方法未能認識到英鎊收入本身就是匯率的一個函數，因為該美國公司的競爭地位部分是由匯率決定的。

另一種方法則部分依賴於歷史關係。例如，假定該公司準備了圖23-3所示的一張散點圖，該圖把公司最近40個季度以來每個季度以美元計價的經營利潤與該季度美元兌英鎊的匯率聯繫起來。匯率較低，也就是英鎊貶值時，利潤一般來說比較低。為了對敏感度定量化，我們可以估計迴歸方程

利潤=a+b（美元/英鎊匯率）

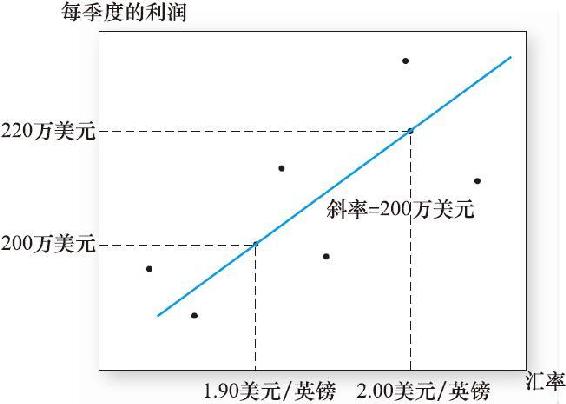
圖23-3　利潤是匯率的函數

迴歸得到的斜率，也就是b的估計值，就是季度利潤對匯率的敏感度。例如，如果b的估計值是2000000，如圖23-3所示，那麼平均來說，英鎊兌美元每增加1美元就會帶來2000000美元的利潤增量。這當然是我們在斷定英鎊兌美元的匯率下跌0.1美元會使利潤減少200000美元假定的敏感度。

當然，解釋這些迴歸結果必須小心。例如，我們不能把一段時間內匯率在每英鎊1.80~2.10美元波動時的利潤和匯率的歷史關係外推至匯率低於1.40美元/英鎊或者高於2.50美元/英鎊的情形。

概念檢查23-3

聯合米勒公司購買玉米做玉米片。玉米價格上漲時，穀類食品製造成本上升，從而利潤降低。從歷史上來看，每一季度的利潤與玉米價格的關係都滿足方程：利潤=800萬美元-100萬×價格/蒲式耳。為了對玉米價格風險進行套期保值，聯合米勒公司應該在玉米期貨市場購買多少蒲式耳玉米？

另外，把過去的關係外推至將來時也必須小心。在第8章中，我們就已經看到指數模型迴歸的貝塔傾向於隨時間的變化而變化；這樣的問題不僅僅出現在指數模型中。更進一步地說，迴歸估計僅僅是一個估計。有些時候一個迴歸方程的參數也可能相當不精確。

對尋找一個變量對另外一個變量的平均敏感度來說，歷史關係通常是一個很好的出發點。這些斜率係數不是完美的，但仍然是有用的對衝比率的指標。

[1] 實際上，合約的利潤取決於期貨價格的變化，而不是即期匯率。為簡單起見，我們把期貨價格的下跌稱為英鎊的貶值。