BUSINESS BOOKS

CFA考題

1.Abco公司董事會正在擔心公司養老金計劃中1億美元股票資產組合的下跌風險。該董事會的顧問提議暫時（一個月）用期貨或者期權對衝這個資產組合。該顧問引用了下表，並陳述道：

a.“通過賣出（做空）4000個期貨合約，這個1億美元股票資產組合能夠完全規避下跌風險”。

b.“這種保護方法的成本就是該資產組合的期望收益率為0”。

市場、資產組合與合約數據

請評價該顧問每一個陳述的精確性。

2.特許金融分析師邁克爾·韋伯正在對期權定價的一些方面進行分析，包括期權價值的決定因素，不同期權定價模型的特性，以及計算所得的期權價值與期權市場價格可能存在的背離。

a.如果標的股票波動率降低，對股票看漲期權價值的預期影響是什麼？如果期權的到期期限增加呢？

b.使用布萊克-斯科爾斯定價模型，韋伯計算了3個月看漲期權的價值並注意到該計算值與期權市場價格不同。關於韋伯對布萊克-斯科爾斯期權定價模型的應用：

i.討論為什麼處於虛值的歐式期權的計算價值可能與它的市場價格不同。

ii.討論為什麼美式期權的計算價值可能與它的市場價格不同。

3.富蘭克林是一位負責衍生證券的資產組合管理人。富蘭克林觀察到具有同樣行權價格、到期期限和標的股票的美式期權與歐式期權。富蘭克林認為歐式期權比美式期權具有更高的權利金。

a.試評論富蘭克林認為該歐式期權會有較高權利金的觀點。富蘭克林被要求對Abaco有限公司股票的1年期歐式看漲期權定價，該股票最後交易價格為43.00美元。他已經蒐集瞭如下信息：

b.使用看跌-看漲期權平價和以上信息計算歐式看漲期權的價值。

c.試說明以下三個變量對看漲期權價值的影響（無須計算）。

i.短期利率提高

ii.股票價格波動率上升

iii.期權到期期限縮短

4.現在某股票指數在50點水平交易。特許金融分析師保羅·瑞普想運用二項式模型對2年期的指數期權估價。股票指數可能上升20%或者下降20%，年無風險利率為6%，指數中的任何成分股都不派發股利。

a.構造一個用於股票指數定價的兩期二叉樹。

b.計算行權價格為60點的該指數歐式看漲期權的價值。

c.計算行權價格為60點的該指數歐式看跌期權的價值。

d.證明你計算的看漲期權與看跌期權的價值滿足看跌-看漲期權平價。

5.肯·韋伯斯特管理著以標準普爾500指數為基準的2億美元的股票資產組合。韋伯斯特認為若用一些傳統的基礎經濟指標來測量的話，市場被高估了。他擔心潛在的損失，但是認識到標準普爾500指數仍可能超過目前1136的水平。

韋伯斯特正在考慮以下的雙限期權策略。

·購買一份行權價格為1130（剛剛處於虛值狀態）的標準普爾500指數看跌期權，使資產組合受到保護。

·賣掉兩份行權價格為1150（處於深度虛值狀態）的看漲期權，來獲取買入一份看跌期權所需的資金。

·因為兩份看漲期權的綜合德爾塔（見下表）小於1（即2×0.36=0.72），如果市場繼續發展，這些期權的損失也不會超過標的資產組合的盈利。

下表就是用於構造雙限期權的信息：

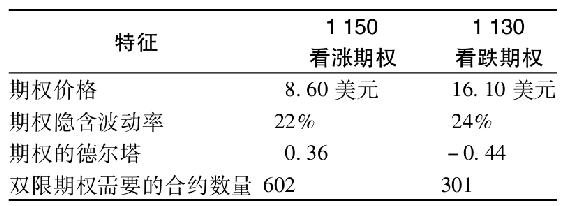
注：1.忽略交易成本。

2.標準普爾500指數30天曆史波動率=23%。

3.期權到期期限=30天。

a.如果30天后標準普爾500指數發生瞭如下變化，請描述這些綜合資產組合（標的資產組合加雙限期權）的潛在收益：

i.上升約5%至1193點。

ii.保持在1136點（無變化）。

iii.下降約5%至1080點。

（無須計算。）

b.對於標準普爾500指數達到了a中所列的每一種情況，討論這些情況對每個期權對衝比率（德爾塔）的影響。

c.根據提供的波動率數據，評估以下每個期權的定價：

i.看跌期權

ii.看漲期權