e1 Zvi Bodie 投資學 v10
習題
基礎題
1.本章中,我們表明看漲期權價值隨股票波動率增加而增加。這對看跌期權價值也正確嗎?利用看跌-看漲期權平價定理和數字例子來證明你的答案。
2.你認為看漲期權行權價格增加1美元會導致看漲期權價值減少量大於還是小於1美元?
3.高貝塔股票看跌期權的價值是否高於低貝塔股票看跌期權的價值?股票具有相同的公司特定風險。
4.其他條件都相同,公司特定風險較大的股票看漲期權的價值是否高於公司特定風險較小的股票看漲期權的價值?兩種股票的貝塔值相同。
5.其他條件都相同,較高行權價格的看漲期權與較低行權價格的看漲期權相比,對衝比率高還是低?
中級題
6.在下列各題中,你被要求比較給定參數的兩種期權。假定無風險利率為6%,期權標的股票不支付股利。
a.
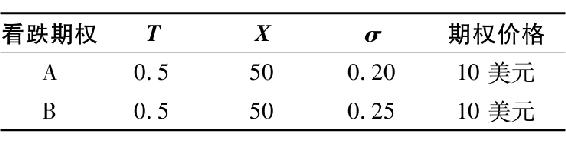
股票價格較低時,賣出哪一種看跌期權?
i.A
ii.B
iii.信息不足
b.
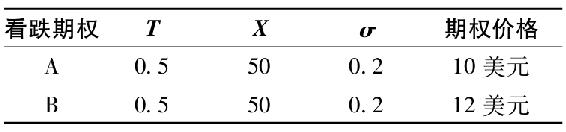
股票價格較低時,一定賣出哪一種看跌期權?
i.A
ii.B
iii.信息不足
c.

哪一種看漲期權的期限較短?
i.A
ii.B
iii.信息不足
d.

股票波動率較高時,賣出哪一種看漲期權?
i.A
ii.B
iii.信息不足
e.

股票波動率較高時,賣出哪一種看漲期權?
i.A
ii.B
iii.信息不足
7.重新考慮兩狀態模型中對衝比率的確定過程,我們證明了1/3股股票就能對衝1份期權。當行權價格分別為120、110、100、90時,對衝比率各是多少?隨著期權實值程度的逐漸提高,對衝比率會如何變化?
8.證明布萊克-斯科爾斯看漲期權對衝比率隨股票價格上升而上升。考慮行權價格為50美元的1年期期權,其標的股票的年標準差為20%。短期國債收益率為每年3%。股票價格分別為45美元、50美元和55美元時,求N(d1)。
9.在本題中,我們將推導兩狀態看跌期權的價值。數據:S0=100,X=110,1+r=1.10。ST兩種可能的價格為130和180。
a.證明兩狀態間S的變動範圍是50,而P的變動範圍是30。看跌期權的對衝比率是多少?
b.構建一個資產組合,包括3股股票和5份看跌期權。該資產組合的收益(非隨機)是多少?該資產組合的現值是多少?
c.給定股票現在售價為100,求解看跌期權的價值。
10.計算第9題中行權價格為110的股票看漲期權的價值。證明你對第9題和第10題的答案滿足看跌-看漲期權平價定理。(在此例中不要使用連續複利計算X的現值,因為這裡我們使用的是兩狀態模型,不是連續時間的布萊克-斯科爾斯模型。)
11.根據以下信息,使用布萊克-斯科爾斯公式計算股票看漲期權的價值。

12.與第11題中看漲期權的行權價格和到期期限相同,使用布萊克-斯科爾斯公式計算股票看跌期權的價值。
13.重新計算第11題中的看漲期權價值。保持其他變量不變,以下列條件逐一替代第11題中的原有條件:
a.到期期限=3個月
b.標準差=25%每年
c.行權價格=55美元
d.股票價格=55美元
e.利率=5%
獨立考慮每一種情形。證明期權價值的變化與表21-1中的預測保持一致。
14.看漲期權X=50美元,標的股票價格S=55美元,看漲期權售價為10美元。根據波動率估計值σ=0.30,你會發現N(d1)=0.6,N(d2)=0.5,無風險利率為0。期權價格的隱含波動率高於還是低於0.30?為什麼?
15.在表21-3中,跨式期權頭寸布萊克-斯科爾斯價值的Excel公式是什麼?
閱讀以下案例,回答第16~21題。特許金融分析師馬克·華盛頓是BIC的分析師。一年前,BIC分析師預測美國股票市場將輕微下降並建議對BIC的資產組合進行德爾塔對衝。正如預測,美國股票市場在12個月確實下跌了近4%。但是,BIC資產組合的表現令人失望,低於同行表現近10%。華盛頓被指派去檢查期權策略,以確定對衝資產組合的表現不如預期的原因。
16.哪一個是德爾塔中性資產組合的最佳表述?德爾塔中性資產組合完全對衝了:
a.標的資產價格的小幅變化。
b.標的資產價格的小幅下跌。
c.標的資產價格的任何變化。
17.在討論了德爾塔中性資產組合的概念之後,華盛頓決定有必要進一步解釋德爾塔的概念。華盛頓畫出了把期權價值當作標的股票價格的函數。該圖形表明了德爾塔該如何解釋。德爾塔是:
a.期權價格圖形中的斜率。
b.期權價格圖形中的曲率。
c.期權價格圖形中的水平線。
18.華盛頓考慮了一個德爾塔為-0.65的看跌期權。如果標的資產價格下跌了6美元,那麼期權價格的最佳估計是什麼?
19.BIC擁有51750股史密斯公司股票。每股售價為69美元。行權價格為70美元的史密斯公司股票看漲期權售價為3.50美元,其德爾塔為0.69。構建一個德爾塔中性對衝,需要多少份看漲期權?
20.回到第19題。如果股票價格下跌,德爾塔對衝需要賣出看漲期權的數量是增加還是減少?
21.對於德爾塔中性資產組合的目標,下列哪種陳述最精確?一個德爾塔中性資產組合是結合一個______。
a.股票多頭和看漲期權空頭,這樣股票價值變化時資產組合價值保持不變
b.股票多頭和看漲期權空頭,這樣股票價值變化時資產組合價值也發生變化
c.股票多頭和看漲期權多頭,這樣股票價值變化時資產組合價值保持不變
22.長期國債收益率對利率變動的敏感性是高於還是低於標的債券收益率對利率的敏感性?
23.如果股票價格下跌,看漲期權價格上升,那麼看漲期權的隱含波動率如何變化?
24.如果到期期限縮短,看跌期權價格上升,那麼看跌期權的隱含波動率如何變化?
25.根據布萊克-斯科爾斯公式,當股票價格趨於無限大時看漲期權對衝比率的值為多少?
26.根據布萊克-斯科爾斯公式,當行權價格很小時看跌期權對衝比率的值為多少?
27.IBM平值看漲期權的對衝比率為0.4,平值看跌期權的對衝比率為-0.6。IBM平值跨式期權頭寸的對衝比率為多少?
28.考慮一個6個月期限的歐式看漲期權,行權價格為105美元。標的股票售價為每股100美元,不支付股利。無風險利率為5%。如果期權現在售價為8美元,期權隱含波動率是多少?使用表21-3(可從www.mhhe.com/bkm下載,鏈接至第21章材料)回答這一問題。
a.進入電子數據中的工具菜單並選擇“Goal Seek”。對話框要求你回答三條信息。在那個對話框中,你通過改變單元格B2來設定E6單元格的值為8。換句話說,你讓電子表格尋求標準差的值(出現在單元格B2中),迫使期權的價值(單元格E6)等於8美元。然後點擊“OK”按鈕,你會發現看漲期權現在價值8美元,輸入的標準差隨之改變以保持與期權價值一致。這是期權價值為8美元時看漲期權隱含的標準差。
b.如果期權售價為9美元,隱含波動率如何變化?為什麼隱含波動率會增加?
c.如果期權價格保持在8美元,但是期權到期期限縮短(比如4個月),隱含波動率如何變化?為什麼?
d.如果期權價格保持在8美元,但是行權價格降低(比如100美元),隱含波動率如何變化?為什麼?
e.如果期權價格保持在8美元,但是股票價格下降(比如98美元),隱含波動率如何變化?
29.構建一個雙限期權:買入一股價格為50美元的股票,買入一份6個月期的行權價格為45美元看跌期權,並且賣出一份6個月期的行權價格為55美元的看漲期權。根據股票的波動率,你可以計算出6個月期、行權價格為45美元的期權,N(d1)=0.60,而行權價格為55美元的期權,N(d1)=0.35。
a.如果股票價格上升1美元,雙限期權盈利或損失是多少?
b.如果股票價格變得非常大,資產組合的德爾塔如何變化?如果股票價格變得非常小呢?
30.三份看跌期權的標的股票相同,德爾塔分別為-0.9、-0.5和-0.1。填表把德爾塔分配給相應的期權。
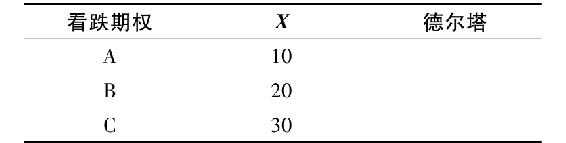
31.你非常強烈地看漲EFG股票,並認為其大大超過市場上其他股票。在下列每個問題中,如果你的看漲預測是正確的,選出給你帶來最大利潤的資產組合。說明你的理由。
a.選擇A:10000美元投資於看漲期權,X=50。
選擇B:10000美元投資於EFG股票。
b.選擇A:10份看漲期權合約(每份100股),X=50。
選擇B:1000股EFG股票。
32.你想持有XYZ公司股票的保護性看跌期權頭寸,鎖定年末最小价值為100美元。XYZ現在售價為100美元。下一年股票價格將上升10%或下降10%,短期國債利率為5%。不幸的是,沒有XYZ股票的看跌期權交易。
a.假定有所需要的看跌期權交易,購買它的成本是多少?
b.這一保護性看跌期權資產組合的成本是多少?
c.什麼樣的股票加國債頭寸將確保你的收益等於X=100的保護性看跌期權提供的收益?證明該資產組合的收益和成本與所需的保護性看跌期權相匹配。
33.回到例21-1。運用二項式模型對行權價格為110美元的1年期歐式看跌期權估價,該期權標的股票與原例中相同。你對看跌期權價格的計算結果是否滿足看跌-看漲期權平價?
34.假設無風險利率為0,美式看跌期權是否會被提前執行?解釋之。
35.用p(S,T,X)表示價格為S美元的股票歐式看跌期權的價值,到期期限為T,行權價格為X,並且用P(S,T,X)表示美式看跌期權的價值。
a.估算p(0,T,X)
b.估算P(0,T,X)
c.估算p(S,T,0)
d.估算P(S,T,0)
e.以b的答案說明美式看跌期權提前執行的可能性如何。
36.你嘗試對行權價格為100美元的1年期看漲期權進行估價。標的股票不支付股利,它現在售價為100美元,並且你認為有50%的機會上漲至120美元並有50%的機會下跌至80美元。無風險利率為10%。利用兩狀態股票價格模型計算看漲期權的價值。
37.考慮上題中股票波動率的增加。假定如果股票價格上升,就會增加至130美元;如果股票價格下跌,就會下跌至70美元。證明此時看漲期權價值大於第36題中計算的價值。
38.利用第36題中的數據,計算行權價格為100美元的看跌期權的價值。證明你的答案滿足看跌-看漲期權平價。
39.ZYZ公司將在2個月後支付每股2美元的股利。它的股票現在售價為每股60美元。XYZ公司股票看漲期權的行權價格為55美元,到期期限為3個月。無風險利率為每月0.5%,股票波動率(標準差)=7%每月。求偽美式期權的價值。(提示:試將一個月作為一“期”,而不是把一年作為一“期”。)
40.“通用電氣看漲期權的貝塔值高於通用電氣股票的貝塔值。”這一說法正確還是錯誤?
41.“行權價格為1330的標準普爾500指數看漲期權的貝塔值高於行權價格為1340的指數看漲期權的貝塔值。”這一說法正確還是錯誤?
42.當股票價格變得非常大時,可轉換債券的對衝比率如何變化?
43.高盛公司認為在今後的三年中市場波動率將為每年20%。市場指數的3年期平值看漲與看跌期權以隱含波動率為22%的價格出售。高盛公司應該建立什麼樣的資產組合對波動率進行投機,而不用建立市場牛市或熊市頭寸?使用高盛對波動率的估計值,3年期平價期權的N(d1)=0.6。
44.你持有股票的看漲期權。股票的貝塔為0.75,並且你擔心股票市場可能會下跌。股票現在售價為5美元,並且你持有100萬份股票期權(你持有10000份合約,每份100股股票)。期權的德爾塔為0.8。為了對衝你的市場風險敞口,你需要買入或賣出多少市場指數資產組合?
45.設想你是一位資產組合保險的提供商。你正在建立一個為期4年的項目。你管理的資產組合現在價值1億美元,並且你希望最小收益為0。股票資產組合的標準差為每年25%,短期國債利率為每年5%。簡單起見,假定資產組合不支付股利(或者所有股利可以再投資)。
a.多少錢用來購買國債?多少錢用來購買股票?
b.如果第一個交易日股票資產組合就下跌了3%,作為管理人你應該如何處置?
46.假定行權價格為90美元的3個月埃克森美孚股票看漲期權正在以隱含波動率為30%的價格出售。埃克森美孚股票現在價格為每股90美元,並且無風險利率為4%。如果你認為股票的真實波動率為32%,在不承擔埃克森美孚業績風險的情況下,以你的觀點,你該如何交易?對於賣出或買入的每一份期權合約,你需要持有多少股股票?
47.使用第46題中的數據,假定行權價格為90美元的3個月看跌期權以隱含波動率為34%的價格出售。構建一個包含看漲期權與看跌期權頭寸的德爾塔中性資產組合,當期權價格恢復到調整後的正確價格時該資產組合能獲得利潤。
48.假定摩根大通出售價值為125萬美元、貝塔值為1.5的股票資產組合的看漲期權。期權德爾塔為0.8。摩根大通想通過買入市場指數資產組合來對衝市場變化的風險。
a.摩根大通需要購買價值多少美元的市場指數資產組合來對衝它的頭寸?
b.如果摩根大通使用市場指數看跌期權來對衝風險,該怎麼辦?買入還是賣出看跌期權?每份看跌期權對應100單位的指數,並且當前的指數價格代表價值1000美元的股票。
49.假如你正在計算一隻尚有一年到期的股票期權的價值,隱含浮動利率(年標準差)為σ=0.4,如果你的二項式模型是用以下數據建立的,那麼u和d的值是多少
a.一年的時間
b.4個時間段,每段時間為3個月
c.12個時間段,每段時間為1個月
50.你建立了一個二項式模型,為一個週期,並斷言在一年的過程中,股票價格將上升1.5或下降2/3,你對明年股票回報率波動性的隱含假設是什麼?
51.利用期權平價關係證明,一個無息股票的平價看漲期權的成本高於平價看跌期權。若S=(1+r)T看跌與看漲期權的價格相當。
52.返回到問題36,使用華爾街實戰21-1中所描述的“風險中性”,來評估看漲期權的價值。確認你的答案與你所使用的兩種方法的值相匹配。
53.返回到問題38,如果股票漲了,你的收益是多少?如果股票價格下跌,會有什麼回報呢?使用華爾街實戰21-1中圖表所描述的“風險中性”,來評估看漲期權的價值。確認你的答案與你所使用的兩個方法的值相匹配。