e1 Zvi Bodie 投資學 v10
21.6 期權定價的經驗證據
布萊克-斯科爾斯期權定價模型已經經受了無數次的實證檢驗。在絕大多數情況下,研究結果表明通過該公式計算的期權價格與實際價格相當接近。與此同時,該模型也不時呈現一些缺陷。
最大的問題是波動性,如果模型是準確的,所有到期日相同的股票期權的隱含波動性都應當相等——畢竟,每隻股權的到期日和基礎資產是相同的,由此產生的隱含波動性也應是相同的。但事實上,當把隱含波動率看成行權價格的一個函數時,典型的結果如圖21-15所示,它將標準普爾500指數期權作為標的資產。隱含波動率穩步下降,行權價格上漲。顯然,布萊克-斯科爾斯模型缺少了一些東西。
魯賓斯坦[1]認為模型的問題與類似於1987年10月市場崩盤的恐懼有關。如果股票價格變化平緩,深度虛值的看跌期權幾乎毫無價值,因為在短時間內股票價格大幅下跌(看跌期權變為實值)的概率很小。但是一個突然的價格暴跌會使看跌期權變為實值,就像市場崩盤,從而給予期權更高的價值。這樣,股票價格大幅下跌的可能性很大,市場對這些期權的定價會比布萊克-斯科爾斯公式的定價更高。高期權價格的結果會是由布萊克-斯科爾斯模型推導出更高隱含波動率。
有趣的是,魯賓斯坦指出1987年股市崩盤之前,像圖21-15中的隱含波動率的軌跡相對平坦,與那時市場不擔心股市崩盤的觀念相一致。但是,股市崩盤後隱含波動率的軌跡就開始向下傾斜,呈現出所謂的“期權微笑”形狀。當我們使用允許更一般股票價格分佈(包括崩盤風險和波動率隨機變化)的期權定價模型時,它們產生類似於圖21-15中向下傾斜的隱含波動率曲線。[2]
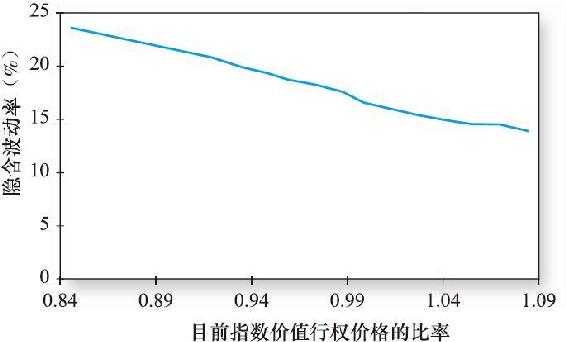
圖21-15 把標準普爾500指數隱含波動率當作行權價格的函數
資料來源:Mark Rubinstein,“Implied Binomial Trees,”Journal of Finance(July 1994),pp.771-818.
[1] Mark Rubinstein,“Implied Binomial Trees,”Journal of Finance 49(July 1994),pp.771-818.
[2] 這些更一般模型的拓展分析,參見:R.L.McDonald,Derivatives Markets,3rd ed.(Boston:Pearson Education[Addison-Wesley],2006).