e1 Zvi Bodie 投資學 v10: 21.4 布萊克-斯科爾斯期權定價

e1 Zvi Bodie 投資學 v10

21.4　布萊克-斯科爾斯期權定價

儘管二項式模型非常靈活，但這種方法在實際交易中需要用計算機。期權定價公式要更為簡單，沒有二項式模型中複雜的算法。只要做兩個假設，公式就可以使用，這兩個假設是無風險利率與股票價格的波動率在期權有效期內保持不變。在這種情況下，到期日前的時間被細分成更多的間隔，到期日股票價格分佈漸近於對數正態分佈，如圖21-5所示。當股票價格分佈是真正的對數分佈時，我們可以得出精確的期權定價公式。

21.4.1　布萊克-斯科爾斯公式

在布萊克、斯科爾斯^[1]與默頓^[2]得出看漲期權定價公式之前，金融經濟學家們一直在尋求一種實用的期權定價模型。斯科爾斯與默頓因此獲得了1997年諾貝爾經濟學獎。^[3]現在，布萊克-斯科爾斯定價公式（Black-Scholes pricing formula）已被期權市場參與者廣泛使用。看漲期權的定價公式為

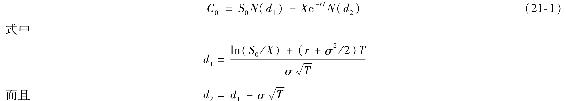
而且d₂=d₁-σ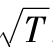

C₀——當前的看漲期權價值；

S₀——當前的股票價格；

N（d）——標準正態分佈小於d的概率，圖21-6中的陰影部分，在Excel中，這個函數叫NORMSDIST（）；

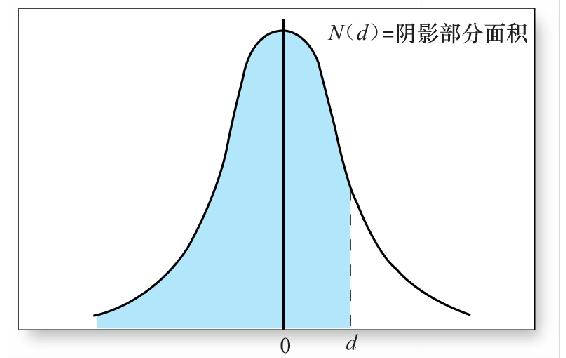
圖21-6　標準正態曲線

X——行權價格；

e——自然對數的底，約為2.71828。在Excel中，可以使用EXP（x）函數計算e^x；

r——無風險利率（與期權到期期限相同的安全資產連續複利的年收益率，與離散時間的收益率r_f不同）；

T——期權到期時間，按年記；

ln——自然對數函數，在Excel中，可以用LN（x）函數計算ln（x）；

σ——股票連續複利的年收益率的標準差。

注意，式（21-1）有一個驚奇的特點：期權價值並不取決於股票的期望收益率。在某種意義上說，含有股票價格的定價公式已經包括了該信息，因為股票價格取決於股票的風險與報酬特徵。這裡的布萊克-斯科爾斯公式假定股票不支付股利。

儘管你會覺得布萊克-斯科爾斯公式令人生畏，但是我們可以從直覺上理解。技巧是把N（d）項（不嚴謹地）視為看漲期權在到期處於實值的風險調整概率。首先，看一下式（21-1），假定兩個N（d）項都接近於1.0，也就是說，看漲期權被執行的概率很高。於是看漲期權價值等於（S₀-Xe^-rT），這也是我們前面提到過的調整後內在價值［S₀-PV（X）］。這一點很有意義，如果確實執行了，我們就獲得了現在價格為S₀的股票的索取權，而承擔了現值PV（X）的義務，或者以連續複利計算的義務Xe^-rT。

現在再看式（21-1），假定N（d）項接近於0，意味著期權不會被執行。於是該等式說明看漲期權毫無價值。對於N（d）項，取值範圍為0~1時，式（21-1）告訴我們可以把期權價值視為看漲期權潛在收益的現值，該收益經過到期時處於實值的概率調整。

N（d）項又是如何表示風險調整概率呢？這需要用到高級統計學的知識。注意，ln（S₀/N）在d₁和d₂的分子中都出現了，它近似表示現在期權處於實值和虛值的百分比。例如，如果S₀=105，X=100，期權處於實值的百分比為5%，即ln（105/100）=0.049。同理，如果S₀=95，期權處於虛值的百分比為5%，即ln（95/100）=-0.051。分母σ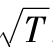，用股票價格在剩餘期限中標準差對期權的實值與虛值的百分比進行調整。當股票價格變動很小，並且距到期時間也所剩無幾的時候，給定比例的實值期權一般會保持實值狀態。因此，N（d₁）和N（d₂）表示期權到期時處於實值的概率。

【例21-4】布萊克-斯科爾斯定價

你可以很容易地使用布萊克-斯科爾斯公式。假定你想對一個看漲期權進行定價，已知條件如下：

首先計算：

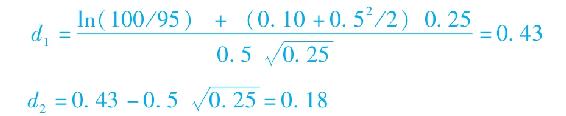
接下來查N（d₁）和N（d₂）。在很多統計學課本里可以查到正態分佈表（見表21-2）。任何電子數據表程序也提供正態分佈函數N（d）。例如，在Excel中，程序名稱為NORMSDIST。利用Excel或表21-2，我們可得到：

N（0.43）=0.6664

N（0.18）=0.5714

於是，看漲期權的價值為：

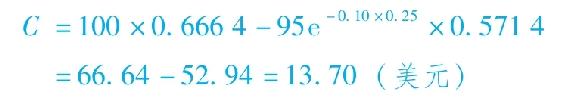
概念檢查21-6

若標準差不是0.5而是0.6，重新計算例21-4中看漲期權的價值。確認股票報酬波動率越大，期權價值越大。

表21-2　累積正態分佈

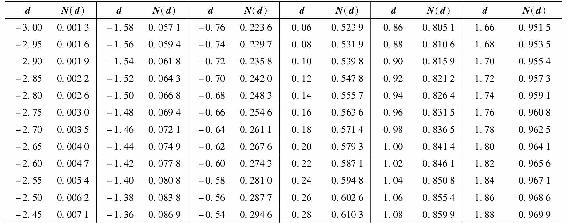
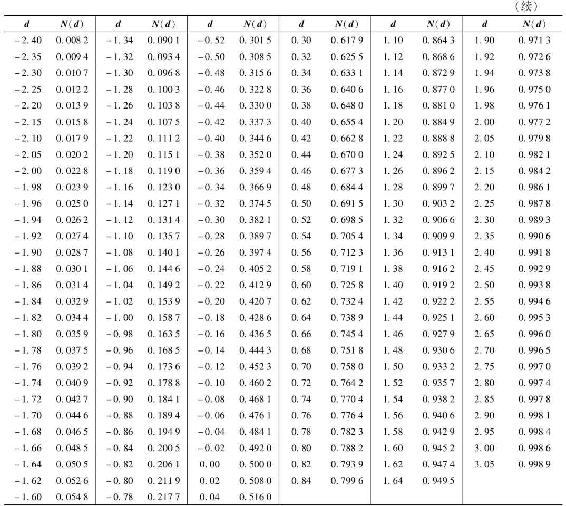
如果例21-2中期權價格是15美元而不是13.70美元，那又會怎麼樣呢？是不是期權被錯誤定價了？也許是，但在賭運氣之前，應再考慮估價分析。首先，同所有模型一樣，布萊克-斯科爾斯公式也是建立在使該模型近似有效的抽象簡化基礎之上的。

公式的一些重要假設如下：

·在期權到期日之前，股票不支付股利。

·利率r與股票的方差σ²保持不變（或者更一般化地，兩者都是時間的已知函數，任何變化都可預測）。

·股票價格是連續的，也就是說股票價格不會發生異常的波動，比如公司被接管聲明導致的價格異常波動。

如令已有變形的布萊克-斯科爾斯公式來處理以上的這些限制條件。

其次，在布萊克-斯科爾斯模型中，你必須保證公式中各個參數都是正確的。其中的四個值（S₀、X、T和r）都是很直接的。股票價格、行權價格和到期期限都是給定的。利率是相同期限的貨幣市場利率，並且股利支付至少在短期內是可以合理預測的。

最後一個輸入變量是股票收益率的方差，不能直接觀察到。必須從歷史數據、情境分析或者其他期權價格中估計出來，我們接下來討論這個問題。

我們在第5章講過，股票市場收益率的歷史方差可以從n個觀察值得到，其公式如下：

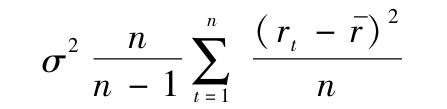
其中，r為樣本期的平均收益率。在t天的收益率被定義為r_t=ln（S_t/S_t-1），與連續複利一致。［注意，一個比率取自然對數，其值近似等於分子與分母的百分比差異，於是ln（S_t/S_t-1）可以用來測度t-1期至t期的股票收益率。］歷史方差一般用幾個月的每日收益來計算。因為股票波動率是估計出來的，所以真實的期權價格與用公式算出的期權價格有可能不同，這是由股票的波動率估計誤差造成的。

事實上，市場參與者往往從不同的角度來看期權定價問題。他們不是用所給的股票標準差按布萊克-斯科爾斯公式計算期權價格，而是會問：如果我觀察到的期權價格與布萊克-斯科爾斯公式計算出來的期權價格一致的話，那麼標準差是多少呢？這就是期權的隱含波動率（implied volatility），即期權價格中隱含的股票波動率水平。^[4]投資者可以判斷實際的股票標準差是否超過了隱含波動率。如果超過了，則購買期權是一個好的選擇；如果實際波動率高於隱含波動率，期權的公允價格就會高於觀察到的價格。

另一個角度是比較到期日相同、行權價格不同的同一股票的期權。具有較高隱含波動率的期權相對貴一些，因為需要較高的標準差來調節價格。分析師認為應該買入低隱含波動率期權，賣出高隱含波動率期權。

布萊克-斯科爾斯定價公式，以及隱含波動率，很容易使用Excel中的電子數據表計算，如表21-3所示。模型的輸入部分在B列，輸出部分在E列。表格中還給出了d₁和d₂的計算公式，Excel中的公式NORMSDIST（d₁）用來計算N（d₁）。單元格E6中有布萊克-斯科爾斯公式。（表21-3中實際上包含了對股利的調整，下一節將對此進行描述。）

表21-3　利用布萊克-斯科爾斯公式計算期權價值

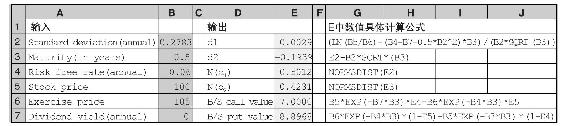
如需計算隱含波動率，我們可以使用Excel工具菜單中的目標搜索（Goal Seek）命令，如圖21-7所示。目標搜索命令可以讓我們通過改變一個單元格的值以使另一個單元格（稱為目標單元格）的值等於一個特定的值。例如，如果我們看到一個售價為7美元的看漲期權，其他輸入部分如表格所示，則我們可以利用目標搜索命令改變B2單元格的值（股票的標準差），從而可以使E6單元格的值等於7美元。目標單元格E6就是看漲期權的價格，電子數據表會計算出單元格B2的相應值。當你點擊“OK”按鈕時，電子數據表就會發現標準差0.2783與看漲期權價格7美元相符；如果期權售價是7美元，則該標準差就是期權的隱含波動率。

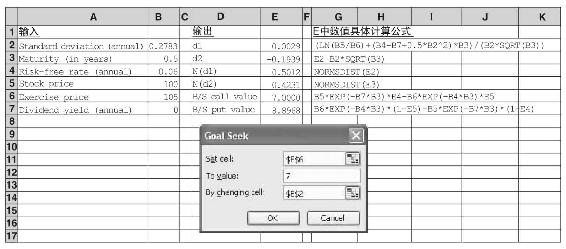
圖21-7　利用目標搜索確定隱含波動率

芝加哥期權交易所定期計算主要股票指數的隱含波動率。圖21-8是1990年以來標準普爾指數30天隱含波動率走勢。在動盪時期，隱含波動率會迅速突起。注意1991年1月（海灣戰爭）、1998年8月（長期資本管理公司破產）、2001年9月11日、2002年（入侵伊拉克）和2008年次貸危機的波動率高峰。因為隱含波動率與危機相關，所以它有時被稱為“投資者恐懼指數”。

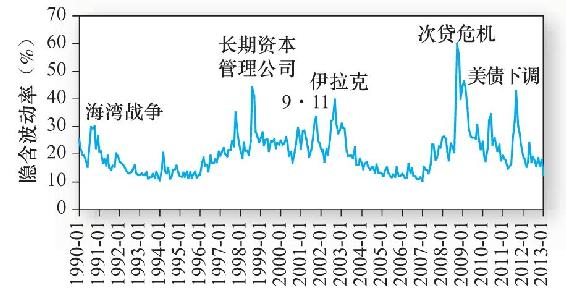
圖21-8　標準普爾500指數的隱含波動率（VIX指數）

資料來源：Chicago Board Options Exchange，www.cboe.com.

自2004年開始，標準普爾500指數30天隱含波動率期貨合約在芝加哥期權交易所開始交易。合約的收益取決於合約到期時的市場隱含波動率。合約的代碼是VIX。

隨著情況的明晰，觀察者用它來推斷未來幾個月股票的預期價格波動。在這種情況下，文章根據2012年年底進行的關於所謂“財政懸崖”的政治談判，質疑了相對較低的VIX水平。問題在於，如果和談失敗了，VIX的合約價格是否表明投資者對市場的潛在破壞過於自滿。

圖21-8也揭示了一個棘手的經驗事實。布萊克-斯科爾斯公式假定股票波動率保持不變，而從公式中計算出的隱含波動率時間序列遠非保持不變。這個矛盾提醒我們布萊克-斯科爾斯模型（像所有的模型）是一個簡化模型，並不能抓住真實市場的所有方面。在這種特定情景下，允許股票波動率有隨機性，對定價模型進行拓展是有必要的，並且事實上，沿著這個思路對模型進行的改進已有許多。^[5]

事實上，波動率變動不可預測意味著選擇恰當的波動率代入任何期權定價模型都是有困難的。最近一些重要的研究都致力於預測波動率變動的技術。這些技術，包括ARCH和隨機波動率模型，假定波動率變動是部分可預測的，並通過分析波動率的當前水平和趨勢來改進對未來波動率的預測。^[6]

概念檢查21-7

假定表21-3中看漲期權的實際售價是8美元，它的隱含波動率是大於還是小於27.83%？利用電子數據表來計算。

華爾街實戰21-2　“恐懼指數”的冰山一角

在芝加哥證券交易所（CBOE），那些在恐懼中進行交易的人看不到恐懼的存在反而很冷靜。

美國市場的波動性指標指向相對平靜，但一些投資者說，低讀數是一種自滿的跡象。不像美國總統大選後的股票震盪性波動，CBOE波動性指數，或稱VIX，表現得很平靜。四個月後，所謂的金融市場恐慌指數已經跌破其20年來的歷史平均水平，其最長的連續5年以上。

一些投資者擔心低讀數是一種自滿的跡象，而這一點在應對突發性利空消息時的潛力並沒有反映在股票價格上。這些投資者認為，關於稅收和支出方面的協議在年底即將到期，各種變化無常的指標或將走高。這種擔心也可能會反映在股票和商品市場的波動性增加上。

VIX指數是根據投資者願意支付的以標準普爾指數來計算的期權的價格來計算的。當投資者變得焦慮，他們更願意在股權上花費更多的錢，由此推動了VIX指數。

當一些市場觀察家試圖找到探求這種平靜是否會持續的線索時，一些人開始回憶2011年的夏天。當時，儘管市場人士擔心國會不同意提高債務上限，VIX交易水平仍然接近今天。這種情況可能會導致美國政府拖欠債務。

幾周內，由於對債務上限爭論不休，標準普爾下調了美國長期信用評級。在短短兩週內，波動率指數變為48，幾乎翻了3倍。

“這種情形讓我覺得整個市場缺乏一個緩衝，如果負面事件發生，這樣會導致更強烈的衝擊。”馬歇爾·帕爾默如是說，他是第一交易組的人，在國會預算委員會版進行交易。

21.4.2　股利與看漲期權定價

我們已經知道布萊克-斯科爾斯公式要求股票不支付股利，當在期權到期之前股票支付股利時，我們就要調整公式。股利的支付提高了提前執行期權的可能性，對更接近現實支付股利的情況，定價公式變得比布萊克-斯科爾斯公式更為複雜。

我可以由一些經驗規則近似求出期權價值。最初由布萊克建議的一種流行方法是將股票價格減去期權到期之前所有股利支付的現值。^[7]於是，我們就可以簡單地用S₀-PV（D）代替S₀。這樣，通過這種調整就把股利對股票價格的最終影響考慮進來了。假定期權持有至到期，則期權價值的計算方法與之前相同。

在一個特定情況下，股利調整會採取一種簡單的形式。我們假定標的資產支付連續現金收入。這一假設對股票指數期權來說是一個合理的假設，這裡不同的股票在不同日期發放股利，從而股利收入就會以或多或少的連續現金流出現。如果股利率保持不變，記為δ，到期之前累積股利的現值為S₀（1-e^-δT）。（更直觀地，注意e^-δT近似等於1-σT，所以股利的價值就近似等於δTS₀。）在這裡，S₀-PV（D）=S₀e^-δT，只要簡單地把原公式中的S₀代換成S₀e^-δT，就可以得到股利支付資產的布萊克-斯科爾斯看漲期權公式。表21-3用的就是這種方法。

對歐式看漲期權來說，這種方法能夠產生更接近的近似值，因為歐式期權必須持有至到期。但是，對美式期權這種方法就不適用了，因為美式看漲期權所有者可在股利支付之前行權。在股利支付日之前執行期權時的看漲期權價值，可能高於持有至到期時的看漲期權價值。儘管持有至到期有更長的有效時間，這會增加期權的價值，但也承擔了更多的股利支付，降低了到期日的預期股票價格，從而降低了當前的期權價值。

例如，假設股票價格為20美元，在4個月內將支付1美元股利，而該股票的看漲期權在6個月後到期。有效年利率為10%，所以股利的現值為1/（1.10）^1/3=0.97美元。布萊克建議我們可以用下面兩種方法中的任意一種來計算期權價值：

·假定提前執行，把實際股票價格20美元和4個月到期期限（股利支付的時間）代入布萊克-斯科爾斯公式計算。

·假定不會提前執行，把股利調整後股票價格20-0.97=19.03美元和6個月到期期限代入布萊克-斯科爾斯公式計算。

得出兩個值中的較大者就是對期權價值的估計，也許提前執行是最優的。換句話說，所謂的偽美式看漲期權價值（pseudo-American call option value）就是假定期權持有至到期時得到的價值和假定期權恰在除息日前執行得到的價值中的最大者。但是這種方法並不精確，因為它假定期權持有者現在就做了一個不可改變的何時行權的決策，而實際上這個決策在發出執行通知之前都不是要必須遵守的。^[8]

21.4.3　看跌期權定價

我們已經討論了看漲期權的定價。我們可以通過看跌-看漲期權平價定理得到布萊克-斯科爾斯歐式看跌期權定價公式。對看跌期權定價，我們只需簡單地根據布萊克-斯科爾斯公式求出看漲期權的價值，並求解出看跌期權的價值：

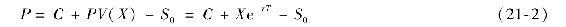
為了與布萊克-斯科爾斯公式一致，我們必須使用連續複利來計算行權價格的現值。

有時，直接使用看跌期權定價公式更加簡單。如果我們把看漲期權布萊克-斯科爾斯定價公式代入式（21-2），就可以得到歐式看跌期權的價值為：

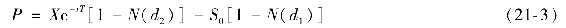
【例21-5】布萊克-斯科爾斯看跌期權定價

利用例21-2中的數據（C=13.70美元，X=95美元，S=100美元，r=0.10，σ=0.50和T=0.25），由式（21-3）可知，具有相同行權價格和到期期限的股票歐式看跌期權價值為：

注意這個值與看跌-看漲期權平價是一致的：

正如我們已經注意到的，作為交易策略的一個步驟，我們會將該計算結果與實際看跌期權價格相比較。

21.4.4　股利與看跌期權定價

式（21-2）和式（21-3）適用於不支付股利股票的歐式看跌期權。如我們對看漲期權所做的，如果標的資產支付股利，我們用S₀-PV（D）代替S₀就可以得到歐式看跌期權的價值。表21-3中單元格E7允許股利收益率δ的連續股利流，在那種情況下，S₀-PV（D）=S₀e^-δT。

但上市的美式股票期權提供了提前執行的機會，並且我們已經知道提前執行的權利是有價值的，這意味著美式看跌期權比相應的歐式期權更有價值。因此，式（21-2）和式（21-3）僅僅是美式看跌期權真實價值的下限。即便如此，這種近似的計算在很多應用中已經算是很精確的了。^[9]

[1] Fisher Black and Myron Scholes，“The Pricing of Options and Corporate Liabilities，”Journal of Political Economy 81（May-June 1973）.

[2] Robert C.Merton，“Theory of Rational Option Pricing，”Bell Journal of Economics and Management Science 4（Spring 1973）.

[3] 費舍爾·布萊克於1995年去世。

[4] 這個概念的介紹參見：Richard E.Schmalensee and Robert R.Trippi，“Common Stock Volatility Expectations Implied by Option Premia，”Journal of Finance 33（March 1978），pp.129-47.

[5] 這個領域具有影響力的文章有：J.Hull and A.White，“The Pricing of Options on Assets with Stochastic Volatilities，”Journal of Finance（June 1987），pp.281-300；J.Wiggins，“Option Values under Stochastic Volatility，”Journal of Financial Economics（December 1987），pp.351-72；and S.Heston，“A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bonds and Currency Options，”Review of Financial Studies 6（1993），pp.327-43。最近發表文章，參見：E.Ghysels，A.Harvey，and E.Renault，“Stochastic Volatility，”in Handbook of Statistics，Vol.14：Statistical Methods in Finance，ed.G.S.Maddala（Amsterdam：North Holland，1996）.

[6] 對這些模型的介紹請參見：C.Alexander，Market Models（Chichester，England：Wiley，2001）.

[7] Fischer Black，“Fact and Fantasy in the Use of Options，”Financial Analysts Journal 31（July-August 1975）.

[8] 支付股利的美式看漲期權的精確定價公式，參見：Richard Roll，“An Analytic Valuation Formula for Unprotected American Call Options on Stocks with Known Dividends，”Journal of Financial Economics 5（November 1977）.該技術得到討論與修改，參見：Robert Geske，“A Note on an Analytical Formula for Unprotected American Call Options on Stocks with Known Dividends，”Journal of Financial Economics 7（December 1979），and Robert E.Whaley，“On the Valuation of American Call Options on Stocks with Known Dividends，”Journal of Financial Economics 9（June 1981）。這些文章都很深奧。

[9] 對美式看跌期權更詳細的論述，參見：R.Geske and H.E.Johnson，“The American Put Valued Analytically，”Journal of Finance 39（December 1984），pp.1511-24.