e1 Zvi Bodie 投資學 v10
21.3 二項式期權定價
21.3.1 兩狀態期權定價
沒有堅實的數據基礎，要完全理解通常使用的期權定價公式是很困難的。但是，我們仍然可以通過一個簡單的特例來對期權定價進行有價值的考察。假定在期權到期時股票價格只有兩種可能的值：股票價格漲到給定的較高價格，或者降至給定的較低價格。雖然這可能看起來太簡單，但可以幫助我們進一步理解更復雜與現實的模型。而且，我們可以拓展此模型來描述股票價格行為更合理的特徵。實際上，幾家大型財務公司已經使用這種模型的變體來對期權與具有期權特徵的證券進行定價。
假定現在股票價格為100美元，年底的股票價格可能上漲u=1.20~120美元（u表示上漲）或者下跌d=0.9~90美元（d表示下跌）。該股票的看漲期權的行權價格為110美元，到期期限為1年，利率為10%。如果股票價格下跌，年底看漲期權持有者的收益將為零；如果上漲到了120美元，收益為10美元。
下面用“二叉樹”來闡述這些可能性，如右上圖所示。
將看漲期權的收益與一個由一股股票和81.82美元借款組成的資產組合的收益進行比較，借款利率為10%。這一資產組合的收益也取決於年底的股票價格（見下表）。
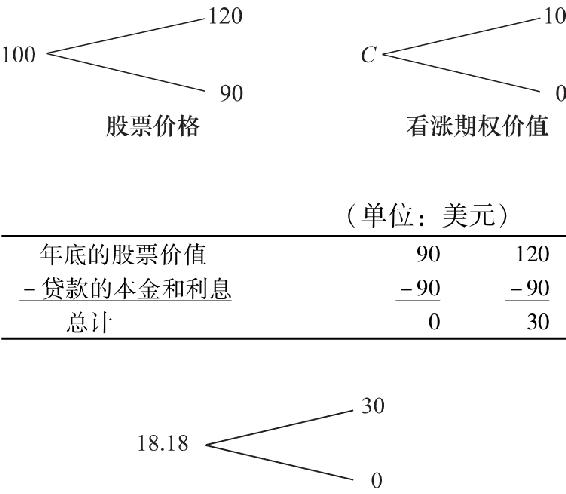
我們知道構建資產組合的現金支出是18.18美元：用來買股票的100美元減去借款得到的81.82美元。因此，這個資產組合的價值樹如右下圖所示。
不管年底股票價格是何值，這一資產組合的收益都是看漲期權收益的3倍。換句話說，三份看漲期權正好可以複製出資產組合的收益；於是三份看漲期權的價值與構建資產組合的成本相同。這樣，三份看漲期權的售價應等於資產組合的成本，即
3C=18.18美元
或者每份看漲期權的售價C=6.06美元。這樣，給定股票價格、行權價格、利率與股票價格波動性（即股票價格上漲或下跌的幅度），我們就能夠得出看漲期權的公允價值。
這種定價方法主要依賴於複製的概念。基於股票以後兩種可能的價值，槓桿化的資產組合的收益複製了三份看漲期權的收益，因此具有相同的市場價格。複製已經成為大部分期權定價公式的後盾。對於幾個分佈更復雜的股票來說，複製技術也相應地更為複雜，但原理是相同的。
我們也可以從另一個角度來考察複製的作用。仍使用前面例子的數字，由一股股票和出售三份看漲期權構成的資產組合是完全對衝的。它的年末價值不受最終股票價格的影響（見下表）。
投資者構造了一個無風險資產組合，其未來收益為90美元。它的價值一定等於90美元的現值，即90/1.10=81.82美元。資產組合的價值，等於股票多頭100美元減去賣出三份看漲期權的價值3C，應該等於81.82美元。因此100-3C=81.82美元，即C=6.06美元。
構造一個完全對衝頭寸的能力是上述論證的關鍵。對衝鎖定了年末的收益，該收益可以用無風險利率來折現。根據股票的價值得到期權的價值，我們並不需要知道期權或者股票的貝塔值與期望收益率。完全對衝或複製的方法，使我們可以用不包含這些信息的股票現值來表示期權的價值。通過頭寸對衝，最終的股票價格就不會影響投資者的收益，所以股票的風險與收益參數也不會受到任何影響。
這個例子中的對衝比率是一股股票對三份看漲期權，即1∶3。這個比率在這裡簡單解釋如下：它是期權價值的變動範圍與股價只有兩個取值時的股價變動範圍的比值。最初股票價格是S0=100美元，將來價值等於d×100=90美元，或者u×100=120美元，變動範圍為30美元。如果股票價格上漲，看漲期權價值為Cu=10美元，而如果股票價格下跌，看漲期權價值Cd=0，變動範圍為10美元。變動範圍的比率為1/3，這正是我們構造頭寸的對衝比率。
對衝比率等於變動範圍的比率，因為在這個兩狀態的例子中，期權與股票是完全相關的。當期權與股票完全相關時，完全對衝要求持有期權與股票的比例由相對波動性來決定。
對於其他兩狀態期權問題，我們給出對衝比率的一般公式
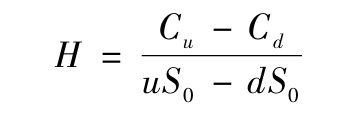
其中，Cu和Cd分別表示股票價格上漲與下跌時看漲期權的價值，uS0和dS0是兩狀態下的股票價格。對衝比率H是期權與股票期末價值波動範圍的比率。如果投資者售出一份期權，並持有H股股票，那麼該資產組合的價值將不受股票價格的影響。在這種情況下，期權定價就很容易：僅僅使對衝的資產組合的價值等於已知收益的現值即可。
利用我們的例子，期權定價技術將包括以下步驟：
（1）給定年底可能的股票價格，uS0=120和dS0=90，行權價格為110，計算得Cu=10與Cd=0。股票價格變動範圍為30，期權價格變動範圍為10。
（2）計算對衝比率為10/30=1/3。
（3）賣出一份期權與1/3股股票組成的資產組合，在年末的價值確定為30美元。
（4）年利率為10%，30美元的現值為27.27美元。
（5）讓對衝頭寸的價值等於將來確定收益的現值：
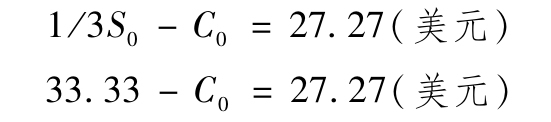
（6）解出看漲期權的期價，C0=6.06美元。
如果期權價值被高估（比如售價為6.50美元），又會如何呢？這樣你可以獲得套利利潤，具體做法如下表所示。
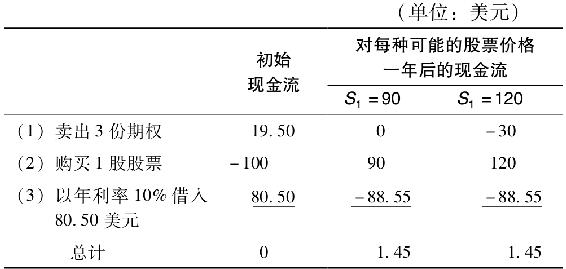
雖然初始淨投資為零，但是一年後的收益為正，並且是無風險的。如果期權被低估了，我們就會採取相反的套利策略：購買期權，出售股票，消除價格風險。另外，套利利潤的現值正好等於期權價值高估部分的3倍。利率10%，無風險利潤1.45美元的現值是1.318美元。該套利策略賣出了3份期權，給每份期權帶來0.44美元的利潤，正好等於期權價值被高估的數額：6.50美元減去公允價值6.06美元。
概念檢查21-3
假定看漲期權價值被低估了，售價為5.50美元。闡述利用錯誤股價的套利策略，並證明每購買一份期權一年後可以獲得0.6167美元的無風險現金流。比較該現金流的現值與期權價值錯估的部分。
21.3.2 兩狀態方法的推廣
雖然兩狀態股票定價模型看起來很簡單，但是我們可以將其推廣，加入現實的假設。首先，我們假定將1年分成2個6個月，然後假定在任何一個時期，股票都只有兩個可能的價值。這裡我們假定股價將上升10%（即u=1.10）或下降5%（即d=0.95）。股票的初始價格為每股100美元，在一年中價格可能的路徑如右上圖所示。中間價為104.50美元，可通過兩條途徑獲得：上升10%後下跌5%，或者下跌5%後上升10%。
這裡有三種可能的年末股票價值與期權價值，如下圖所示。
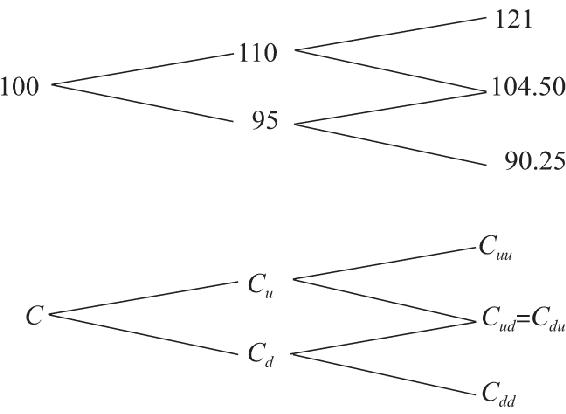
使用類似前面採用的方法，我們可以從Cuu與Cud得到Cu，然後從Cdu與Cdd得到Cd，最後從Cu和Cd得到C。而且我們也沒有理由就停止在6個月的時間間隔上，接下來我們可以把1年分成4個3個月，或者12個1個月，或者365天，每一個時間段都假定是一個兩狀態過程。雖然計算量變得很大而且枯燥，但是對計算機程序來說卻很容易，並且這種計算機程序在期權市場上得到了廣泛的應用。
概念檢查21-4
驗證例21-1中看漲期權的最初價值為4.434美元。
（1）確認期權價值的價差為Cu-Cd=6.984美元。
（2）確認股票價值的價差為uS0-dS0=15美元。
（3）確認對於每個看漲期權空頭的對衝比率為買入0.4656股。
（4）證明由0.4656股股票和一份看漲期權空頭構成的資產組合，其第一個時期價值是無風險的。
（5）計算上述組合支付的現值。
（6）求出期權價值。
【例21-1】二項式定價
假定6個月無風險利率為5%，有一個行權價格為110美元的股票看漲期權，用上述股票價格二叉樹來對此期權定價。我們首先從求Cu的價值入手。從這點開始，直到期權的到期日，看漲期權價值能上升至Cuu=11美元（因為在該點股票價格u×u×S0=121美元），或者下跌至Cud=0（因為在此點，股票價格u×d×S0=104.50美元，低於期權行權價格110美元）。因此，在該點的對衝比率為：
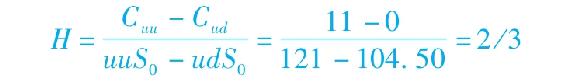
這樣，不管到期日股票價格如何，下列資產組合的價值都為209美元，如下表所示。
該組合的當前市場價值必定等於209美元的現值：
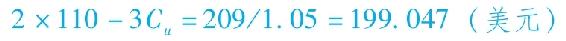
由上式可以求得Cu=6.984美元。
下一步，求Cd的價值。很容易看出其價值一定是零。如果達到這個點（相應股票價格為95美元），期權到期日股票價格將為104.50美元或90.25美元；在任何一種情況下，期權到期時處於虛值狀態。（更正式地，我們注意到在Cud=Cdd=0時，對衝比率為零，一個具有零股股票的資產組合將複製看漲期權的收益情況！）
最後，我們用Cu和Cd的值求出C的值。概念檢查21-4給出了計算C的步驟，並證明了期權的價值為4.434美元。
21.3.3 使估值模型更為實用
當我們把一年分成越來越多的時間間隔時，年末股票可能價格的範圍也隨之擴大。比如，我們將劃分的時間間隔增加至三段，股票的預期價格也變為了四種，就像在右面的這幅股票價格樹狀圖中所展示的這樣。
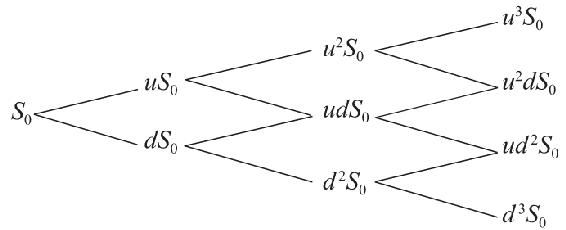
因此，通過將時間劃分為更多的時間間隔，我們能夠克服價值模型中一個很明顯的弊端：年末股票價格的數量很小。
注意，像u3S0或者d3S0這樣的極端情況是很少會發生的，因為它們需要在三個子間隔內連續增加或減少。中間範圍的，像u2dS0能通過不止一條途徑得到，任何的價格兩升一降組合將會得到u2dS0。這樣的方法有三種：uud，udu，duu。相反，只有uuu一種方法能夠實現u3S0的股票價格。因此，中間範圍的值可能性更大一些。當我們把模型變得更為接近實際，並且將期權到期日之前的這段時間劃分為越來越多的子時間段時，股票最終的價格分佈開始呈現出類似鐘形的曲線，涵蓋了極不可能出現的極端情況和很有可能出現的中間值的情況。用二項式分佈可以將每個結果的概率描述出來，因此這種多時期的期權定價方法被稱為二項式模型（binominal model）。
但是我們仍然需要回答一個很重要的現實問題。在把二項式模型應用於評估真實的期權之前，我們需要給u和d賦一個合理的值，股票價格的上下波動反映了其回報率的不確定性，所以u和d的數值的選擇就取決於這種不確定性。設股票回報率的年標準差為σ，Δt為每個子間隔的時間長度，為了使二項式模型中的標準差符合你估計的σ，可以設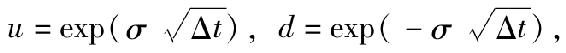
[1]可以看到，隨著年度的波動以及子間隔的變化，u和d之間的差異逐步變大。這一發現很有意義，更高的σ值和更長的持有期間使得股票的價格更加不確定。下面的這個例子闡述瞭如何應用這一原理。
【例21-2】根據股票波動性來校準u和d
假設你正在用三個時間間隔的模型來計算1年期的股權價格，年標準差為σ=0.3，到期日為T=1年，三個子時間間隔，你會計算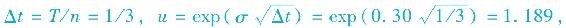
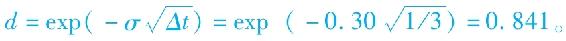
考慮到一個股票上升的概率，你可以計算出任何股票最終價值的概率。例如，假設股票價格上漲的概率為0.554，下降的概率是0.446（注：在這種情況下，股票的預期回報率為0.1，總之，年期望收益率為r的股票價格上升的概率為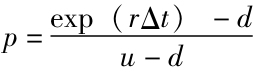
），年末股票的預期價格如下表：
我們在圖21-5的曲線a中展示了這種分佈。注意，兩個中間階段的股票事實上比極端情況發生的可能性更大。
現在，我們可以通過將到期期間劃分為更短的時間間隔來把21-2進行拓展。正如我們在例21-3中所研究的那樣，股票價格分佈變得越來越有可能。
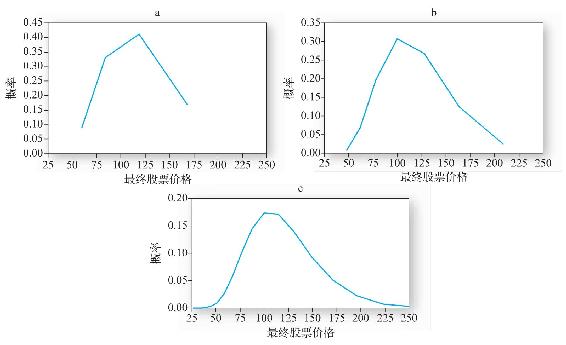
圖21-5 最終股票價格的概率分佈：可能出現結果及其相應概率，每條曲線中，股票的年綜合期望收益為10%，標準差為30%。a曲線為3個間隔：在每個間隔，股票上漲18.9%或下降15.9%；b曲線為6個間隔：在每個間隔，股票上漲13.0%或下降11.5%；曲線c為20個間隔：在每個間隔，股票上漲6.9%或下降6.5%
【例21-3】增加時間間隔的數量
在例21-2中，我們把一年分為3個階段，我們現在來看一下，當劃分為6個和20個時間間隔時的情況如何。
我們在圖21-5[2]的b和c中展示了這種結果。
注意，曲線c的右側明顯長於左側。事實上，隨著間隔數量的增加，分佈逐步接近歪斜的對數正態分佈（而不是對稱的正態分佈）。即使股票價格下降，在每個子區間，它永遠不可能降到0以下，但其潛在性能沒有相應的上限。這種不對稱性產生了分佈的偏態。
最後，隨著我們將持有期分成越來越小的間隔，每個事件樹的節點對應著無限小的時間間隔，那麼在這些時間間隔內股票價格的變動相應地也非常小。隨著時間間隔的增加，最後股票價格越來越接近於對數正態分佈。[3]這樣，兩狀態模型過於簡化的缺點就可以通過時間間隔的進一步細分來克服。
在任何一個節點上，都可以構造一個在下一個時間間隔被完全對衝的資產組合。接著，在下一個時間間隔末，到達下一個節點時，又可以重新計算對衝比率，對資產組合的構成進行更新。通過不斷改變對衝頭寸，資產組合總可以保持在被對衝的狀態，在每個間隔都獲得無風險收益。這稱為動態對衝，也就是隨時間不斷調整對衝比率。動態對衝越來越完善，期權的定價過程也越來越精確。
概念檢查21-5
當期權處於深度實值時，對衝比率是越大還是越小？（提示：記住對衝比率是期權價格變化與股票價格變化的比率。什麼時候期權價格對股票價格的變動更敏感？）
華爾街實戰21-1 風險中性簡述
我們在本章前面指出，二項模型估值方法是以套利為基礎的。我們可以通過複製它與股票加上借貸的方式來評估股票期權，這種期權的能力意味著它的價格相對於股票和利率必須是基於複製的技術，而不是風險偏好。它不能依賴於風險厭惡或資本資產定價模型或任何其他模型的均衡風險收益關係。這種觀點認為，定價模型必須是獨立的風險厭惡導致一個非常有用的快捷方式來評估期權。想象一個風險中性的經濟體，即所有的投資者都是風險中性的。這種假設的經濟體必須與我們的實際價值相同，因為風險厭惡不影響估值公式。
在風險中性的經濟中，投資者不會要求風險溢價，因此評估所有資產將按無風險利率折現期望收益。因此，一個證券，如看漲期權，將利用無風險利率來貼現其預期的現金流來評估其價值：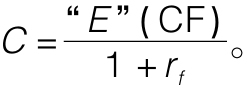
我們用“E”來表示期望值是為了強調這不是真正的期望值，而是假設風險中性經濟中的期望。為了前後保持一致，我們必須使用風險中立時的股票回報率而不能使用真實的回報率。但是如果我們成功地保持了這種一致性，假設經濟的價值應該適用於我們自身。
在風險中性的經濟中，我們如何計算出預期現金流呢？因為沒有風險溢價，股票的預期收益率必然等於無風險報酬率。股票上漲的可能性記作p，然後p必須等於股票價格上升到無風險利率時的期望利率（我們忽略股息）：
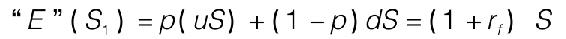
這表明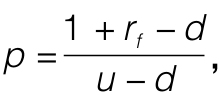
我們將p稱為風險中性的概率來將它和實際概率加以區分。為說明這一點，在21.2的開篇，我們令u=1.2，d=0.9，rf=0.1，考慮到這些值後，
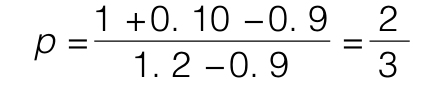
現在我們來看一下，當我們用折現公式來計算風險中立經濟中的期權價值時，會發生什麼。我們繼續沿用21.2中的例子，在無風險利率的中性概率和貼現率下，我們發現期權收益現值為：
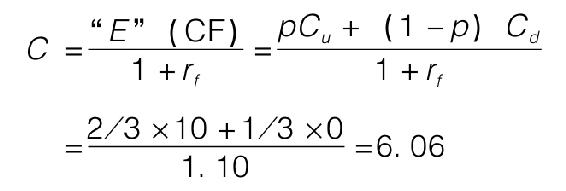
這一答案完全匹配我們的無套利方法。
我們重申：這不是一個真正的預期折現值。
·分子不是期權真正的預期現金流量，因為我們所使用的風險中性概率p不是真正的概率；
·因為我們不考慮風險，所以對期權使用了不恰當的折現率；
·從某種意義上來說，這兩個偏差相抵消了，但這不僅僅是運氣好：我們得到的是正確的結果，因為沒有套利的方法意味著風險偏好不能影響期權價值。因此，風險中性經濟的價值計算必須與我們經濟中的價值相等。
當我們進入與現實更接近的多期模型時，計算較為煩瑣，但思路是一樣的。之前的註釋說明了如何將p與任何預期的收益率和波動率估計數聯繫到一起。簡單地將股票的預期收益率設定為無風險利率，利用由此產生的概率，從期權的預期收益中，按無風險利率貼現，你能夠計算出期權價值。這些計算在Excel中實際上是相當容易實現的。
[1] 注意到，此時d=1/u，這是最常見的形式，但並非唯一的方式來校準模型的經驗波動率。替代性方法，見Robert L.McDonald，Derivatives Markets，3rd ed.，Pearson/Addison-Wesley，Boston：2013，Ch.10。
[2] 為使圖21-5中的分佈具有可比性，我們在之前的註釋中調整了概率和股票價格下跌時的公式，每條曲線中的p都代表股票的預期年收益率，複合收益率為10%。
[3] 實際上，這裡引入了更復雜的考慮。只有我們假定股票價格連續變動，也就是說在很小的時間間隔內股票價格僅發生很小的變動時，這一過程的極限才是對數正態分佈。這排除了極端事件（如公司接管）引起的股票價格異常變動。對這類問題的處理，參見：John C.Cox and Stephen A.Ross，“The valuation of Options for Alternative Stochastic Processes，”Journal of Financial Economics 3（January-March 1976），pp.145-66，or Robert C.Merton，“Option Pricing When Underlying Stock Returns Are Discontinuous，”Journal of Financial Economics 3（January-March 1976），pp.125-44.