e1 Zvi Bodie 投資學 v10
21.2 期權價值的限制
期權定價方面有很多數量模型,在本章中我們將考察其中一部分模型。但是,所有這些模型都建立在簡化的假設之上。你可能想知道期權價值的性質中哪些是普遍適用的,哪些依賴於特定的簡化。首先,我們將探討期權價格重要的普遍性質。某些性質在股票股利支付對期權價值的影響與美式期權提前執行的可能盈利方面具有重要含義。
21.2.1 看漲期權價值的限制
對看漲期權價值最明顯的限制是其價值不可能為負。因為期權並不一定執行,它不會給持有者強加任何義務。進一步講,只要執行期權可能獲得利潤,期權就會有一個正的價值。期權的收益最差時為零,而且有可能為正,所以能夠帶來一定的收益。
我們可以給看漲期權的價值劃定另一個界限。假定股票在到期日之前的時刻T(現在為0時刻)支付D美元的股利。現在比較兩個資產組合,一個包括一份股票看漲期權,而另一個是由該股票和數額為(X+D)/(1+rf)T的借款組成槓桿化的股票頭寸。在期權到期日那天,還付貸款(X+D)美元。例如,一個行權價格為70美元的半年期期權,股利支付為5美元,有效年利率為10%,那麼在購買一股股票的同時,需借入75/(1.10)1/2=71.51美元。6個月後,歸還到期貸款75美元。
到期時槓桿化的股票頭寸的收益如下表所示。

其中,ST表示在期權到期時的股票價格。注意到股票的收益等於不含股利的股票價值加上收到的股利。股票加借款頭寸的總收益是正或負,取決於ST是否超過了X。建立槓桿化的股票頭寸的淨現金支出是(S0-71.51)美元,或者更一般地,[S0-(X+D)/(1+rf)T]也就是當前股票價格S0減去初始借款額。
如果期權到期時處於實值狀態,看漲期權的收益為(ST-D),否則為零。在期權收益與槓桿化的頭寸收益均為正時,兩者收益相等,而當槓桿化的頭寸收益為負時,期權收益高於槓桿化頭寸的收益。因為期權收益總是高於或等於槓桿化頭寸的收益,所以期權價格必須超過建立該頭寸的成本。
於是,看漲期權的價值必須高於[S0-(X+D)/(1+rf)T],或者更一般地:
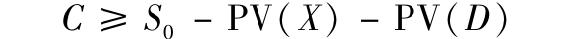
式中,PV(X)表示行權價格的現值,PV(D)表示期權到期時股票支付股利的現值。更一般地,我們把PV(D)解釋為期權到期日之前所有股利的現值。由於已知看漲期權的價值為非負,所以可知C大於等於0和[S0-PV(X)-PV(D)]兩者中的最大值。
我們還可以劃定期權價值的上限,這個上限就是股票的價格。沒有人會支付高於S0美元的金額去購買價值為S0美元的股票的期權。因此,有C≤S0。
圖21-2給出了看漲期權價值所處的範圍,該範圍由上述的上限和下限決定。根據我們得到的期權價值的限制,期權價值不可能處於陰影區域之外。期權到期之前,看漲期權的價值在陰影區域之內,但是不會達到上下邊界,如圖21-3所示。
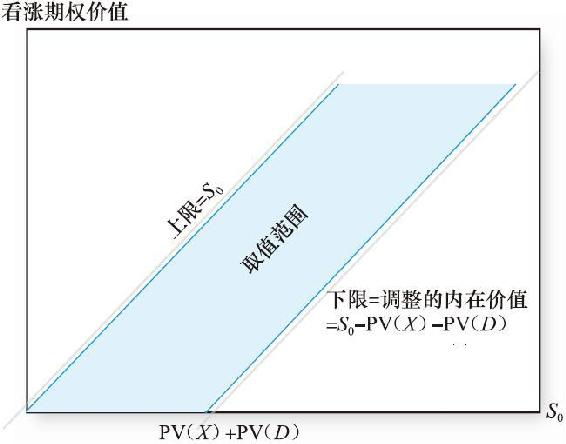
圖21-2 看漲期權價值所處的可能範圍
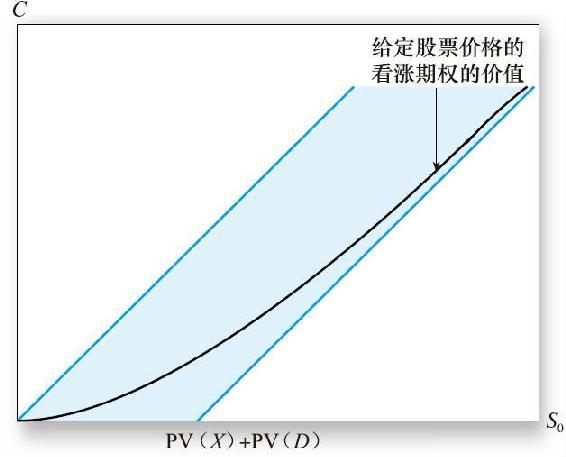
圖21-3 看漲期權價值與股票現價之間的函數關係
21.2.2 提前執行期權與股利
想平掉頭寸的看漲期權持有者有兩種選擇:執行期權或將其出售。如果持有者在t時刻執行期權,獲得收益為(St-X),假定期權處於實值狀態。我們已經知道,期權最低可以[St-PV(X)-PV(D)]的價格賣出。因此對不支付股利的股票期權,C高於[St-PV(X)]。因為X的現值小於X本身,所以有:
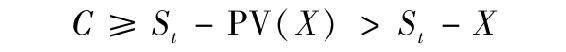
這意味著以價格C出售期權的收益一定大於執行期權的收益(St-X)。從經濟角度講,出售期權要比執行期權更具有吸引力,這可以讓期權繼續存在而不是使其消失。換句話說,對不支付股利的股票看漲期權而言,“活著比死更有價值”。
如果在到期日之前執行期權無法帶來收益,那麼提前執行就毫無價值。因此,我們可以認為對不支付股利的股票而言,美式看漲期權與歐式看漲期權是等價的。歐式看漲期權僅有一個執行時間,並且適用於歐式看漲期權的定價公式,也適用於美式看漲期權,這樣情況就簡單多了。
由於大多數股票是支付股利的,你可能想知道這一結果是否僅具有理論價值。並不是的,如果仔細加以考慮,你會發現實際上我們僅要求期權到期日之前不支付股利。對大多數期權而言,現實情況確實如此。
21.2.3 美式看跌期權的提前執行
對於美式看跌期權而言,肯定會有提前執行而達到最優的可能性。我們通過一個簡單的例子來加以說明。假如你購買一個股票的看跌期權,不久公司破產,股票價格變為零。當然,你想現在立即執行期權,因為股票價格已經不可能再跌了。立即執行意味著你接受行權價格,這可以讓你重新投資獲利。推遲執行意味著損失資金的時間價值。在到期日之前執行看跌期權的權利是一定有價值的。
現在假定公司只是瀕臨破產,股票售價僅為幾美分。立即執行期權仍是最優的選擇。畢竟,股票價格僅有幾美分的下跌空間,這意味著將來執行期權不過比現在執行期權多得到幾美分的收益。要在可能多獲得的很少的收益與推遲執行帶來的資金時間價值的損失之間進行權衡。顯然,當股票價格低於某個值時,提前執行是最優的選擇。
從以上論述可知,美式看跌期權要比相應的歐式看跌期權價值更高。美式看跌期權允許你在到期日之前的任何時間行權。因為提前執行在某些情形下可能有用,這會在資本市場上獲得一個溢價。於是,在其他條件相同時,美式看跌期權的價格高於歐式看跌期權。
圖21-4a給出了美式看跌期權的價值與股票現價S0之間的函數關係。一旦股票價格跌破臨界值,圖中記為S*,執行就是最優的選擇。在這一點,期權價格曲線與代表期權內在價值的直線相切。當股票價格達到S*時,看跌期權被執行,其收益等於期權的內在價值。
概念檢查21-2
根據以上討論,解釋為什麼看跌-看漲期權平價關係只對不支付股利的歐式股票看跌期權成立。如果股票不支付股利,為什麼美式期權不滿足該平價關係?
作為對比,如圖21-4b中的歐式看跌期權的價值並不漸近於內在價值線。因為歐式期權不允許提前執行,所以歐式看跌期權價值的最大值是PV(X),發生在S0=0時。顯然,對於足夠長的橫軸,PV(X)可以任意小。
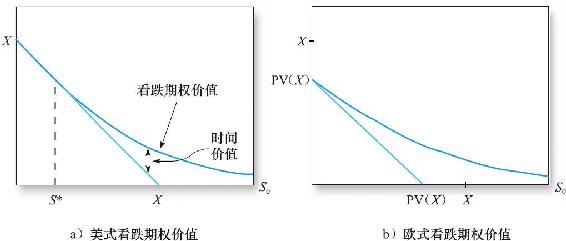
圖21-4 看跌期權價值與目前股票價格的函數