e1 Zvi Bodie 投資學 v10
20.6 金融工程
期權的魅力在於它能創造出不同的投資頭寸,其收益取決於其他證券的價值。20.4節中的各種期權策略就是我們所見的證據。
期權也可用來設計風險模式與標的證券價格具有某種關係的,且符合特定要求的新證券或資產組合。這樣,期權(與將在第22、23章討論的期貨)促進了金融工程的發展,創造了特定收益模式的資產組合。
一個簡單運用期權的產品是指數掛鉤存單(index-linked CD)。指數掛鉤存單能讓散戶做小頭寸的指數期權。不同於支付固定利息的傳統存單,指數掛鉤存單是將某個市場指數(如標準普爾500指數)收益率以特定比例回報支付給存款人,這樣即使在市場下跌時也能保證最低收益率。例如,在上漲時,指數存單支付收益的70%,在下跌時保證沒有損失。
很顯然,指數掛鉤存單實際上是一種看漲期權,在市場上漲時,存款人根據參與比率或乘數獲得利潤,在上述例子中參與比率是70%;在市場下跌時,保證投資者沒有任何損失。也很明顯,銀行提供這種存單就是在出售看漲期權,需要在期權市場購買看漲期權來對衝風險。圖20-14是銀行對存款人義務的本質。
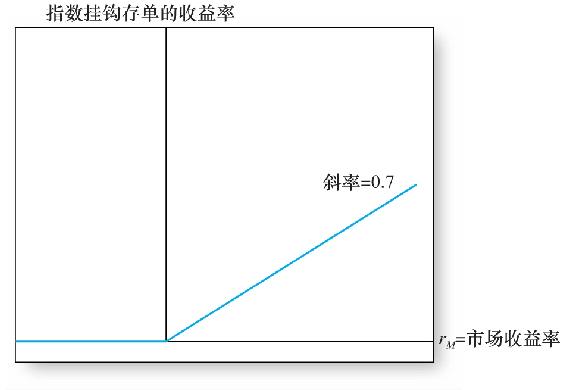
圖20-14 指數掛鉤存單的回報
銀行如何設定恰當的乘數呢?要回答這個問題,首先看一下期權的幾個特徵:
·存款人為期權支付的價格就是所放棄的傳統存單的利息。因為利息總是在期末收到,所以投資1美元利息的現值就是rf/(1+rf)。因此,存款人用一筆確定的錢,即1美元利息的現值rf/(1+rf)去投資來獲取收益,而收益取決於市場的表現。相反,銀行用本應該支付傳統存單的利息來保證履行義務。
·我們所描述的期權是平價期權,即行權價格等於現在市場指數的價格。一旦市場指數超過了合約簽訂時的價格,期權就成了實值期權。
·我們可以用1美元的投資為基礎進行分析。例如,投資1美元於指數掛鉤存單的期權成本為rf/(1+rf),期權的市場價值為C/S0:平價期權的成本為C美元,1單位市場指數價值為S0。
現在很容易就可以確定銀行提供存單的乘數。存款人每投資1美元,銀行得到rf/(1+rf)的收益。對市場指數1美元的投資,銀行需要購買的看漲期權的成本為C/S0。因此,如果rf/(1+rf)是C/S0的70%,那麼對於1美元的投資,銀行至多能夠購買0.7份看漲期權,於是乘數就是0.7。一般情況下,存單的均衡乘數為rf/(1+rf)除以C/S0。
【例20-7】指數掛鉤存單
假設rf=6%每年,6個月的市場指數的平值看漲期權的價值為50美元,市場指數為1000點,於是每1美元市場價值的期權成本為50/1000=0.05美元。6個月存單的利率為3%,這意味著rf/(1+rf)=0.03/1.03=0.0291。因此,乘數為0.0291/0.05=0.5825。
指數掛鉤存單有幾種變體。投資者可以購買類似的存單來保證得到正的最低收益,如果他們願意接受較小的存單乘數。在這種情況下,存款人購買期權的成本為每1美元投資(rf-rmin)/(1+rf)美元,其中rmin是保證得到的最低收益率。因為買價低了,買到的期權數量減少,所以乘數就變小了。另一種變體是熊市存單(bear CD),投資者也會得到市場指數一定比例的跌幅。例如,熊市存單將標準普爾500指數任何百分比跌幅的60%提供給存款人。
概念檢查20-9
仍假設半年期利率rf=3%,平值看漲期權賣價為50美元,市場指數為1000點。保證最低收益率為0.5%的6個月牛市股權掛鉤存單的乘數是多少?