e1 Zvi Bodie 投資學 v10
20.4 看跌-看漲期權平價關係
從前面的內容可知,一個保護性看跌期權組合,包括股票頭寸和與該頭寸對應的看跌期權,該組合能保證最低收益,但沒有限定收益上限。它並不是獲得這種保護的唯一方式,看漲期權加國債的組合也能鎖定風險下限,但不限定收益上限。
考慮這樣的策略,購買看漲期權,同時購買面值等於看漲期權行權價格的國債,兩者到期日相同。例如,如果看漲期權行權價格為100美元,則每份期權合約(每份合約100股股票)執行時需要支付10000美元,因此你所購買的國債的到期價值也應為10000美元。更一般地,對你所有持有的行權價格為X的期權,你需購買面值為X的無風險零息債券。
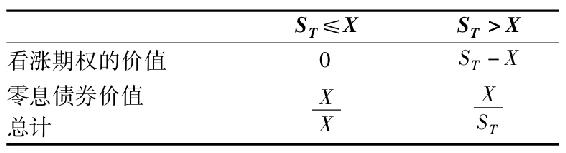
T時刻,當期權與零息債券到期時,組合的價值為:
如果股票價格低於行權價格,則看漲期權價值為零,但是無風險債券到期時等於其面值X,於是債券的價值是該組合價值的下限。如果股票價格超過X,則看漲期權的收益是(ST-X),與債券面值相加得ST。該組合的收益與表20-1中保護性看跌期權的收益是完全相同的。
如果兩種資產組合的價值總是相等的,則其成本也必須相等。因此,看漲期權加債券的成本等於股票加看跌期權的成本。每份看漲期權的成本為C,無風險零息債券的成本為X/(1+rf)T,因此,看漲期權加債券資產組合的成本為C+X/(1+rf)T。零時刻股票成本,即現在的股票價格為S0,看跌期權的成本為P,於是有:

式(20-1)稱為看跌-看漲期權平價定理(put-call parity theorem),因為它代表看漲期權與看跌期權價格之間恰當的關係。如果這個關係被違背,就會出現套利機會。例如,你搜集了某個股票的如下數據:

我們可以利用式(20-1)來驗證它是否違背了平價關係:
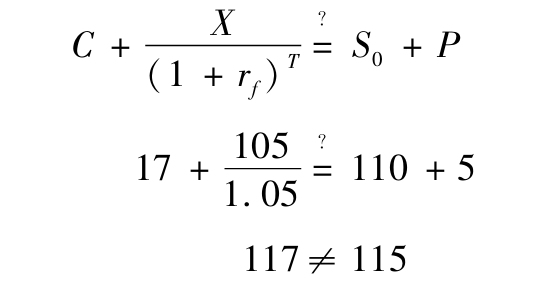
結果是違背了平價關係,117不等於115,這說明存在價格錯估。為了利用這個價格錯估,你買入相對便宜的資產組合(股票加看跌期權組合,等式右邊),並賣出相對昂貴的資產組合(看漲期權加債券組合,等式左邊)。因此,如果你買入股票,買入看跌期權,賣出看漲期權並借入100美元1年(因為借入資金是購買債券的相反行為),就可以獲得套利利潤。
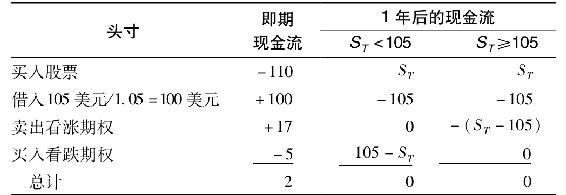
來看一下這個策略的收益。1年後,股票價格價值為ST,100美元的借款要還付本息,即現金流出105美元。如果ST超過105美元,賣出看漲期權會導致現金流出(ST-105美元)。如果股票價格低於105美元,買入看跌期權的收益為(105美元-ST)。
表20-5是對結果的總結。現在的現金流為2美元,1年後,各個頭寸的現金流互相抵消了,也就是說實現了2美元的現金流入但是沒有相應的現金流出。投機者都會追求這種套利利潤,直到買賣的壓力使式(20-1)表達的平價關係滿足為止。
表20-5 套利策略
式(20-1)實際上只適用於在期權到期日前股票不分發股利的情況,但可以很直接地將其推廣到股票支付股利的歐式期權情況。本章節最後的第12題將會證實這一點。看跌期權與看漲期權平價關係更一般的公式是:
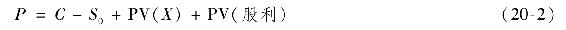
其中,PV(股利)表示在期權有效期內收到股利的現值。如果股票不支付股利,則式(20-2)就變成式(20-1)。
注意這個一般公式也適用於除了股票外其他資產為標的物的歐式期權。我們只需讓該資產在期權有效期內的收益代替式(20-2)中的股利。例如,債券的看跌期權與看漲期權就滿足同樣的平價關係,只是債券的息票收入代替了公式中股票的股利。
但是這個一般化公式只適用於歐式期權,並且只有在每個頭寸都持有到到期時,式(20-2)兩邊代表的兩種資產組合的現金流才會相等。如果看漲期權和看跌期權在到期日前的不同時間被執行,則不能保證兩邊的收益是相等的,甚至也不能保證期望收益相等,這樣兩種資產組合會有不同的價值。
【例20-6】看跌期權與看漲期權平價
利用圖20-1中IBM期權的數據,我們看一下平價關係是否成立。1月到期的看漲期權行權價格為195美元,距離到期日28天,價值為3.65美元,相應的看跌期權價值為5美元。IBM股票價格為194.47美元,短期年化利率為0.1%。2月8日為除權日,IBM公司需要在18天的時間裡支付0.85美元的股利。根據平價關係,我們發現有
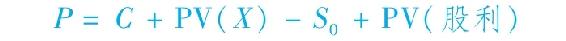
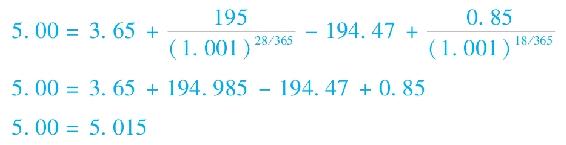
平價關係不滿足,並且出現了每股0.015美元的偏差。這個偏差大到可以利用的程度了嗎?幾乎可以肯定地說,並沒有。你必須權衡潛在的利潤能否彌補看漲期權、看跌期權與股票的交易成本。更重要的是,在期權交易並不頻繁的事實情況下,與平價的偏差可能並不是“真的”,可能僅是由於“陳舊”的報價造成的,而你已不可能在此價格上進行交易了。