BUSINESS BOOKS

概念檢查答案

16-1　使用表16-3，每半年付息一次，貼現率4.5%。

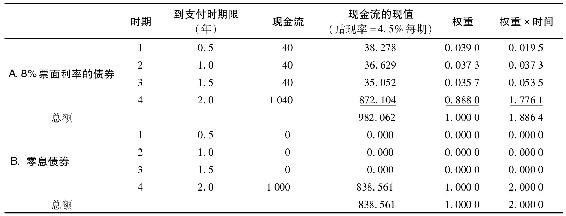
8%票面利率債券的久期增加到1.8864年。價格上漲至982.062美元。到2年時，零息債券的久期不變，儘管當利率降低時，價格會上升（至838.561美元）。

16-2　a.如果利率從9%上升至9.05%，那麼債券價格從982.062美元下跌至981.177美元。價格變化百分比是-0.0901%。

b.使用初始半年利率4.5%，久期為1.8864年（參見概念檢查16-1），所以久期公式預測的價格變化為：

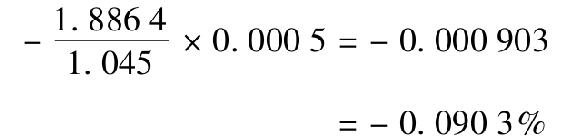
這與a中直接計算得到的答案几乎相同。

16-3　終身年金的久期為（1+y）/y或者是1+1/y，當y增加時，顯然會下降。把久期作為y的函數，我們得到：

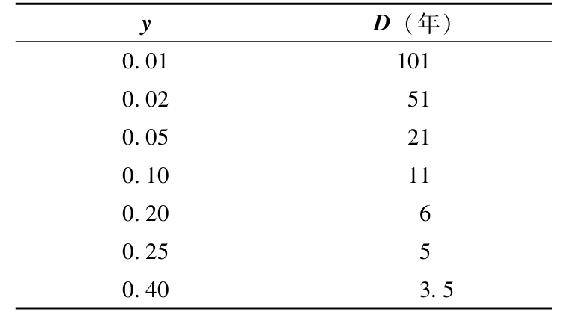
16-4　根據本章所述的久期法則，當票面利率和到期收益率較高時，你應該發現久期較短。對大多數債券而言，久期隨著到期期限增加而增加。當票面利率是半年支付一次而不是一年一次時，久期下降，因為平均而言，支付發生較早。不是等到年底才收到年利息，投資者在半年的時候就收到了一半利息。

16-5　麥考利久期定義為債券全部現金流發生時間的加權平均。修正久期定義為麥考利久期除以1+y（其中y為每次支付時的收益率，例如，如果債券每半年支付一次利息，y就是半年的收益率）。這表明對普通債券而言，修正久期等於債券價格變化率比收益率的變化量。有效久期抓住了修正久期的這一最後特徵。它被定義為債券價格變化率與市場利率變化量之比。關於嵌入期權債券的有效久期，在計算價格變化時，需要一種考慮這些期權的定價方法。此時計算有效久期不能用對現金流的發生時間進行加權平均的方法，因為這些現金流是隨機的。

16-6　終身年金的久期現在為1.08/0.08=13.5。我們需要解下列關於w的方程：

w×2+（1-w）×13.5=6

因此，有w=0.6522。

16-7　貢獻策略更具有吸引力。現金流匹配免除了再平衡的需要，於是就節約了交易費用。

16-8　當前價格=1091.29（美元）

預測價格=100×年金因子（10%，18年）+1000×現值因子（10%，18年）=1000（美元）

再投資利息的終值是：（100×1.08）+100=208（美元）

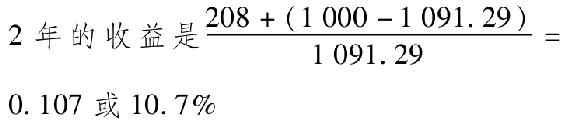
那麼，2年期間的年化收益率將是（1.107）^1/2-1=0.052或5.2%。