e1 Zvi Bodie 投資學 v10
16.1 利率風險
我們知道債券價格與其收益之間存在反向關係,並且我們也知道利率會有大幅波動。隨著利率的漲跌,債券持有人會有資本利得和損失。這些利得和損失使得固定收益投資具有風險性,即便利息和本金支付有保障,例如國債。
為什麼債券價格會對利率波動做出反應?需要記住的是,在競爭市場中所有證券給投資者的期望收益率應該是相當的。當債券發行的票面利率是8%,而市場的競爭性收益率也是8%時,債券將以面值出售。但是,如果市場利率升至9%,那麼還有誰會以面值來購買利率為8%的債券呢?這時債券價格一定會下跌,直到它的期望收益率上升至具有競爭力水平的9%為止。相反,如果市場利率下跌至7%,相對於其他投資的收益而言,這種票面利率為8%的債券會更具吸引力。於是,渴望得到這種收益的投資者會抬高債券價格直到高價購買債券的人獲得的總收益率不再高於市場利率。
16.1.1 利率敏感性
債券價格對市場利率變化的敏感性對投資者而言顯然十分重要。為深入瞭解利率風險的決定因素,可以參見圖16-1。該圖表示了票面利率、初始到期收益率和期限互不相同的四種債券,當到期收益率變化時,債券價格相應的百分比變動。所有這四種債券都表明,當收益率增加時,債券價格下降,並且價格曲線是凸的,這意味著收益下降對價格的影響遠遠大於相同程度收益增加對價格的影響。我們將這些性質歸結為以下兩點:
(1)債券價格與收益成反比:當收益升高時,債券價格下跌;當收益下降時,債券價格上升。
(2)債券的到期收益率升高導致其價格變化的幅度小於等規模的收益下降導致其價格變化的幅度。
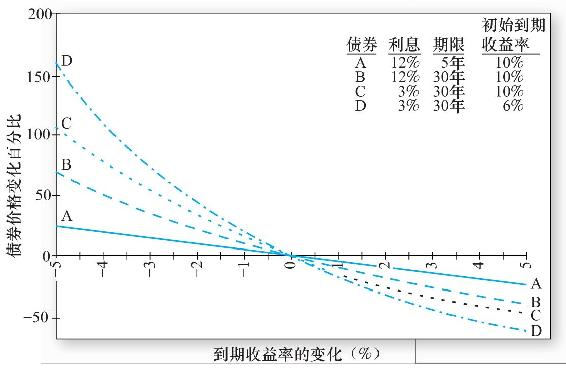
圖16-1 作為到期收益率變化的函數的債券價格變化
現在,比較債券A和B的利率敏感性,除到期時間外,其他參數均相同。圖16-1表明債券B比A期限更長,對利率更敏感。這體現出另一基本性質。
(3)長期債券價格對利率變化的敏感性比短期債券更高。
這不足為奇。例如,如果利率上漲,由於現金流以更高的利率水平貼現,則債券的價值會有所降低。越是遠期的現金流,提高貼現率的影響會越大。
值得注意的是,當債券B的期限是債券A的期限的6倍時,它的利率敏感性卻比債券A大不了6倍。儘管利率敏感性隨到期時間延長而增加,但卻不是按到期日延長的比例增加的。因此,我們有了第四條性質。
(4)當債券期限增加時,債券價格對收益率變化的敏感性增加,但增速遞減。換句話說,利率風險變動小於債券期限變動。
債券B和C,除票面利率之外,其他參數均相同,這時表現出另一特徵。票面利率較低的債券對市場利率變化更敏感。這體現出債券價格的一個普遍性質。
(5)利率風險與債券票面利率成反比。低票面利率債券的價格比高票面利率債券的價格對利率變化更敏感。
最後,債券C和D,除債券的到期收益率之外,其他參數均相同。債券C具有更高的到期收益,對收益變化的敏感性更低一些。這樣,可以得到最後一個性質。
(6)債券價格對其收益變化的敏感性與當期出售債券的到期收益率成反比。
前五條性質曾被馬爾基爾[1]所論證,有時被稱為馬爾基爾債券定價關係。第六個性質被霍默和利伯維茨[2]論證。
期限是利率風險的主要決定因素。但是,期限本身不足以測度利率的敏感性。例如,債券B和C(見圖16-1)的期限相同,但是較高票面利率的債券對利率變化有著較低的價格敏感性。顯而易見的是,我們不能僅靠債券期限來量化其利率風險。
為理解票面利率或到期收益率等債券特徵為什麼會影響利率敏感性,我們從一個簡單的數字實例開始討論。表16-1提供了不同到期收益率和期限為T的半年票面利率為8%的債券價格。其中,利率表示為年百分率(APR),即將半年收益率翻倍,以獲得約定的年化收益率。當利率從8%上升至9%時,最短期限債券的價值下跌小於1%,10年期債券下跌6.5%,而20年期債券下跌9%以上。
表16-1 票面利率為8%的債券價格(半年付息一次)
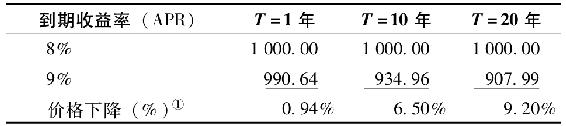
①到期收益率為9%的等值債券除以(初始)收益率為8%的債券,再減去1。
表16-2 零息債券價格(半年計一次複利)
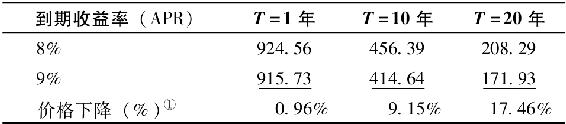
①到期收益率為9%的等值債券除以(初始)收益率為8%的債券,再減去1。
讓我們現在來看看類似的例子,不過這次不是票面利率為8%的債券,而是零息債券,結果見表16-2。請注意,對於每種期限,零息債券價格的下降比例大於票面利率為8%的債券。因為我們知道長期債券比短期債券對利率變動更為敏感,所以這一觀察表明,在某種意義上,零息債券代表一個期限更長的債券,而不是期限相同的息票債券。
實際上,這種對有效期限的洞察力對我們進行數學上的精確計算是十分有用的。首先,注意在此例中兩隻債券的期限並非債券長期與短期特徵的準確度量。票面利率為8%的20年期債券有多次利息支付,其中大部分是在債券到期之前進行的。每次支付都可以認為有它自己的“到期日”。在前面章節中,我們曾把息票債券看作息票支付的資產組合,這是十分有用的。因此,債券的有效期限是所有現金流的某種平均到期時間。相比較而言,零息債券只在到期時進行一次支付。因此,它的到期時間是一個明確的概念。
較高票面利率債券價值的很大部分與息票緊密聯繫,而不是與最終支付的票面價值相聯繫。所以,“息票資產組合”傾向在較早、短期支付上賦予更大的權重,它導致息票債券的“有效期限”較短。這解釋了馬爾基爾提出的第五個性質,即價格敏感性隨票面利率而下降。
相似的邏輯可以解釋第六個性質,價格敏感性隨到期收益率上升而下降。較高的收益降低了所有債券償付的現值,對較遠期償付而言,情況更是如此。因此,在收益較高的情況下,債券價值的較大部分來自其較早的支付。較早的支付具有較低的有效期限和利率敏感性。於是,債券價格對收益變化的整體敏感性就較低。
16.1.2 久期
為了解決債券多次支付的“期限”含糊不清的問題,我們需要一種測度債券發生現金流的平均期限的方法。我們也可以使用此方法來測量債券對利率變化的敏感性,因為我們知道價格敏感性會隨到期期限的增加而增大。
弗雷德裡克·麥考利[3]把有效期限概念定義為債券久期。麥考利久期(Macaulay’s duration)等於債券每次息票或債券本金支付時間的加權平均。每次支付時間相關的權重都應當與該次支付對債券價值的“重要性”相聯繫。實際上,每次支付時間的權重應該是這次支付在債券總價值中所佔的比例。這個比例正好等於支付的現值除以債券價格。
權重wt與在時間t所發生的現金流(標註為CFt)有關,表示為:
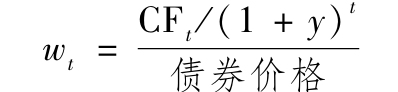
式中,y代表債券到期收益率。公式右邊的分子代表在時間t所發生現金流的現值,分母代表債券所有支付的值。這些權重的和為1.0,因為以到期收益率貼現的現金流總額等於債券價格。
用這些值來計算所有債券支付時間的加權平均,就可以得到麥考利久期公式,表示為:

作為公式(16-1)的應用,在表16-3中可以得到票面利率為8%的付息債券和零息債券的久期,兩種債券都是2年期。假設到期收益率均為10%,或半年5%。B欄中顯示週期(半年)的每次支付的貼現率為5%。每次支付期限(F欄)的權重等於該時點的支付現值(E欄)除以債券價格(E欄中的現值總額)。
表16-3 計算兩種債券的久期(欄中的總額遵從化整誤差)
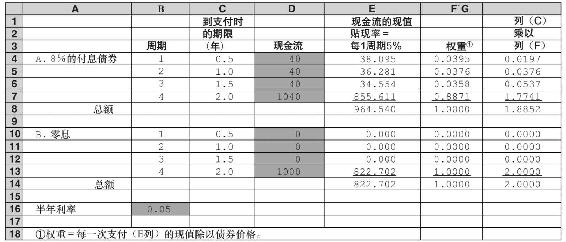
G欄的數字是支付期限和支付權重的乘積。每個乘積都是式(16-1)中相應的一項。根據公式,我們可以把G欄的數字相加計算出每一債券的久期。
零息債券的久期正好等於到期時間,即2年。這很好理解,因為僅有一次支付,而支付的平均期限必須是債券的期限。相比較,2年期債券的久期稍短一些,為1.8852年。
表16-4用來說明生成表16-3中所有內容的公式。表的輸入(詳細說明債券支付的現金流)在B~D欄中給出。在E欄中,我們用假設的到期收益率來計算每次現金流的現值。在F欄中,我們求出式(16-1)中的權重。在G欄中,我們計算支付期限和支付權重的乘積。所有這些數據都對應式(16-1)的計算中所需的數據。在單元格G8和G14中所計算得到的總額就是每個債券的久期。利用數據表可以輕鬆回答諸如“如果……將會……”的問題,如概念檢查16-1中的問題。
概念檢查16-1
假設年利率(APR)下降至9%。那麼在表16-3中的兩種債券的價格和久期將會發生什麼變化?
表16-4 計算久期的電子數據表公式
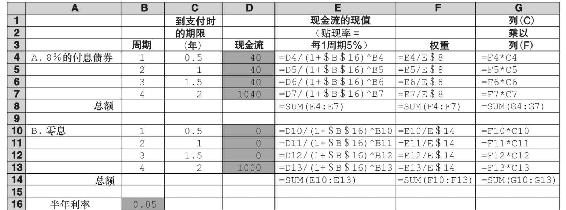
久期之所以是固定收益投資組合的關鍵概念至少有三個原因:首先,它是資產組合有效平均期限的簡單歸納統計;其次,它已經被證明是資產組合規避利率風險的一種基本工具,這些將在16.3節中探討;最後,久期是資產組合利率敏感性的一種測度,這是需要在此探討的內容。
我們已經知道債券價格的利率敏感性通常隨著其債券期限的增加而增加。久期的測度能夠量化這種關係。具體而言,當利率變化時,債券價格的變化率與其到期收益率的變化是相關的,可用公式表達如下:

債券價格的變化率等於債券久期乘以(1+債券收益率)的變化率。
實踐者運用式(16-2)時,在形式上略有不同。他們將修正久期(modified duration)定義為D*=D/(1+y),這裡Δ(1+y)=Δy,於是(16-2)改寫為:

債券價格的變化率正好是修正久期和債券到期收益率變化的乘積。因為債券價格的變化率與修正久期成比例,所以修正久期可以用來測度債券在利率變化時的風險敞口。實際上,下面可以看到,式(16-2)或等效的式(16-3),對於債券收益率的大幅度變化僅僅是近似有效的。只在考慮較小或局部的收益率變化時,這種近似才變得準確。
(注:對於債券收益變化,學習微積分的人會認識到修正久期和所得的債券價格成比例。對於收益的較小變化,式(16-3)可以重寫成:
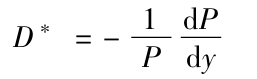
這樣,在現價的相鄰位置,它給出了債券價格曲線的斜率測度。實際上,式(16-3)可以根據y演化出以下的債券定價公式:
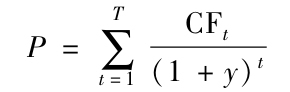
式中,CFt是在日期t支付給債券持有人的現金流。CFt代表到期日之前的利息支付。)
【例16-1】久期
表16-1中,考慮2年期、票面利率為8%且半年支付一次的債券,其出售價格為964.54美元,到期收益率為10%,該債券的久期是1.8852年。為進行比較,考慮以下零息債券,其期限和久期都是1.8852年。正如在表16-3中看到的,因為債券利息每半年償付一次,最好把半年定為一個週期。於是,每一債券的久期是1.8852×2=3.7704個(半年)週期,且每一週期的利率是5%。因此,每一債券的修正久期是3.7704/1.05=3.591個週期。
假定半年利率從5%上漲至5.01%。根據式(16-3),債券價格應該下降:
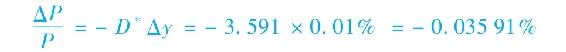
現在直接計算每一債券的價格變化。息票債券的初始銷售價格是964.540美元。當收益漲至5.01%時,價格下降到964.1942美元,下降了0.0359%。零息債券的初始賣價是1000/1.053.7704=831.9704美元。收益率更高時,它的賣價為1000/1.05013.7704=831.6717美元。價格下降了0.0359%。
結論是:相同久期的債券實際上利率敏感性相同,並且價格變化百分比(至少對於收益變化小的債券而言)等於修正久期乘以收益變化。
注:注意例16-1的另一層含義:我們從例子中可以看到當債券採取一年兩次付息時,將每次支付週期定為半年是很合適的。這也就說明我們可以將麥考利久期與(1+半年到期收益率)相除來修正久期的計算,這個除數通常又寫作(1+債券等值收益率/2),一般來講,如果一隻債券每年n次付息,修正久期與麥考利久期的關係可表示為D*=D/(1+yBEY/n)。
概念檢查16-2
a.在概念檢查16-1中,當市場利率為9%時,你計算了2年期、票面利率為8%且半年付息一次的債券的價格和久期。現在假定利率上升至9.05%,計算債券的新價值和價格變化百分比。
b.根據式(16-2)或者式(16-3)中的久期公式預測的債券價格,計算債券價格的變化百分比。將這個值與a中的答案進行比較。
16.1.3 什麼決定修正久期
我們在前面列出的馬爾基爾債券價格關係,給出了利率敏感性的決定因素。久期使我們能夠量化敏感性,例如,如果我們在利率上投機,久期將告訴我們這個賭注有多大。反之,如果我們想對利率保持“中性”,且僅與所選債券市場指數的利率敏感性相匹配,則通過久期我們可以測量這一敏感性,並在組合中模擬。正因為如此,瞭解久期的決定性因素至關重要。因此,在這一小節裡我們總結出幾項有關久期最重要特性的“法則”。債券價格對市場利率變化的敏感性受到三個方面因素的影響:到期時間、票面利率和到期收益率。
我們已經建立了如下法則:
久期法則1:零息債券的久期等於它的到期時間。
我們已經看到息票債券比相同期限零息債券的久期短,因為最後支付前的一切息票利息支付都將減少債券的加權平均時間。這說明了久期的另一個一般性質。
久期法則2:到期時間不變,當息票率較高時,債券久期較短。
這一性質與馬爾基爾的第五條關係相對應,它可歸因於早期息票支付對債券支付平均期限的影響。票面利率越高,早期支付權重也越高,且加權支付平均期限就越短。換言之,債券總值的較高部分與較早的利息支付密切相關,這種較早的利息支付對於收益率不太敏感。在圖16-2中,比較票面利率為3%和15%的債券久期圖,它們的收益率相同且都是15%。票面利率為15%的債券久期曲線位於票面利率為3%的債券相對應的久期曲線之下。
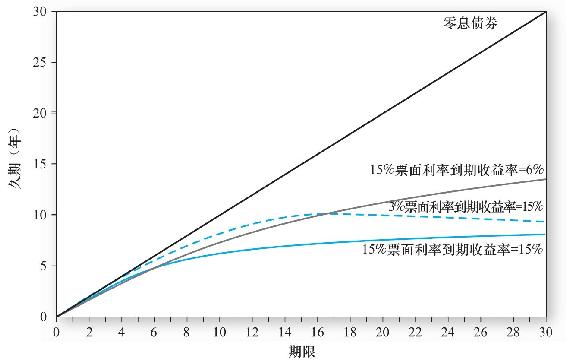
圖16-2 債券久期與債券期限
久期法則3:如果票面利率不變,債券久期通常會隨著期限增加而增加。債券以面值或者超出面值銷售,久期總是隨期限增加而增加。
久期的這一性質與馬爾凱的第三條關係相對應,非常直觀。奇怪的是久期不會總是隨期限增加而增加。對於貼現率很高的債券(見圖16-2中3%票面利率的債券),隨著期限增加,久期最終會下降。然而,事實上所有可以交易的債券都可以安全地假定久期隨到期時間的增加而增加。
注意在圖16-2中,零息債券的期限和久期是相同的。但是對於息票債券,到期時間增加一年時,它的久期增加卻少於一年。在圖中久期的斜率小於1.0。
雖然到期時間長的債券通常是長久期債券,但是久期可以更好地說明債券長期的性質,因為它還考慮了債券的支付情況。只有在債券不支付利息時,到期時間才是一個準確的數據,這時,期限和久期是相等的。
同時注意在圖16-2中,當它們以不同的到期收益率出售時,兩種利率為15%的債券有不同的久期。較低收益率的債券,久期更長。這是可以理解的,因為收益越低,債券支付期越遠,其現值就越大,而且它在債券總值中佔的比例也越大。於是,在加權平均計算久期的過程中,遠期支付的權重更大,導致測量出來的久期更高。這就確立了久期法則4。
久期法則4:保持其他因素都不變,當債券到期收益率較低時,息票債券的久期會較長。
我們上面已經提到,這個性質給人的直觀感受是,較高的收益率降低所有債券支付的現值,同時會較大幅度地降低遠期支付的價值。因此,在收益率較高時,債券總值的更多部分依賴於它的早期支付,這樣就降低了有限期限。法則4就是上述債券定價關係中的第六條,適用於息票債券。當然,對於零息債券,久期等於到期時間,與到期收益率無關。
最後,我們給出永久期限債券的久期公式。該公式源於式(16-1)給出的久期公式並與其一致,但是對於無數的現存債券而言,這一公式使用更為便捷。
久期法則5:終身年金的久期是:

例如,當收益率為10%時,每年支付100美元的終身年金的久期為1.10/0.10=11年,但是當收益率為8%時,久期為1.08/0.08=13.5年。
概念檢查16-3
利用法則4證明當利率降低時,終身年金債券的久期會增加。
式(16-4)表明,期限和久期的差別可以非常顯著。終身年金債券的到期時間是無限的,然而當收益為10%時,它的久期只有11年。年金早期現金流的現值加權對於久期的計算起決定性作用。
注意在圖16-2中,當到期時間變長時,收益率為15%的兩種息票債券的久期將收斂於有相同收益率的終身年金的久期,即7.67年。
息票債券的久期公式有點乏味,且像表16-3那樣的電子數據表用來修正不同期限和票面利率時會很麻煩。此外,它們假定債券處於利息支付週期開始的階段。幸運的是,電子數據表程序,如Excel,給出了處於利息支付期間的債券公式的概括。表16-5演示如何利用Excel計算久期。電子數據表使用很多慣例,如第14章中描述的債券定價電子數據表。
表16-5 運用Excel函數計算久期
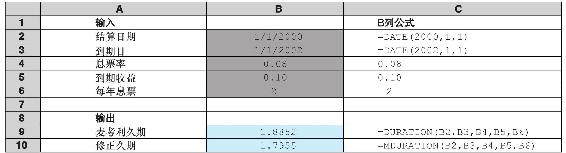
利用Excel日期函數DATE(year,month,day),在單元格B2和B3中輸入支付日期,例如今天的日期和到期日。在單元格B4和B5中以小數形式輸入票面利率和到期收益率。在單元格B6中,輸入每年的支付週期。單元格B9和B10中顯示麥考利久期和修正久期。該電子數據表表明,在表16-3中的債券久期確實是1.8852年。這隻兩年期債券並沒有確定的支付日期。我們將支付日期任意定為2000年1月1日,到期日正好是兩年後。
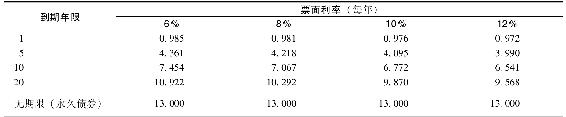
可交易債券的久期變化範圍很大。假定幾種債券為半年支付的息票債券且半年收益率為4%,表16-6給出了表16-5計算出的久期。注意久期隨著票面利率增加而變短,並一般隨到期時間增加而增大。根據表16-6和式(16-2),如果利率從8%上升至8.1%,票面利率為6%的20年期債券的價值會下降約10.922×0.1%/1.04=1.05%,然而票面利率為10%的1年期債券的價值僅僅下降0.976×0.1%/1.04=0.094%。[4]同時注意表16-6中,對於無期限債券而言,久期與票面利率無關。
表16-6 債券久期(到期收益率=8%APR;半年票面利率)
概念檢查16-4
利用表16-5來檢查前面陳述的一些久期法則。如果改變債券票面利率,久期會如何變化?同樣,如果改變到期收益率,久期會如何變化?如果改變期限,久期會如何變化?如果債券由每半年付息一次改為每年付息一次,久期將如何變化?為什麼憑直覺半年支付的債券久期更短?
[1] Burton G.Malkiel,“Expectations,Bond Price,and the Term Structure of Interest Rates,”Quarterly Journal of Economics 76(May 1962),pp.197-218.
[2] Sidney Homer and Martin L.Liebowitz,Inside the Yield Book:New Tools for Bond Market Strategy(Englewood Cliff,NJ:Prentice Hall,1972).
[3] Frederick Macaulay,Some Theoretical Problems Suggested by the Movements of Interest Rates,Bond Yields,and Stock Prices in the United States since 1856(New York:National Bureau of Economic Research,1938).
[4] 注意債券每半年付息一次,我們使用的是名義上的半年期到期收益率(即4%)來計算修正久期。