BUSINESS BOOKS

概念檢查答案

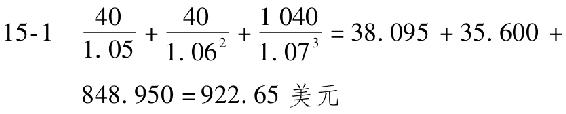
在這一價格水平上，到期收益率為6.945%［n=3；PV=（-）922.65；FV=1000；PMT=40］。該債券的到期收益率更接近3年期零息債券收益率而不是例15-1中票面利率為10%的附息債券的到期收益率。這種情況的意義在於：該債券票面利率低於例15-1中的債券，它的主要價值在第3年最後一次支付時才實現，所以它的收益率更接近3年期零息債券。

15-2　我們用類似例15-2中的方法比較兩種投資策略：

買入並持有4年期零息債券

=買入3年期零息債券，再投資於1年期債券

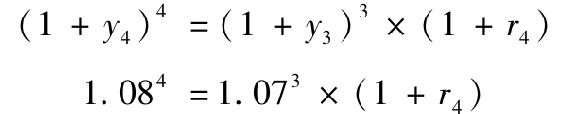
這意味著r₄=1.08⁴/1.07³-1=0.11056=11.056%。現在我們驗證4年期零息債券的收益率是後三年折現因子的幾何平均：

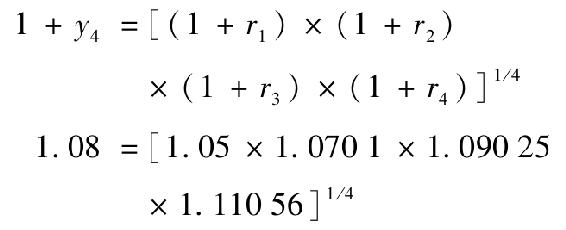
15-3　現在，3年期債券可以1000/1.07³=816.30美元的價格買入。明年，債券剩餘期限為2年。第2年短期利率為7.01%，第3年短期利率為9.025%。因此，根據下式，該債券明年的到期收益率與這些短期利率有關：

（1+y₂）²=1.0701×1.09025=1.1667

則它明年的價格為1000/（1+y₂）²=1000/1.1667=857.12美元。所以，1年期持有期收益率是（857.12-816.30）/816.30=0.05或者5%。

15-4　n年期即期利率是指剩餘期限為n年的零息債券的到期收益率。第n年的短期利率是指第n年將實行的1年期利率。最後，第n年的遠期利率是指能滿足“盈虧平衡條件”，使得兩種n年期的投資策略總收益相等的短期利率。第一種策略是投資n年期的零息債券，第二種策略是先投資n-1年期的零息債券，再投資1年期零息債券。即期利率和遠期利率當前可以得出，但由於利率的不確定性，未來短期利率不可預測。在未來利率確定的特殊情況下，從收益率曲線計算出的遠期利率應等於未來的實際短期利率。

15-5　7%-1%=6%。

15-6　風險溢價為0。

15-7　如果發行人更願意發行長期債券，則他們會願意接受比短期債券更高的預期利息成本。這種意願與投資者對長期債券的高利率要求相結合，形成了正的流動性溢價。

（此外，注意2年期零息債券的價格與3年期零息債券的價格之比為1+f₃=1.0903。）要構建一個組合貸款，買入一份2年期零息債券，同時賣出1.0903份3年期零息債券。初始現金流為0，在時刻2現金流為+1000美元，在時刻3現金流為-1090.30美元，這相當於在時刻2以9.03%的利率執行1年期遠期貸款的現金流。