e1 Zvi Bodie 投資學 v10
習題
基礎題
1.遠期利率與未來短期利率的市場預期之間的關係是什麼?解釋利率期限結構的預期和流動性偏好理論。
2.根據預期假說,如果收益率曲線是向上傾斜的,市場預計短期利率必然會上升。這句話是對、錯還是不確定?為什麼?
3.根據流動性偏好理論,如果預期通貨膨脹在以後幾年將會下降,長期利率將高於短期利率。這句話是對、錯還是不確定?為什麼?
4.如果流動性偏好假設是真的,當一段時期內的利率保持穩定,期限結構曲線的形狀將是怎樣的?
a.向上傾斜
b.向下傾斜
c.持平
5.根據純預期理論,下面有關遠期利率的哪一項是正確的?
a.僅代表預期的未來短期利率
b.對視市場預期的無偏估計
c.總是誇大未來短期利率
6.假設純預期利率是正確的,向上傾斜的收益率曲線表示:
a.利率在未來會上升
b.長期債券比短期債券風險大
c.利率在未來預期會下降
中級題
7.下表列出了不同期限的零息債券價格。計算每種債券的到期收益率並推導遠期利率。

8.假定預期假說是正確的,計算第7題中4年期債券隨時間推移的預期價格路徑,每年債券的收益率是多少?證明期望收益等於各年的遠期利率。
9.考慮下列面值為1000美元的零息債券:
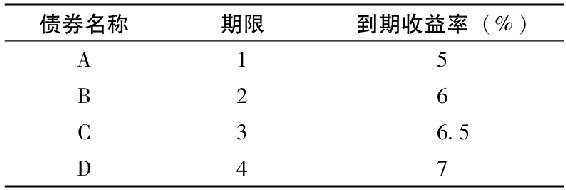
根據期望假說,預計從現在開始3年後的1年期利率是多少?
10.當前零息債券的期限結構是:

明年這個時候,你預期它是:

a.你預期下一年3年期的零息債券的收益率是多少?
b.根據預期理論,下一年市場預期的1年期和2年期零息債券的到期收益率是多少?市場預期的3年期債券收益率是高於還是低於你的預期?
11.當前,1年期零息債券的到期收益率為7%,2年期零息債券的到期收益率為8%。政府計劃發行2年期債券,每年付息,票面利率為9%。債券面值為100美元。
a.該債券售價多少?
b.該債券的到期收益率是多少?
c.如果收益率曲線的預期理論是正確的,則市場預期明年該債券的售價為多少?
d.如果你認為流動性偏好理論是正確的,且流動性溢價為1%,重新計算c。
12.下面列出了期限不同的零息債券價格。
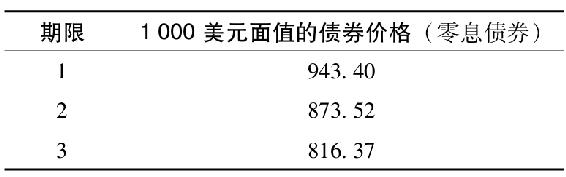
a.面值1000美元的債券,票面利率為8.5%,每年付息,3年後到期,該債券的到期收益率是多少?
b.如果第一年年底收益率曲線在8%處變成水平的,則持有該附息債券1年的持有期收益率是多少?
13.零息債券的價格反映的遠期利率如下:
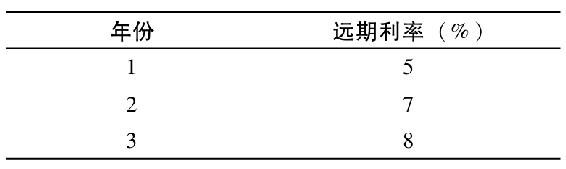
除零息債券外,投資者還可以購買一種每年付息60美元的3年期債券,面值為1000美元。
a.該付息債券的價格是多少?
b.該附息債券的到期收益率是多少?
c.根據預期假說,該附息債券的預期可實現的複合收益率是多少?
d.如果你預測一年後收益率曲線將在7%處變成水平狀,請預測持有該附息債券1年的期望收益率是多少。
14.觀察下列期限結構:

a.如果你相信明年的期限結構與現在相同,那麼,1年期零息債券和4年期零息債券哪個預期1年期收益率更高?
b.如果你相信期望假說,又會如何?
15.1年期零息債券的到期收益率為5%,2年期的是6%。票面利率是12%(每年付息)的2年期附息債券的到期收益率是5.8%。對投資銀行而言存在什麼套利機會?該套利行為的利潤是多少?
16.假設面值100美元的1年期零息債券現在售價為94.34美元,而2年期的零息債券的售價為84.99美元。你正在考慮購買2年期的每年付息債券,面值為100美元,年票面利率為12%。
a.2年期零息債券的到期收益率是多少?2年期附息債券呢?
b.第二年的遠期利率是多少?
c.如果期望假說可接受,第一年年底附息債券的期望價格是多少?附息債券第一年的預期持有期收益率是多少?
d.如果你接受流動性偏好假說,期望收益率是更高還是更低?
高級題
17.無違約風險的零息債券當前的收益率曲線如下表所示。

a.隱含的一年期遠期利率是多少?
b.假定期限結構的純預期假說是正確的。如果市場預期準確,明年的純收益曲線(即1年期與2年期零息債券的到期收益率)是多少?
c.如果你現在購買2年期零息債券,明年的總期望收益率是多少?如果你購買的是3年期零息債券呢(提示:計算當期價格和預期未來價格)?不考慮稅收。
d.票面利率為12%且每年付息的3年期債券的當前價格應為多少?如果你以此價格買入,明年的總期望收益率是多少(利息加價格變動)?不考慮稅收。
18.假設不同期限的零息債券的價格如下表所示。債券面值為1000美元。
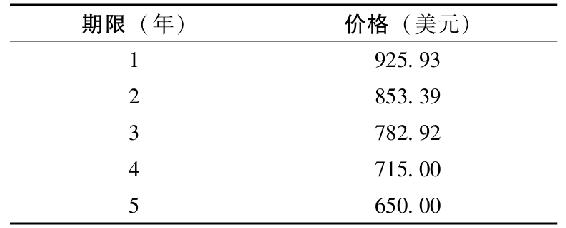
a.計算每年的遠期利率。
b.怎樣構建一個第3年開始執行的1年期遠期貸款?證實貸款利率等於遠期利率。
c.若遠期貸款從第4年開始執行,再次回答b中的問題。
19.繼續利用上題中的數據。假設你想構建一個三年後開始執行的2年期遠期貸款。
a.假設你於今日買入一份3年期零息債券。你需要賣出多少5年期零息債券才能使你的初始現金流為零?
b.這一策略中每年的現金流是多少?
c.對這筆3年後執行的2年期遠期貸款,實際的2年期利率是多少?
d.證實2年期貸款的實際利率是(1+f4)×(1+f5)-1。這樣,可以說明該2年期貸款利率就是這兩年中的遠期利率。或者,證明實際的2年期遠期利率等於