BUSINESS BOOKS

15.6　作為遠期合約的遠期利率

我們已經知道，利用式（15-5）可以從收益率曲線推導出遠期利率。通常，遠期利率不會等於最終實現的短期利率，甚至不會等於當前對短期利率的預期。但從某種意義上說，遠期利率是一種市場利率。假設你想現在為未來的某個時間安排一筆貸款，你今天就會對將要支付的利率達成協議，但貸款要到將來的某個時間才執行。這種“遠期貸款”利率怎樣確定呢？也許並不令人吃驚，下面所說的利率就是貸款期間內的遠期利率。我們舉例來說明這一點。

【例15-7】遠期利率合約

假設面值為1000美元的1年期零息債券的價格是952.38美元，面值為1000美元的2年期零息債券的價格是890美元。可見，1年期債券的到期收益率是5%，2年期債券的到期收益率是6%。第二年的遠期利率如下：

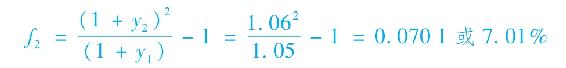
現在考慮下表中列出的策略。第一欄列出了本例的數據，第二欄推廣到一般情況。我們用B₀（T）表示T時刻到期的零息債券的當期價格。

初始現金流（0時刻）為0。你買入1年期零息債券支付952.38美元，即一般情況下的B₀（1），同時賣出每份2年期零息債券獲得890美元，即一般情況下的B₀（2）。若賣出1.0701份這樣的債券，初始現金流為0。^[1]

在時刻1，1年期債券到期，你獲得1000美元。在時刻2，你賣出的2年期零息債券到期，必須支付1.0701×1000=1070.10美元。你的現金流如圖15-7a所示。注意，你已經構建了一個“組合”遠期貸款：相當於1年後借入1000美元，過了一年後償還1070.10美元。因此這一遠期貸款利率為7.01%，恰好等於第二年的遠期利率。

通常，要構造這個組合遠期貸款，每買入一份1年期零息債券就要賣出（1+f₂）份2年期零息債券。這使得你的初始現金流為0，因為1年期和2年期零息債券的價格相差一個係數（1+f₂）。注意到：

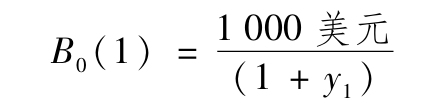
概念檢查15-9

假設3年期零息債券的價格是816.30美元。第三年的遠期利率是多少？怎樣構造一個組合的1年期遠期貸款，使得在t=2時執行，t=3時到期？

同時

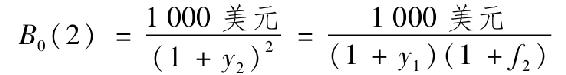
所以，當你賣出（1+f₂）份2年期零息債券後，你正好獲得買入1份1年期零息債券的足額現金。兩種零息債券到期時的面值都是1000美元，因此，時刻1與時刻2的現金流相差同樣一個係數，即1+f₂，如圖15-7b所示。可見，f₂就是遠期貸款的利率。

圖15-7　構建一個遠期貸款組合

顯然，還可以構造到期時間超過兩年的遠期貸款，也可以構造不同時期的貸款。本章末習題中的第18和19題可以引導你瞭解這些不同情況。

[1] 當然，現實中不可能賣出非整數份債券，但可以這樣考慮此部分交易。如果你賣出一份這種債券，相當於借入890美元，期限為2年。賣出1.0701份這種債券意味著借入890×1.0701=952.38（美元）。