e1 Zvi Bodie 投資學 v10
15.5 期限結構的解釋
如果收益率曲線反映未來短期利率的期望值,則它為固定收益投資者提供了一個潛在的有力分析工具。一旦利用期限結構推導出經濟體中其他投資者的利率期望,就可以把那些期望值作為分析的基準。例如,假設我們對利率將要下降的看法比其他投資者相對樂觀一些,我們將更願意在投資組合中加入長期債券。因此,在這一節,我們將深入研究通過詳細分析期限結構可獲得的信息。遺憾的是,當收益率曲線確實能夠反映未來利率的期望時,它也會反映其他一些因素,如流動性溢價。而且,利率變化預測可能具有不同的投資含義,這取決於這些變化是由預期通貨膨脹率的變化引起的還是由預期真實利率的變化引起的,而這又為合理地說明期限結構增加了新的複雜性。
我們已經知道,在確定性條件下,1加上零息債券的到期收益率簡單等同於1加上債券存續期內實際的短期利率的幾何平均值。這就是式(15-1)的含義,這裡給出它的一般形式:
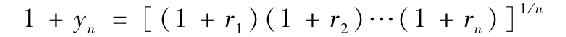
當未來利率不確定時,用遠期利率替代式(15-1)中的未來短期利率,得到:
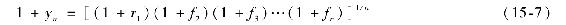
因此,不同期限債券的收益率與遠期利率之間存在直接關係。
首先,我們要弄明白什麼因素能夠解釋一條上升的收益率曲線。從數學上看,如果收益率曲線是上升的,fn+1一定高於yn。也就是說,在任一到期日n,由於下一期的遠期利率比到期收益率高,因此收益率曲線是向上傾斜的。這一規律是根據到期收益率是遠期利率的平均值(儘管是幾何平均值)得出的。
如果收益率曲線隨著期限增加而上升,就必然會出現到期日越長,“新的”遠期利率高於此前觀測到的遠期利率平均值的情況。這類似於,如果一個新同學的考試分數提高了全班的平均分數,則該同學的分數一定超過不包括她時全班的平均分數。要提高到期收益率,在計算平均值時就得增加一個高於原平均值的遠期利率。
【例15-6】遠期利率和收益率曲線的斜率
如果3年期零息債券的到期收益率是7%,則4年期債券的收益率滿足下式:
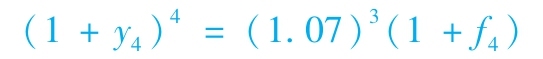
如果f4=0.07,那麼y4也等於0.07(確認這一點)。如果f4大於7%,y4將超過7%,收益率曲線將向上傾斜。例如,若f4=0.08,則(1+y4)4=(1.07)3×(1.08)=1.3230,y4=0.0725。
概念檢查15-8
參見表15-1,證明當且僅當第四期的遠期利率大於3年期債券的到期收益率y3,即大於7%時,y4將超過y3。
假定向上傾斜的收益率曲線總是與高於即期或當前到期收益率的遠期利率相關,那麼,下一步要弄清楚的是什麼原因引起更高的遠期利率。遺憾的是,對這個問題總有兩種可能的答案。我們說過,根據下式,遠期利率可能與預期的未來短期利率相關:
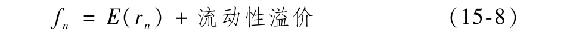
式中,流動性溢價可能是誘使投資者持有與其投資偏好不同的期限債券的必要條件。
順便指出,儘管流動性溢價假說的支持者一般認為流動性溢價為正,但它不一定是正的。如前文所說,如果大多數投資者傾向於長期投資,流動性溢價就可能為負。
在任何情況下,式(15-8)都表明有兩個原因可使遠期利率升高:一是投資者預期利率上升,這意味著E(rn)上升;二是者投資者對持有長期債券要求一個很高的溢價。儘管我們試圖從上升的收益率曲線中推導出投資者相信利率最終會上升,但這並不是一個有效推理。實際上,圖15-4a對這一推理提出了一個簡單的反例。圖中短期利率被預期永遠保持在5%,且流動性溢價也保持在不變的1%,因此,所有的遠期利率都是6%。結果顯示收益率曲線不斷上升,從一年期債券5%的收益率開始,隨著越來越多6%的遠期利率加入到期收益率的平均值中,長期債券到期收益率最終也將接近6%的平均水平。
因此,雖然未來利率將會上升的預期確實會導致收益率曲線上升,但反過來並不成立:上升的收益率曲線本身並不意味著更高的未來收益率預期。可能存在的流動性溢價所產生的影響使得任何試圖簡單地從期限結構中抽象出預期值的嘗試無法實行。但預計市場預期是一項重要工作,因為只有把自己的預期與市場價格所反映的預期相對比,我們才能知道自己對利率的看法是相對樂觀還是相對悲觀。
一個得出未來預期即期利率的辦法是假定流動性溢價不變。從遠期利率中減去這一溢價估值就得到市場預期利率。例如,再利用圖15-4中的例子,研究者從歷史數據估算出該經濟體中典型的流動性溢價為1%。從收益率曲線計算出遠期利率為6%,則未來即期利率的期望值是5%。
有兩個原因使得這一方法難以推廣。第一,幾乎不可能獲得準確的流動性溢價估計值。通常的估計方法是將遠期利率與最終實現的未來短期利率進行比較,計算兩者的平均差。然而,這兩個值的偏差有可能太大,而且由於影響實際短期利率的經濟事件難以預測,這種偏差也難以預測。因此,數據包含太多的噪聲,以至於不能得到期望溢價的可靠估計。第二,沒有理由相信流動性溢價是不變的。圖15-5顯示了自1971年以來長期國債價格收益率的波動情況。在此期間,利率風險波動劇烈,所以,我們應該預期不同期限債券的風險溢價是波動的,而且經驗證據表明,流動性溢價事實上是隨時間波動的。
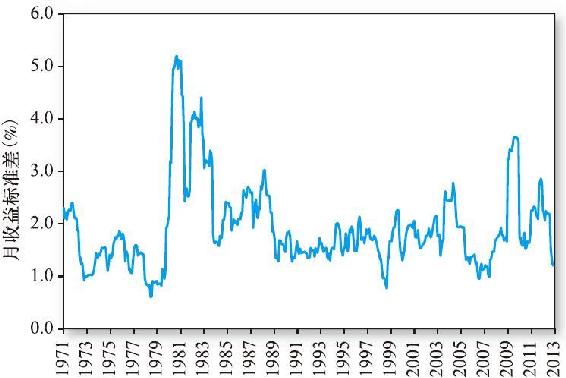
圖15-5 長期國債的價格波動
但是,非常陡的收益率曲線被許多專家解釋為利率即將上升的警示信號。實際上,收益率曲線是整個經濟週期的一個很好的指示器,因為當存在經濟擴張預期時,長期利率趨於上升。
我們通常觀察到的向上傾斜的收益率曲線是流動性溢價學說的經驗基礎,特別是在期限較短時更是如此,這一學說認為長期債券產生正的流動性溢價。由於收益率曲線經常因風險溢價而向上傾斜,這使得一條向下傾斜的收益率曲線就成為收益可能減少的強有力的證據。反過來,利率下降的預測又往往解釋為經濟衰退即將到來的信號。在自1970年起的七次經濟衰退中,每一次的短期利率都會超過長期利率。正因如此,收益率曲線的斜率能夠成為經濟領先指標的主要組成部分也就並不奇怪了。
圖15-6描述了90天短期國庫券和10年期國債的歷史收益率。長期債券的收益率通常超過短期債券的收益率,這意味著收益率曲線一般會向上傾斜。而且,該規則的例外似乎確實發生在短期利率下降之前,如果這個下降可以預知,將會導致收益率曲線向下傾斜。例如,圖15-6中1980~1981年,90天的收益率超過了長期收益率。這兩年就位於利率總水平猛烈下降和經濟急劇衰退之前。
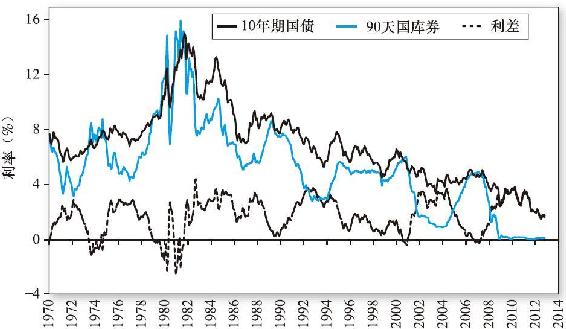
圖15-6 10年期和90天短期國庫券收益率:期限利差
為什麼利率會下降呢?這要考慮兩個因素:實際利率與通貨膨脹溢價。回想一下,名義利率是由實際利率與通貨膨脹補償因素構成的:
1+名義利率=(1+實際利率)(1+通貨膨脹率)
近似於:
名義利率≈實際利率+通貨膨脹率
因此預期通貨膨脹率和實際利率的變化都會引起預期利率的變化。通常,區分這兩種可能原因是很重要的,因為與它們相聯繫的經濟環境會有本質的不同。高實際利率可能意味著經濟的快速擴張、高政府預算赤字和緊縮的貨幣政策。儘管高通貨膨脹率可能源於經濟的快速擴張,但通貨膨脹也可能產生於貨幣供給的快速增長或供給方面對經濟的衝擊,如石油供給的中斷。
這些因素對投資的意義有很大區別。即使已經通過分析收益率曲線得出利率將要下降的結論,我們仍需要分析導致利率下降的宏觀經濟因素。