BUSINESS BOOKS

15.4　期限結構理論

15.4.1　期望假說

期限結構理論的簡單版本即期望假說（expectations hypothesis）。關於假說的共同看法是遠期利率等於未來短期利率的期望值，即f₂=E（r₂），並且流動性溢價為0。如果f₂=E（r₂）則長期收益等於未來期望收益率。另外，可以用從收益率曲線中得到的遠期利率推斷未來短期利率的市場預期。例如，式（15-5）中（1+y₂）²=（1+r₁）（1+f₂），如果期望假說是正確的，可以寫成（1+y₂）²=（1+r₁）［1+E（r₂）］。到期收益率也可以僅由當期和預期的未來單期利率決定。一個向上的收益率曲線是投資者期望利率上升的最好證據。

同時，當運用期望假說的時候，並不需要侷限於名義債券。華爾街實戰15-1指出，我們可以將這一理論運用到實際利率的期限結構中，並順便學習一些有關通貨膨脹率的市場預期的知識。

概念檢查15-6

如果期望假說是有效的，投資者持有與其投資觀點不同的期限的債券，我們可以得出哪些必要的溢價條件？

華爾街實戰15-1　期望假說與遠期通貨膨脹率

普通債券的遠期利率是名義利率。但是通過價格水平指數債券，例如通貨膨脹保護債券，我們可以計算遠期實際利率。由於名義利率和實際利率之間的差異近似等於預期通貨膨脹率，因此，比較名義和實際的遠期利率能讓我們對市場預期的未來通貨膨脹率有大致的概念。名義和實際之間的差值是一種遠期的通貨膨脹率。

作為貨幣政策的一部分，美聯儲委員為刺激經濟，會定期降低其聯邦基金利率。下面這張圖是在美聯儲宣佈這一政策的當天，從彭博截屏的5年期遠期名義利率和遠期實際利率的實時每分鐘利差。在宣佈當時，利差立即擴大，表明市場預期更加擴張性的貨幣政策最終會導致更高的通貨膨脹率。此圖中顯示的通貨膨脹率的上升非常溫和，從2.53%到2.58%，僅有0.05%，但是這項聲明的影響非常明顯，對於聲明市場調整的速度也令人驚歎。

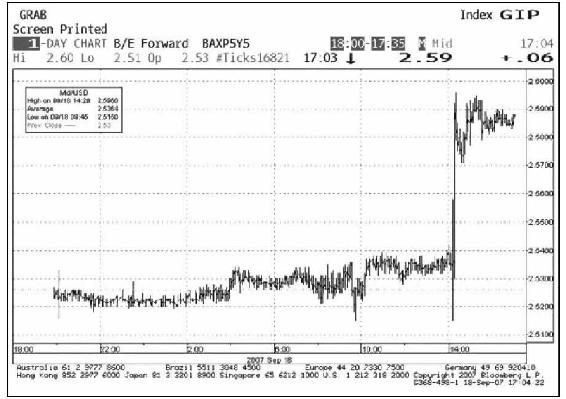
15.4.2　流動性偏好

我們曾經提到，除非遠期利率超過預期短期利率，即f₂>E（r₂），短期投資者不會持有長期債券。而長期投資者除非E（r₂）>f₂，否則也不會願意持有短期債券。換句話說，需要有溢價存在使兩種類型的投資者持有不同於他們投資理念的期限的債券。期限結構的流動性偏好理論的倡導者相信短期投資者佔據市場統治地位，所以遠期利率將會超過短期期望利率。f₂大於E（r₂）的部分（即流動性溢價）為正。

概念檢查15-7

流動性溢價假說也認為債券持有人偏好發行長期債券來鎖定借款費用。這種偏好將會對一個正的流動性溢價產生怎樣的影響？

為了更好地說明這些理論的不同內涵對利率期限結構的解釋，假定短期利率一直不變。假定r₁=5%，E（r₂）=5%，E（r₃）=5%等。在期望假說理論下，2年期到期收益率假說可以從下式得出：

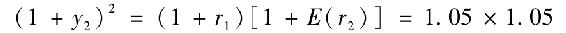
所以y₂=5%，相似地，所有期限債券的收益率均為5%。

相反，在流動性偏好理論下，f₂>E（r₂）。為了解釋這一點，假定流動性溢價為1%，因此f₂=6%。那麼，2年期債券：

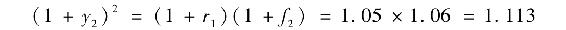
這意味著1+y₂=1.055。相似地，如果f₃=6%，那麼3年期債券的收益率可以由以下式子計算得出：（1+y₃）³=（1+r₁）（1+f₂）（1+f₃）=1.05×1.06×1.06=1.17978。

這意味著1+y₃=1.0567。這種情形的收益率曲線如圖15-4a所示。這類上升的曲線在實際中非常普遍。

如果利率隨著時間變化，那麼流動性溢價可能會阻礙由期望即期利率得出遠期利率。那麼每一期限的到期收益率是單期遠期利率的平均值。關於利率上升或下降的多種可能性可以在圖15-4中見到，如圖15-4b~圖15-4d所示。

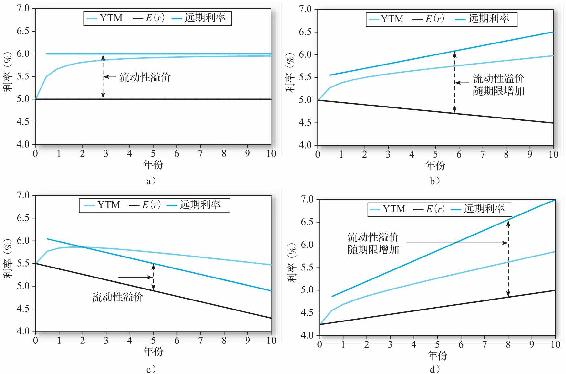
圖15-4　收益率曲線

注：a組：短期期望利率恆定，流動性溢價增長1%，收益率曲線上升；b組：短期期望利率下降，流動性溢價增長，收益率曲線上升；c組：短期期望利率下降，流動性溢價恆定，收益率曲線呈波狀；d組：短期期望利率上升，流動性溢價上升，收益率曲線驟然升高。