BUSINESS BOOKS

15.2　收益曲線與遠期利率

我們已經說明什麼是收益率曲線，但是沒有詳細說明它的來源。例如，為什麼收益率曲線有時向上傾斜，有時向下傾斜？利率期望值的發展怎樣影響今天的收益率曲線的形狀？

這些問題的答案並不簡單，所以我們將從一個已經公認的理想化的框架開始，然後再展開更符合實際情況的討論。首先，我們考慮一個確定性的場景，尤其是在一個所有的投資者都已經知道未來利率軌跡的情況下。

15.2.1　確定的收益率曲線

如果利率是確定的，我們怎麼看待表15-1中2年期零息債券的收益率要大於1年期零息債券收益率？期望一隻債券能提供更高的收益率是不可能的。在一個確定的沒有風險的世界中這是不可能發生的事情，所有的債券（實際上是所有的證券）必須提供相同的收益，否則投資者會競相購買那些高收益的債券直至它們的收益不再高於其他債券。

相反，上升收益率曲線顯示短期利率明年將會比現在更高。為了瞭解原因，來看看兩個2年期債券的投資策略。第一個策略是購買2年期到期收益率為6%的零息債券，持有至到期日。零息債券票面為1000美元，折算到今天的購買價為1000/1.06²=890美元，到期價格為1000美元。因此兩年的投資增長率為1000/890=1.06²=1.1236。

現在來看看另一個2年期策略，投資相同的890美元在1年期零息債券，其到期收益率為5%。當債券到期時，重新進行另一次1年期債券投資。圖15-2列出了這兩種策略的情況。下一年1年期債券的利率用r₂表示。

記住，在兩者都不包含風險的情況下，兩個策略必須提供相同的收益。因此，2年後兩策略的收益必須相等：

購買和持有2年期零息債券=循環投資1年期零息債券

即

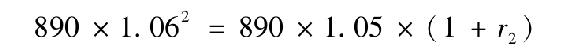
通過計算1+r₂=1.06²/1.05=1.0701，或者r₂=7.01%來得出下一年的利率。所以當1年期債券提供的到期收益率低於2年期債券時（5%相對於6%），我們將看到它具有補償優勢：它允許你下一年重新將你的資金投入到另一種也許會有更高收益率的短期國庫券中。相比於當年滾動購買1年期債券與一次性購買2年期債券吸引力相同的情形，下一年的收益率將會更高。

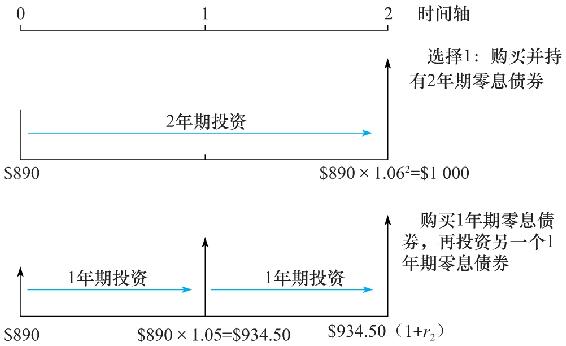
圖15-2　兩個2年期投資計劃

為了辨別將來可能會用到的長期債券的收益率和短期利率的區別，從業人員將會使用以下術語。他們把零息債券到期收益率叫作即期利率（spot rate），意思是對應於零息債券在今天持續了一段時間的利率。相反，既定區間內（例如一年）的短期利率（short rate）是在那一區間內的不同時間點均適用的利率。在我們的例子中，今天的短期利率是5%，下一年的短期利率是7.01%。

毫不奇怪，2年即期利率是當年的短期利率和下一年短期利率的平均值。^[1]但是因為複利的影響，平均是一個幾何學問題。我們再次通過使得這兩種2年期策略總收益相等的等式來了解這個問題：

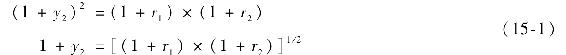
式（15-1）告訴我們為什麼收益曲線在不同時期內有不同的形狀。當下一年的短期利率r₂大於這一年的短期利率r₁時，兩個利率的平均值將會大於目前的利率，所以y₂>y₁，收益率曲線向上傾斜。如果下一年的短期利率比今年r₁要低，收益曲線是向下傾斜的。因此，收益曲線至少部分反映了對未來市場利率的預計。下面的例子用類似的分析方法得出了第三年的短期利率。

【例15-2】找出未來短期利率

現在來比較兩個3年期策略。一種是購買3年期零息債券，到期收益率如表15-1所示為7%，持有至到期。另一種是購買兩年期零息債券，到期收益率為6%，在第三年的時候購買1年期零息債券，短期利率為r₃，那麼投資基金在每種投資策略下的增長率將是：

購買並持有3年期零息債券=購買2年期零息債券，然後再購買1年期債券

即

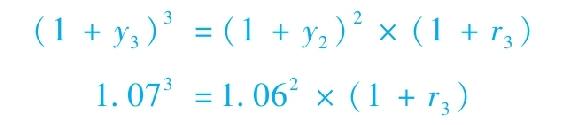
這就意味著r₃=1.07³/1.06²-1=0.09025=9.025%。另外，注意到3年期的債券反映了接下來3年折現因子的幾何平均：

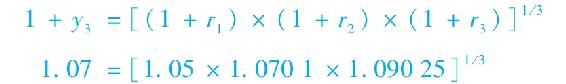
我們得出結論：長期債券的收益率或即期利率反映了在存續期內受市場預期影響的短期債券利率的軌跡。

圖15-3總結了我們分析的結果並強調短期利率與即期利率之間的區別。最頂端的線代表了每年的短期收益率。下面的線代表了從現在到每個相關到期日的即期收益率（或等同地，不同持有期限的零息債券的到期收益率）。

概念檢查15-2

用表15-1找出第四年的短期利率。證明4年期零息債券的折現因子是1加上接下來四年的短期利率的幾何平均數。

15.2.2　持有期收益率

我們曾經討論過我們所對比的債券的多年累積收益率應相等。在短期如1年的期限，持有期收益率又是怎樣呢？你可能認為債券以更高的到期收益率售出將會獲得更高的年化收益率，但是事實並不是這樣。實際上，一旦你不再這樣想，你將會很清楚這不可能是真的。在確定性的世界裡，所有的債券都必須提供相同的收益，否則投資者將會競相購買收益率更高的證券，推高價格，減少收益。這一過程可以用表15-1來解釋。

【例15-3】持有期收益和零息債券

如表15-1所示的1年期債券目前可以1000/1.05=952.38美元的價格買到，在1年內將達到面值。它不支付利息，所以總投資收益是價格升水，其收益率為（1000-952.38）/952.38=0.05。2年期的債券的買價可以是1000/1.06²=890美元。第二年債券的剩餘期限為1年，且1年的收益率為7.01%。因此，它下一年的價格為1000/1.0701=934.49美元，一年期持有期收益率為（934.49-890.00）/890.00=0.05，與5%的收益率相同。

概念檢查15-3

證明例15-1中的3年期零息債券收益率也是5%。提示：下一年，債券的剩餘期限是2年。使用圖15-3中的短期收益率計算從現在起下一年的2年期即期利率。

圖15-3　與即期利率相比的短期利率

15.2.3　遠期利率

下面的等式概括了從零息債券收益率曲線中推算出未來的短期收益率的方法。使得兩種n年期投資策略的總收益相等：買入並持有一隻n年期零息債券相等於買入（n-1）年零息債券再將收益投入一隻1年期債券。

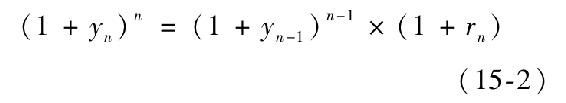
式中，n指的是期數，y_n為n期零息債券在第n期的到期收益率。根據觀察到的收益率曲線，用式（15-2）可以解出最後期的短期利率：

式（15-3）有一個簡單的解釋。等式右邊分子的含義是n期零息債券持有至到期的投資總增長係數，同理，分母的含義是n-1期投資的總增長。由於前者比後者的投資期限多一年，其增長量的差別一定是將n-1年的回報再投資一年n。

當然，當未來利率不確定時，如現實中的那樣，無法推斷未來“確定”的短期利率。今天無人得知將來的利率是什麼，最多就是能推測預期值並考慮到不確定性。但是人們仍然普遍通過式（15-3）來推斷未來利率收益率曲線的隱含意義。由於認識到未來利率的不確定性，我們將以這種方式推斷出來的利率稱為遠期利率而不是未來短期利率，因為它不必是未來某一期間內的實際利率。

如果n期的遠期利率為f_n，我們可用下式定義f_n：

經整理有：

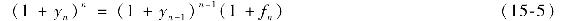
在這裡，遠期利率被定義為“損益平衡”的利率，它相當於一個n期零息債券的收益率等於（n-1）期零息債券在第n期再投資所得到的總收益率。如果第n期的短期利率等於f_n，兩種n年期投資策略的總收益將會是相等的。

【例15-4】遠期利率

假定債券交易員使用表15-1中的數據。4年期遠期利率可以由下式計算：

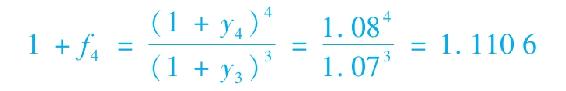
因此，遠期利率是f₄=0.1106或者11.06%。

概念檢查15-4

你已經在前面的內容中知道了許多種“利率”。解釋即期利率、短期利率與遠期利率之間的差別。

我們再次強調未來的實際利率並不一定與從今天的數據計算得出的遠期利率相等。實際上，預期的未來短期利率在實際中也不一定與遠期利率相等。這個問題我們會在第16章中強調。現在，我們將要指出遠期利率與未來短期利率在特殊的利率確定的情況下是相等的。

Excel應用：即期和遠期收益

下面的電子數據表（www.mhhe.com/bkm）的數據可用於預測價格和附息債券的收益率，以此來計算一年期和多年期的遠期利率。即期收益來源於以面值出售的債券的收益率曲線，也指當前利息或未到期債券的收益率曲線。

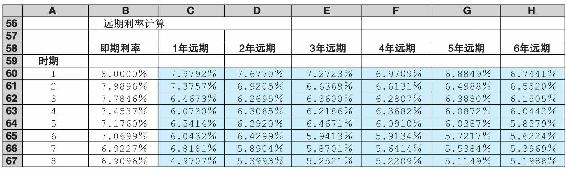
每個期限的即期利率用於計算每一時期現金流的現值。這些現金流的總額是這些債券的價格。根據這一價格，就可以計算出債券的到期收益率。如果錯誤使用了未到期債券的到期收益率來為債券的利息收益折現，就會得出一個完全不同的價格。差異在數據表中計算出來了。

[1] 在算術平方根上，加上n個數被n整除。在幾何平均上，將n個數相乘，再開n次方。