e1 Zvi Bodie 投資學 v10
14.3 債券收益率
大部分的債券都不按照面值進行出售,但是除非有違約情形,基本上都會以面值進行到期支付。我們希望有一種指標,既可以解釋當前收入,又可以說明債券在整個存續期內的價格漲跌。到期收益率是總收益率的標準度量。當然,它並非完美,下面將討論該度量指標的幾種變化形式。
14.3.1 到期收益率
現實中,考慮購買債券的投資者並不是根據承諾回報率來考慮是否購買債券。相反,是通過債券價格、到期日、票息來推斷債券在其存續期內的收益。到期收益率(yield to maturity,YTM)被定義為債券的支付現值與其價格相等的利率。該利率通常被視為在購買日至到期日之間持有債券所獲得的平均收益率的測量。為了計算到期收益率,在給定債券價格的條件下,求解關於利率的債券價格方程。
【例14-4】到期收益率
假設一個票面利率為8%、期限為30年的債券的賣價為1276.76美元。在此價格上購買該債券的投資者獲得的平均回報率是多少?為回答這一問題,須找出使持有60期半年支付的現值與債券價格相等時的利率,是與被考察的債券價格相一致的利率。因此,在以下方程中求解利率r:
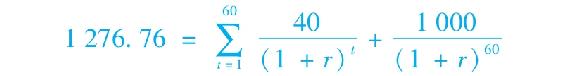
或等價於:
1276.76=40×年金因子(r,60)+1000×面值因子(r,60)
上述方程中僅有利率r一個未知變量。可以使用財務計算器或電子數據表來求得半年期利率r=0.03或3%,即該債券的到期收益率。[1]
財經版面報道的收益率是年化收益率,用簡單的單利方法即可將半年收益率轉化為年化收益率,得到年利率,即APR。用單利方法計算的收益率也被稱為“債券等值收益率”。因此,對半年收益率加倍,即可被報道為等值收益率為6%。然而,債券的實際年化收益率要考慮複利。如果一種債券每6個月的收益率為3%,那麼12個月後,1美元投資加利息的增長為1×(1.03)2=1.0609美元。債券的實際年利率是6.09%。
Excel也提供了到期收益率的函數,該函數對介於利息支付日之間的債券的計算很有用。該函數為:
=YIELD(結算日,到期日,年票面利率,債券價格,贖回價值相對面值的百分比,年付息次數)
在函數中使用的債券價格為淨價,不包含應計利息。例如,為獲得例14-4中債券的到期收益率,可以利用表14-3中的B列。如果利息是按年支付的,需要將記載條目中的年支付改為1(見單元格D8),收益率略微下降至5.99%。
表14-3 在Excel中求到期收益率
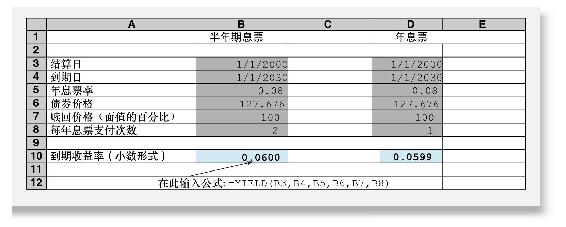
債券的到期收益率為債券投資的內部收益率。如果假設所有債券都能以此收益率投資,則到期收益率可以視為整個債券存續期內的複合收益率。[2]到期收益率被廣泛認為是平均收益的替代指標。
債券的到期收益率有別於當期收益率(current yield),當期收益率為債券的年利息支付除以債券價格。例如,票面利率為8%、30年期債券的當前售價是1276.76美元,則當期收益率為每年80/1276.76=0.0627或6.27%。相比較,債券的實際年到期收益率為6.09%。對超出面值溢價出售的債券而言(1276美元而不是1000美元),票面利率8%超過了當期收益率6.27%,當期收益率超過了到期收益率6.09%。票面利率之所以超過當期收益率,是因為票面利率等於利息支付除以面值(1000美元),而非債券價格1276美元。當期收益率超過到期收益率的原因則在於到期收益率包含了債券的潛在資本損失。現在以1276美元購買債券,到期日其價格將最終跌至1000美元。
例14-4說明了這樣一條規律:對溢價債券(premium bond)而言(債券以高於面值的價格出售),票面利率高於當期收益率,當期收益率高於到期收益率;對折價債券(discount bond)而言(債券以低於面值的價格出售),上述概念正好相反(見概念檢查14-3)。
通常會聽到人們談論債券收益。在這些情況下,大多指的是到期收益率。
概念檢查14-3
當債券以低於面值的折扣價出售時,票面利率、當前收益率、到期收益率三者是什麼關係?請用票面利率為8%(每半年支付一次),當前銷售該債券的到期收益率為10%為例說明。
14.3.2 贖回收益率
到期收益率假設債券是在持有至到期的情況下計算。然而,如果債券是可贖回的,或者在到期日之前終止,該如何度量贖回條款下債券的平均回報率呢?
圖14-4說明了可贖回債券持有者的風險。圖中上方曲線表示面值1000美元、票面利率8%、期限30年的“普通”債券(即不可贖回債券)在不同市場利率條件下的現值。如果利率下降,與承諾支付的現值相等的債券價格就會隨之上升。
現在考慮一種具有相同票面利率和到期日,但發行方可以按面值的110%,即1100美元贖回的債券。當利率下降時,發行方預定支付的現值將會上升。但由於贖回條款允許發行方以贖回價格贖回債券,因此若贖回價格低於預定支付的現值,發行方便可能會從債券持有者手中贖回債券。
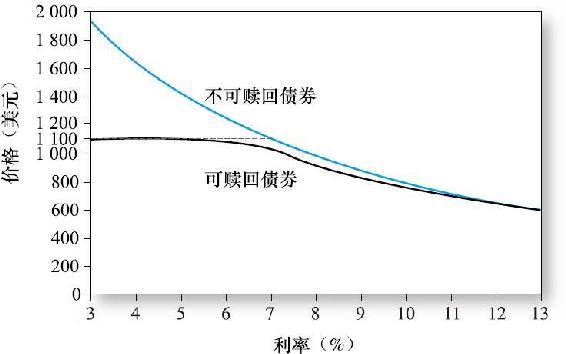
圖14-4 債券價格:可贖回債券與不可贖回債券
注:利率為8%,30年期,半年付息一次。
圖14-4中下方線條表示可贖回債券的價值,當利率較高時,因為預定支付的現值低於贖回價格,故贖回風險可忽略不計。因此,不可贖回債券與可贖回債券價值相互收斂。然而,在低利率條件下,兩種債券價格開始發散,其差異反映了能以贖回價格回購公司債券的期權價值。在利率很低的情況下,預定支付的現值超過了贖回價格,債券被贖回,該點的值就是贖回價格,即1100美元。
這一分析表明,如果債券極有可能被贖回,相對於到期收益率而言,債券市場分析師可能對贖回收益率更感興趣。贖回收益率的計算與到期收益率的計算基本相同,只是要以贖回日代替到期日,以贖回價格代替面值。這種計算方法有時被稱為“首次贖回收益率”,因為假設贖回發生在債券首次可贖回的時間。
【例14-5】贖回收益率
假設票面利率為8%、30年期的債券售價為1150美元,並且該債券可在10年後以1100美元贖回。使用下列輸入值可計算到期收益率和贖回收益率。

贖回收益率為6.64%[為了在計算器上驗證該結果,輸入n=20,PV=(-)1150,FV=1100,PMT=40,計算出收益率i為3.41%,或者6.82%的債券等價收益率]。在Excel中,可用以下命令計算贖回收益率:=YIELD(DATE(2000,01,01),DATE(2010,01,01),0.08,115,110,2)。值得注意的是,贖回價值輸入為110,即面值的110%。
我們注意到大多數可贖回債券在發行時都有一個最初的贖回保護期。此外,還存在隱含形式的贖回保護,即債券以贖回價為基礎進行高折價銷售。即使利率下降了一點,高折價的債券仍以低於贖回價格的價格出售,這樣也就不需要贖回了。
概念檢查14-4
a.兩種10年期債券的到期收益率目前均為7%,各自的贖回價格都是1100美元。其中一個票面利率為6%,另一個為8%。為簡便起見,假定在債券的剩餘支付現值超過贖回價格時立即贖回。如果市場利率突然降至6%,每種債券的資本利得分別是多少?
b.20年期、票面利率為9%的半年付息債券,5年後可贖回,贖回價格為1050美元,如果現在以8%的到期收益率賣出,則債券的贖回收益率是多少?
如果利率進一步降低,以接近贖回價格出售的溢價債券很容易被贖回。如果利率下降,一種可贖回的溢價債券所提供的收益率可能低於折價債券的收益率,因為後者潛在的價格上升不會受到贖回可能性的限制。相對於到期收益率而言,溢價債券的投資者通常對債券的贖回收益率更感興趣,因為債券在贖回日可能會被贖回。
14.3.3 已實現的複合收益率和到期收益率
如果所有債券都以與到期收益率相等的利率再投資,則到期收益率就將等於在整個存續期內所實現的收益率。例如,某兩年期債券以面值出售,每年付息一次,票面利率為10%。如果100美元的利息支付以10%的利率再投資,那麼投資於債券的1000美元兩年後將增長為1210美元,如圖14-5a所示。如果將第一年所支付的利息再投資,則第二年加上利息為110美元,再加上第二年利息支付以及面值償還,總額共計1210美元。
總而言之,投資的初值V0=1000美元,兩年後的終值V2=1210美元。因此,複合收益率可由以下方程計算:
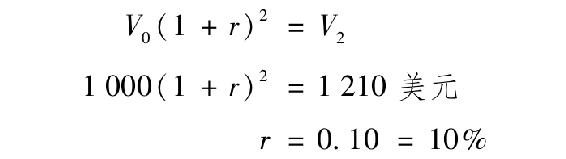
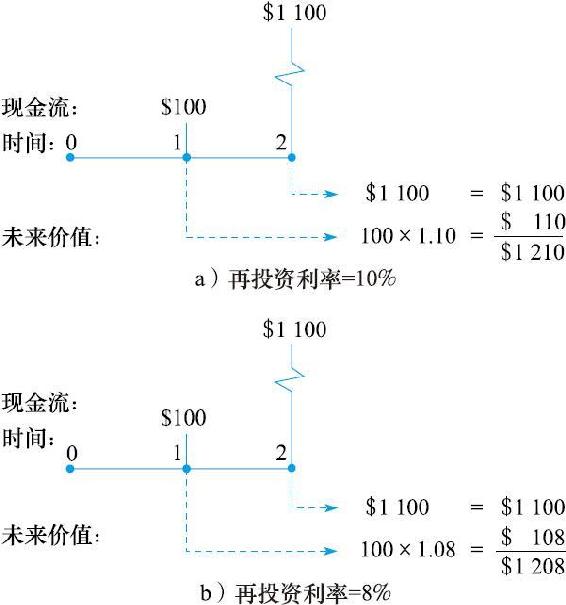
圖14-5 投資資金的增長
再投資利率等於到期收益率10%,已實現的複合收益率等於到期收益率。
如再投資利率不等於10%,會出現怎樣的情況呢?如果債券能以高於10%的利率再投資,資金增長將超過1210美元,同時實現的複合收益率也將超過10%。如果再投資利率低於10%,則實現複合收益率也會降低。考慮下面這個例子。
【例14-6】實現的複合收益率
如果首次利息支付再投資收益率不足10%,那麼該投資的終值將低於1210美元,同時實現的複合收益率也將低於10%。舉例說明,假設債券的投資利率僅為8%。計算見圖14-5b。
首次利息支付及其利息的未來價值為:100×1.08=108美元+兩年後的現金支付(第二年利息加面值)為:1100美元
=投資及利息再投資的總價值為:1208美元
假設所有利息支付都再投資,實現的複合收益率為全部投資金額的複合增長率。投資者以1000美元面值購入債券,該投資將增長至1208美元。
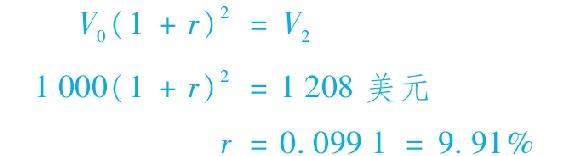
例14-6解決了當再投資利率隨時間變化時,常規到期收益率存在的問題。常規到期收益率將不再等於實現的複合收益率。然而,在未來利率不確定的情況下,期間利息再投資的利率也是未知的。因此,儘管在投資期結束後能夠推算出實現的複合收益率,但在無法預測未來再投資利率的情況下,並不能事先計算出來,這大大降低了實現的複合收益率的吸引力。
在各種持有期或投資水平下,預測實現的複合收益率被稱為水平分析(horizon analysis)。對總收益的預測,既依賴於持有期結束時賣出債券的價格,又依賴於利息再投資所能獲得的收益率。債券的賣出價格又依賴於持有期到期收益率。對於較長的投資期限,利息再投資佔了最終收益的較大部分。
【例14-7】水平分析
假設以980美元的價格購買一隻30年期、票面利率為7.5%(按年度支付)的債券(其到期收益率為7.67%),並計劃持有20年。當出售該債券時,預計到期收益率為8%,利息再投資收益率為6%。在投資期限結束時,該債券剩餘期限為10年,因此該債券的預計賣價為966.45美元(按照8%的到期收益率)。20年利息支付由於複利漲至2758.92美元(20年期利率為6%的75美元年金的終值)。
基於以上預測,980美元的投資在20年內將漲至:966.45+2758.92=3725.37美元,對應於6.90%的年複合收益率:
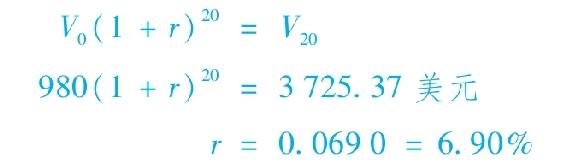
例14-6和例14-7證實了,隨著利率變化,債券投資者實際上受到兩類風險的影響。一方面,當利率上升時,債券價格下跌,這將降低資產組合的價值;另一方面,再投資利息收入在高利率下能取得更高的複利,而再投資利率風險(reinvestment rate risk)將對債券價格風險產生影響。在第16章中,我們將更詳細地探討折中問題,並且投資者通過仔細調整債券組合,在任何給定投資期限上都能精確地平衡這兩種影響。
[1] 在財務計算器中,進行如下輸入:n=60期,PV=-1276.76,FV=1000,PMT=40,就能計算出利率(COMP i或CPT i)。注意到所輸入的債券現值,或PV為-1000美元,這是因為大多數計算器將債券的初始購買價格視為現金流出。表14-3展示的就是如何用Excel求得到期收益率。如果沒有財務計算器或者電子數據表程序,要求解該方程,則需要採用試錯法。
[2] 如果再投資利率不等於債券的到期收益率,則複合收益率將不同於到期收益率,如例14-6和例14-7中所示。