BUSINESS BOOKS

14.2　債券定價

由於債券的面值和本金償還都發生在未來的數月或者數年後，投資者願意為這些收益權支付的價格取決於未來獲得的貨幣價值和現在所持有的現金價值的比較。這種現值計算取決於市場利率。正如第5章中所看到的，名義無風險利率等於實際無風險利率與補償預期通脹的超出實際利率的溢價之和。此外，由於大多數債券並不是無風險的，貼現率將會包含諸如違約風險、流動性、稅收屬性、贖回風險等債券具體特徵的溢價。

為簡化問題，假設只有一種利率適用於任意期限的現金流貼現，但可以放寬該假設。實際上，不同時期的現金流會有不同的貼現率，我們暫時忽略這一限制。

為了給證券定價，先用適當的貼現率對預期現金流貼現。債券的現金流包括到期日之前的利息收益和到期面值償還。因此：

債券價值=利息現值+面值現值

如果我們稱到期日為T，利率為r，債券價值可表示為：

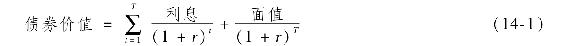
從式（14-1）中的累積求和公式可知，須把每期利息收益的現值相加，每次利息的貼現都是基於其支付的時間。式（14-1）等式右邊第一項是一個年金的現值，第二項是債券到期日支付面值的現值。

回顧金融學入門課程的內容，當利率為r時，存續期為T的1美元年金的現值是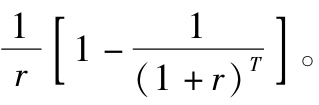

該式被稱為利率為r的T期年金因子。類似地，則可被稱為折現因子，即在T期時1美元的收益的現值。因此，債券的價格可表示為：

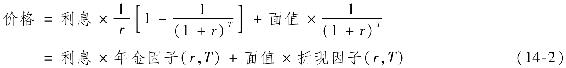
（注：以下是年金現值公式的簡便推導：期限為T的年金可視為等價於首次支付出現在當期末的永久年金減去首次支付出現在T+1期末的另一永久年金。當期永久年金與延期永久年金的差值正好為T期支付。由於每期支付為1美元的年金的價值是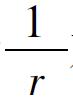，因此，延期永久年金的現值為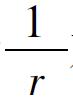對其餘T期的貼現，即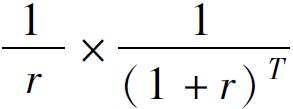。因此該年金的現值等於當其支付的永久年金減去延期永久年金的現值，即為）

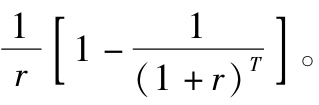【例14-2】債券定價

前面我們討論過這樣一隻債券，票面利率為8%，30年到期，面值為1000美元，每半年付息一次，每次40美元。假設年利率為8%，或每半年的利率為4%。債券的價值為：

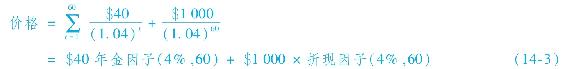
很容易得出該債券60次支付每次半年利息40美元的現值為904.94美元，以及最終支付的1000美元面值的現值95.06美元，債券的總價值為1000美元。該值可以通過式（14-2）直接計算，也可以使用財務計算器（見例14-3）、電子數據表（見Excel應用）或一套現值計算表計算獲得。

在此例中，票面利率等於市場利率，債券的價格等於面值。如果市場利率不等於債券票面利率，則債券不會以面值出售。例如，如果市場利率提高到10%（半年為5%），債券價格將下降189.29美元至810.71美元，計算如下：

40×年金因子（5%，60）+1000×折現因子（5%，60）=757.17+53.54=810.71（美元）

利率越高，債權人所獲收益的現值越低。因而，債券價格隨著市場利率的上升而下降。這是債券定價中一個極其重要的普遍規律^[1]。

債券價格的計算過程較為煩瑣，通過電子製表軟件或財務計算器可以將其簡化。財務計算器預先將現值與未來值程序化，這使得我們在解決諸如例14-2中的案例時遇到的排序計算問題得到極大的簡化。基本的財務計算器以五個按鍵對應諸如債券計價問題等貨幣時間價值問題的五個輸入要素：

1.n為時間週期的數量。就一筆債券而言，n等於截至票據到期日時間週期的數量。如果這筆債券為半年付息一次，n為半年期的數量或者說相當於半年一次的息票付款次數。例如，如果一筆債券還有10年到期，當支付週期為半年時，你需要在n的位置輸入20。

2.i為每個時間週期的利率，以百分比形式（而不是小數）表示。例如，如果利率是6%，你需要輸入6而不是0.06。

3.PV為現值。許多計算器要求以負數形式對PV進行錄入，用以強調購買購買債券為現金流出，而利息收入及票面價值為現金流入。

4.FV為債券的未來價值或面值。通常來講，FV被解釋為一次性支付的未來現金流，其中，對債券來講就是其面值。

5.PMT是每期付款額。對於有息債券來講，PMT就是付息金額；對於零息債券來講，PMT就是0。

以上五要素，給出任意四個將會自動計算出第五個。我們以例14-2中的債券為例進行說明。

【例14-3】以財務計算器進行債券定價

當市場年利率為8%時，想要得到債券價格，需要輸入以下內容（以任意順序）：

n　60　距離債券到期還剩30年，因此它需要進行60次每半年付息。

i　4　半年期的市場利率為4%。

FV　1000　當債券到期時將會一次性產生1000美元的資金流動。

PMT　40　每半年付息金額為40美元。

在大多數的計算器中，此時你需要按下“計算”鍵（標COMP或者CPT）並點擊PV即可得到債券價格，即債券現金流的現值。如果你按照上述進行操作，此時得到的值為-1000。負號表示雖然投資者通過債券獲得了資金流，但是買入債券的資金是一筆現金流出，或者說是一筆負現金流。如果你想要獲得在利率為10%時債券的價值（見例14-2第二部分），只需要將半年期利率5%輸入（輸入“5”並點擊“i”），此時再計算PV，你會得到PV=-810.71。

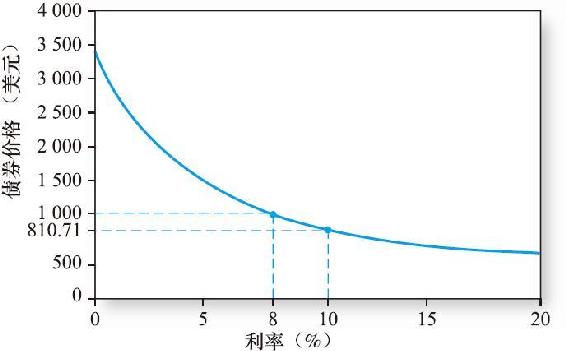
圖14-3　債券價格與收益率的反向關係

注：債券為30年期，利率為8%，半年付息一次。

圖14-3中反映了30年期、年利率為8%的債券價格與一定範圍內的利率水平之間的關係。其中，當利率為8%時，債券以面值出售；當利率為10%時，售價則為810.71美元。負斜率說明了債券價格與收益率之間的負相關關係。從圖14-3中曲線的形狀可以觀察到利率的上升導致的價格下跌的幅度要小於相同程度的利率下降導致的價格上升的幅度。債券價格的這一特性被稱為凸性（convexity），因為債券價格曲線的凸型形狀。凸性反映了隨著利率的逐漸上升，所引起的債券價格的下降幅度是逐步減小的。^[2]因此，價格曲線在較高利率時會變得平緩。我們將在第16章中再討論凸性問題。

公司債券一般以面值發行。這意味著公司債券發行的承銷商（即為發行人向公眾銷售債券的公司）必須選擇與市場收益率極為接近的票面利率。在一級市場上，承銷商試圖將新發行債券直接銷售給客戶。如果票面利率不夠高，投資者將不會按面值購買債券。

概念檢查14-2

計算30年期限、票面利率為8%的債券在市場利率每半年為3%時的價格。比較利率下降時的資本利得和當利率上升5%時的資本損失。

債券發行之後，債權人將在二級市場買賣債券。在各類市場中，債券價格與市場利率呈反向變動。

收益率與價格的負相關關係是固定收益證券的核心特徵。在第16章中我們將深入討論債券價格對市場收益率的敏感性。現在只集中討論決定這種敏感性的關鍵因素，即債券的期限。

一般規則是：在假設其他因素相同的情況下，債券的期限越長，債券價格對於利率波動的敏感度越高。如表14-2給出了票面利率為8%的債券在不同市場收益率和不同期限下的價格。對於任何偏離8%的利率（債券以面值出售的利率），期限越長，價格波動越大。

表14-2　不同市場利率下的債券價格

這一點是有價值的。如果投資者在8%的票面利率購買了債券，而市場利率隨後上升，則投資者將承擔損失：在其他投資能獲得更高收益的情況下，投資者的資金僅能獲得8%的固定收益。這可以從債券的資本損失及債券價格下跌中得到反映。資金被套牢的時間越長，損失越大，相應的債券價格的下跌幅度越大。表14-2中，1年期債券的價格敏感度很小，也就是說，風險收益的期限僅為1年時，利率的變化並未構成太大的威脅。但是，對於30年期的債券，利率的波動對於債券的價格就會產生很大的衝擊。期限最長的債券，折現的作用最強。

這就是為什麼短期國債如國庫券被認為是最安全證券的原因。它們不僅沒有違約風險，而且很大程度上也沒有因利率波動引起的價格風險。

付息日之間的債券定價

債券定價式（14-2）假設下一次票息支付恰好為一個付息期。年度付息債券，間隔為一年；半年付息債券，間隔為半年。但如果想在一年365天，而不只是其中的一個或兩個付息日上對債券定價，該如何定價呢？

原則上，債券處於付息日之間並不會影響定價。定價的程序仍然相同：計算出待支付的收益的現值並加總。但如果是在付息日期間，在支付前將存在一個剩餘時間，這會使計算複雜化。

幸運的是，Excel及其他電子數據表程序中都包含債券定價功能。輸入今天的日期以及債券的到期日，電子數據表就可以提供任何時間的債券價格。

如我們之前指出的，債券的報價通常不包含應計利息。在財經版面出現的報價被稱為淨價。投資者購買債券支付的包含應計利息的價格被稱為全價。因而：

全價=淨價+利息

當一隻債券付息時，淨價等於全價，此時應計利息為0。然而這並不是定律，也有例外。

Excel的定價功能能夠計算債券的淨價。全價則需要用淨價加上支付利息才可獲得。幸運的是，Excel也提供了函數來計算最後付息日的天數，因此能用於計算應計利息。下面的Excel應用顯示瞭如何使用這些函數，且提供了操作實例，實例包括剛剛支付過利息因而應計利息為0的債券，以及在付息日之間的債券。

Excel應用：債券定價

Excel和大多數其他電子數據表程序都提供了用於計算債券價格和收益的內置函數。它們一般要求輸入購買債券的日期（稱為清算日）和債券的到期日。債券價格的Excel函數為：

=PRICE（清算日，到期日，年利率，到期收益率，贖回價值與票面價值的百分比，年付息次數）

對圖14-1中顯示的票面利率為2.25%、2018年7月到期的債券，在下列電子數據表中輸入這些數據（注意，在電子數據表中我們在輸入利率時要採用小數的形式而不是百分比），也可以在Excel中簡單地輸入函數：

=PRICE（DATE（2012，7，31），DATE（2018，7，31，），0.0225，0.0079，100，2）

Excel中用來計算結算和到期日的DATE函數的格式為DATA（年，月，日）。第一個日期（2012年7月31日）為債券購買日期，第二個日期（2018年7月31日）為債券到期日。大多數債券在15日或者最後一個工作日付息。

注意到票面利率和到期收益率都是用小數而非百分比的形式表示的。在大多數情況下，贖回價值為100（即面值的100%），其價格也類似地使用面值百分比來表示。偶爾也會遇到以面值的溢價或折價來進行債券償付的例子。可贖回債券就是一個例子，在此簡短討論。

由定價函數所得的債券價值為108.5392美元（單元格B12），該值與表14-1中列出的價格相符合（到期收益保留小數點後三位，因而存在微小取整差異）。該債券正好付息。換言之，付息日恰好是計息期的開始。因此，沒有必要進行應計利息調整。

為了舉例說明處理利息支付日之間債券價格的計算過程，考慮圖14-1中所示的票面利率為6.25%、2030年5月到期的債券。利用電子數據表中D列的記載條目，發現單元格D12的債券淨價為161.002美元，該值與表中的價格僅有幾美分的差別。

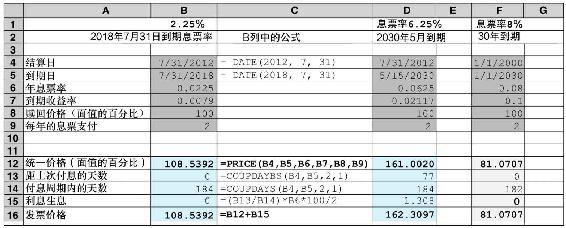
如何計算債券的全價？Excel表中的第13~16行進行了必要的調整。單元格C13中所列出的函數用來計算距上次付息日的天數。該天數的計算是基於債券的結算日、到期日、付息週期（1代表年度，2代表半年），以及計息天數（選擇1代表實際天數）計算得出的。單元格C14中所列函數用於計算每一付息週期中的總天數。因此，第15行中的應計利息條目為半年期利息乘以據上次利息支付的付息週期比例。最後，第16列中的全價為淨價加應計利息。

最後的例子是關於如何獲得例14-2中30年期、票面利率為8%（每半年付息一次）的債券的價格。該例子中給出的市場利率為10%。然而，沒有給出具體的結算日和到期日。此時，仍能利用PRICE函數來對債券定價。簡單的方法是選取任意一個結算日（為方便，選取2000年1月1日），因此設定到期日為30年。電子數據表的F列顯示了合適的結果，結果產生的價格為面值的81.0707%，在F16單元格中。

[1] 以下是一些可能存在歧義的地方。你需要將票面利率與市場利率分清，票面利率決定了將要支付給債券持有者的利息大小，一旦債券發行，它的票面利率就是固定的。而當市場利率增加，投資者不能以較高的貼現率貼現，則這就意味著債券價值及其現值的下跌。

[2] 利率越高，債券價值越低的事實，引起利率增加對價格影響逐漸減少。因此，在初始基數較小的基礎上，利率增加導致價格減少得很小。