e1 Zvi Bodie 投資學 v10
13.5 基於消費的資產定價與股權溢價之謎
在一篇經典的文獻中,梅赫拉和普萊斯考特發現在美國風險資產的超額收益率太高以致其超出了經濟理論和合理的風險厭惡係數所能解釋的範圍。[1]這種現象也被稱為“股權溢價之謎”。關於股權溢價之謎的爭論表明對市場風險溢價的預期要低於其歷史平均水平。歷史收益是否能為未來的收益提供預測的問題非常重要,能為延伸資本市場均衡的討論範圍提供依據。
13.5.1 消費增長和市場收益率
正如第9章所討論的,ICAPM模型衍生於代表性消費者或投資者一生的消費或投資計劃。每個人的計劃是要使其一生的消費最大化,每期的消費或投資取決於其年齡、現有財富、無風險利率以及市場投資組合的風險和風險溢價。
消費模型認為影響投資者決策的不是他們財富本身,而是其一生的消費流。由於一些因素的改變,如無風險利率、市場投資組合風險溢價或大宗消費項目的價格變化,會導致財富和消費之間出現缺口。因此,比財富更好的福利的測度是財富所能提供的消費流。
給定這個框架,基本CAPM的一般化形式就是用證券收益與總消費的協方差來衡量證券風險,而非證券收益與市場收益率(財富的測量)的協方差。因此,我們預期市場指數風險溢價與如下協方差相關:

其中,A是風險厭惡係數的均值;rc是消費-跟蹤證券組合(與總消費增長率的相關性最高)的收益率。(注:該式與傳統CAPM模型中風險溢價的等式E(rM)-rf=ACov(rM,rM)=AVar(rM)類似,然而,在多因素的ICPM模型中,市場不再是均值方差有效的,所以市場指數的風險溢價不再與其方差成比例。APT理論也認為風險溢價與相關因素的協方差呈線性關係,但是因為它忽略了效用假設,並沒對這種關係的斜率進行說明。)
最初的研究試圖直接使用消費數據來估計基於消費的CAPM模型,而非使用追蹤消費的資產組合的收益。大體來說,這些檢驗發現CCAPM對風險溢價的解釋能力並不比傳統的CAPM模型更好。股權溢價之謎的存在說明即使使用合理的A估計,消費增長和市場指數收益的協方差Cov(rM,rC)也會因為太低而不能擬合式(13-10)左邊的市場指數組合超額收益的歷史平均觀測值。(注:傳統CAPM模型沒有類似的問題,在CAPM中,E(rM)-rf=AVar(rM),0.085的風險溢價和0.20的標準差(方差0.04)意味著風險厭惡係數為0.085/0.04=2.125,在合理的範圍內。)因此,風險溢價之謎認為歷史超額收益太高或常用的風險厭惡係數的估計量太低。
近期研究在幾個方面改善了估計方法。首先,使用消費-跟蹤證券組合而非消費增長本身。總消費數據(低頻)僅被用來構建消費-跟蹤證券組合,這些組合的高頻和精確的收益數據被用於資產定價模型的估計(此外,構建追蹤消費的資產組合的任何錯誤都有可能擾亂資產收益和消費風險的關係)。例如,傑加納森和王[2]用每年第四季度的消費構造了消費-跟蹤證券組合。表13-5摘自他們的研究,該表描述了法瑪-弗倫奇因素以及消費貝塔和超額收益率的相關關係。表中上半部分的結果非常熟悉:觀察每一行數據,我們發現賬面-市值比越高的公司其平均收益率越高。相似地,觀察每一列數據,我們發現規模越大的公司其平均收益率越低。表中下半部分的結果卻比較新奇:賬面-市值比較高的公司其消費貝塔越高,規模較高的公司其消費貝塔越低。這意味著法瑪-弗倫奇因素對平均收益的解釋能力事實上能反映資產組合的消費風險。圖13-7顯示了25個法瑪-弗倫奇組合的平均收益與其消費貝塔高度相關。傑加納森和王報告的其他檢驗顯示,法瑪-弗倫奇三因素模型對收益的解釋能力好於單因素CAPM模型但差於CCAPM模型。
表13-5 年超額收益與消費貝塔
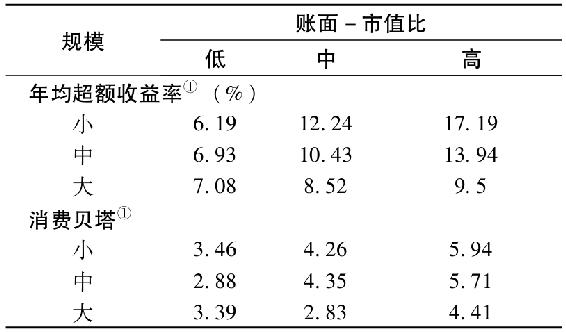
①25個法瑪-弗倫奇資產組合在1954~2003年的平均年超額收益。
消費貝塔由下列時間序列迴歸估計:Ri,t=αi+βi,cgct+εi,t。其中,Ri,t是相對無風險利率的超額收益;gct是用第四季度消費數據計算的年消費增長率。
資料來源:Ravi Jagannathan and Yong Wang,“Lazy Investors,Discretionary Consumption,and the Cross-Section of Stock Returns,”Journal of Finance 62(August 2006),pp.1623-61.
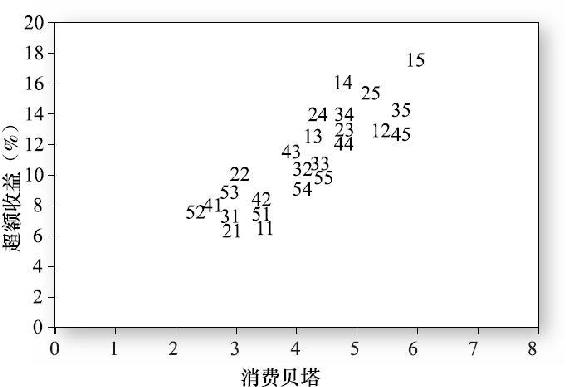
圖13-7 股票收益率的橫截面:25個法瑪-弗倫奇資產組合(1954~2003年)
注:年超額收益和消費貝塔。該圖描出了25個法瑪-弗倫奇資產組合和消費貝塔對應的點。每兩個數結合就代表一種資產組合,第一個數表示規模大小(1——最小,5——最大),第二個數表示賬面-市值比大小(1——最低,5——最高)。
此外,標準的CCAPM模型考察的是代表性消費者或投資者,忽略了投資者擁有不同財富和消費習慣的異質信息。為了提高模型的解釋能力,較新的研究考察了幾類擁有不同財富和消費行為的投資者。例如,對持有金融證券的家庭來說,市場收益與消費將會有更大的協方差。[3]這一發現就部分揭開了股權溢價之謎。
13.5.2 期望收益率與已實現收益率
法瑪和弗倫奇[4]對股權溢價之謎提出了另一解釋。他們使用1872~1999年的股票指數收益率,報告了無風險利率均值、股市收益率均值(標準普爾500指數)以及整體區間和子區間的綜合風險溢價:

由上表,1949年後股權溢價均值顯著增加,說明股權溢價之謎是一個現代的產物。
法瑪和弗倫奇認為用已實現收益率的均值估計風險溢價存在著一些問題。他們採用增長率不變的股利貼現模型(詳見第18章或有關財務方面的入門教材)來估計期望收益率,並發現在1872~1949年,股利貼現模型(DDM)估計的預期風險溢價與已實現超額收益非常相似。但在1950~1999年,DDM估計的預期風險溢價偏小,說明在該區間內,已實現的超額收益均值超過了投資者的預期。
在增長率不變的DDM模型中,股票的預期資本利得率等於股利增長率。因此,股票的預期總收益為股票利率與預期股利增長率g之和:

其中,D1是年末股利;P0是股票的現行價格。法瑪和弗倫奇將標準普爾500指數作為公司的代表,並用式(13-11)估計E(r)。
在每個樣本期間,t=1,…,T,法瑪和弗倫奇計算股票利率(Dt/Pt-1)和股利增長率(Dt/Dt-1-1)之和,從而估計出期望收益率。相比而言,已實現收益率為股票利率與資本利得率(Pt/Pt-1-1)之和。兩個計算式中,股票利率是相同的,期望收益率和已實現收益率的差別就等於股利增長率和資本利得率之差。雖然,股利增長率和資本利得率在早期比較相似,但在現代,資本利得率要比股利增長率大得多。因此,法瑪和弗倫奇推斷,股權溢價之謎至少有一部分是由於現代未預期資本利得率所導致的。
法瑪和弗倫奇認為,股利增長率會比平均已實現資本利得率對投資者的預期資本利得率提供更可靠的估計,他們指出了三點理由:
(1)1950~1999年,平均已實現收益率超過了公司投資的內部收益率,如果這些平均收益率代表了收益的期望值,那麼我們會推斷出公司願意進行淨現值為負的投資。
(2)用DDM估計的收益,其統計精確性要遠高於使用平均歷史收益得出的估計。由已實現收益率計算的風險溢價的標準誤差要遠大於DDM模型得出的估計(詳見下表)。
(3)由DDM模型中導出的報酬-波動性比率(夏普比率)要比從已實現收益率中得出的平穩得多。如果風險厭惡在一定區間內保持不變,我們就有理由預期夏普比率保持平穩狀態。
第2點和第3點理由的證據在下表列示,股利模型(DDM)得出的估計和已實現收益率得出的估計分別列出。

法瑪和弗倫奇的研究為股權溢價之謎提供了很好的解釋,即近半個世紀觀察到的收益率比預期的要高。這也意味著對未來超額收益率的預期會低於歷史平均水平(碰巧的是,他們的文章在1999年出版,隨後出現的低平均收益率表明了該項研究的預見性)。
高特茲曼和伊博森[5]也支持法瑪和弗倫奇的觀點,他們將股票收益率和長期公司債券利率的數據延伸到1792年。這些變量在1792~1925年的描述性統計如下。

這些統計量描述的風險溢價要低於1926~2009年(特別是1950~1999年)這一產生股權溢價之謎的期間的歷史平均水平。[6]因此,法瑪和弗倫奇認為未預期到的已實現收益率在歷史上出現的時間範圍實際上相對較短。
13.5.3 生存偏差
股權溢價之謎源於美國股票的平均長期收益。當美國成為世界上最成功的資本市場時(幾十年前人們還未曾預見到),有很多原因揭示,對風險溢價的估計會受到生存偏差的影響。朱里昂和高特茲曼[7]收集了1921~1996年39個國家的股票市場的資本增長指數,圖13-8顯示美國股市的已實現收益率最高,每年高達4.3%,而其他國家收益率的中位數僅0.8%。此外,與美國不同,許多其他國家的資本市場實際上要麼是永久關閉的,要麼就是長時間關閉的。[8]
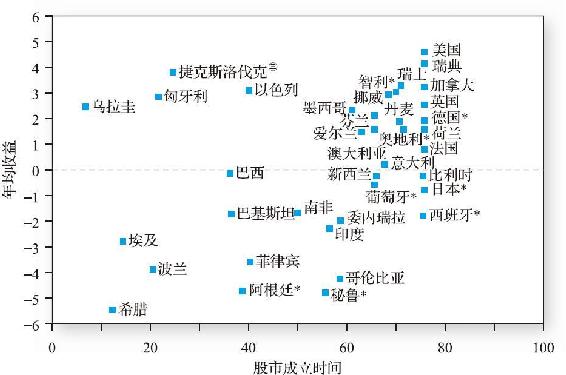
圖13-8 全球39個股票市場1921~1996年的實際收益
注:市場依成立時長分類,圖形顯示成立時間越久的市場,期望收益率越高。*代表該市場曾經歷長期的下跌。
這些結果意味著使用美國股市的平均數據來估計期望收益率受生存偏差的制約,因為與許多其他國家不同,美國股市從未遭過關閉這種嚴重的問題。用最成功的資本市場的經驗估計風險溢價,而忽視資本市場可能在樣本期間關閉的事實,無疑會導致估計的期望收益率偏高。從美國股市中獲得的偏高的已實現股權溢價或許無法表現出必要收益率。
與此類似,在共同基金行業中也存著生存偏差。一些公司會週期性地關閉那些表現最糟糕的共同基金,如果對業績的研究僅考察在全部樣本期間內都存在的基金,那麼估計出的平均收益率也只能反映長期存活下來的基金的業績表現。若將失敗的基金排除在樣本之外,共同基金經理的平均業績表現無疑會比那些考慮所有基金的經理的表現更好。回顧第11章華爾街實戰11-2,如果一個人得到很多關於未來一段時期的股評,並繼續追蹤那些被證實了的股評,由於上述生存偏差的影響,其會發現股評平均來說有一定的預測能力。
13.5.4 CAPM模型的擴展也許能解開股權溢價之謎
康斯坦丁尼德斯[9]認為可以通過放鬆一些假設來擴展標準的CAPM模型,並將觀察到的超額收益考慮進去,特別是當消費者面臨不能確保的特質收入衝擊時,如失業。這種事情在經濟低迷時出現的概率較大,我們需要花很長一段時間去研究資產的收益和方差以及它們隨商業週期的變動。
此外,對生命週期的考察也很重要,這同時也是經常被忽視的一點。生命週期模型中借貸限制的考慮很重要。持有所有股票和債券市場財富的代表性消費者不會面臨借貸限制的問題,但實際上,年輕的消費者的確面臨著這樣的情況。康斯坦丁尼德斯考察了借貸限制對股權溢價、債券的需求以及消費者對資本市場的有限參與的影響。最後,他還將消費者的習慣信息加入到傳統的效用函數,並發現這樣能解釋的風險溢價比通過股票收益和總消費增長的協方差估計的風險溢價更高。他認為將習慣信息、不完全市場、生命週期、借貸限制和其他限制參與股票市場的因素綜合考慮的話,對理性資產定價模型關於資產價格和資產收益的理論和實證研究都非常有益。
13.5.5 流動性和股權溢價之謎
我們已經瞭解到流動性風險對解釋股票的橫截面收益非常重要,非流動性溢價與市場風險溢價可能屬於同一數量級。因此,將市場指數的平均超額收益作為風險溢價自身的估計未免太過簡單。平均超額收益中有一部分是對流動性風險的補償而不僅僅是對收益率波動性的補償。如果認識到這點的話,股權溢價之謎也不會像最初那麼難解了。
13.5.6 股權溢價之謎的行為解釋
巴博里斯和黃[10]認為股權溢價之謎是由非理性的投資者行為導致的。他們考慮的關鍵要素是窄框架和損失厭惡,這也是實驗環境中風險決策問題的兩個著名特徵。窄框架是指投資者將他們面臨的風險孤立地分析,因此,投資者忽視了股票組合風險和其他財富風險的弱相關性,從而要求的風險溢價也會比理性模型預期的要高。再加之對損失厭惡的考慮,儘管傳統理論認為損失厭惡程度較低,但投資者的行為偏差的確會導致較高的風險溢價(詳見第12章關於行為偏差的討論)。
即使當消費增長率平滑移動,並與股票市場弱相關時,將這些因素綜合考慮也能產生一個較大的均衡的股權風險溢價和一個低且平穩的無風險利率。此外,這樣做的話也能得到與獨立貨幣政策態度的可行預測相關的參數。對股權溢價之謎的這些分析還能揭示與之緊密相關的資產組合之謎和股票市場的參與之謎。它們還對未來的研究指明瞭一些可行的方向。
當考慮偏好的異質性時,巴博里斯和黃的方法能解釋為什麼有一部分人希望參與股市卻還避免參與。窄框架還解釋了消費增長和市場收益率之間的分離,單獨分析股票市場的收益率會忽視平滑化和其他對衝策略對消費的有限影響,且損失厭惡會加大相對於基準點的損失帶來的效用減少,進而擴大這種效應。關於這些理論的實證研究的發展能決定股權溢價之謎的有效性和含義。
[1] Jarnish Mehra and Edward Prescott,“The Equity Premium:A Puzzle,”Journal of Monetary Economics,March 1985.
[2] Ravi Jagannathan and Yong Wang,“Lazy Investors,Discretionary Consumption,and the Cross-Section of Stock Returns,”Journal of Finance 62(August 2006),pp.1623-61.
[3] C.J.Malloy,T.Moskowitz,and A.Vissing-Jorgensen,“Long-Run Stockholder Consumption Risk and Asset Returns,”Journal of Finance 64(December 2009),pp.2427-80.
[4] Eugene Fama and Kenneth French,“The Equity Premium,”Journal of Finance 57,no.2(2002).
[5] William N.Goetzmann and Roger G.Ibbotson,“History and the Equity Risk Premium,”working paper,Yale University,October 18,2005.
[6] 短期無風險利率很難評估,因為在這段期間內,短期債券有較大風險且其平均收益率超過了長期公司債券的收益率。
[7] Philippe Jurion and William N.Goetzmann,“Global Stock Markets in the Twentieth Century,”Journal of Finance 54,no.3(June 1999).
[8] 捷克斯洛伐克於1993年分裂為兩個國家。
[9] George M.Constantinides,“Understanding the Equity Risk Premium Puzzle,”in Handbooks in Finance:Handbook of the Equity Risk Premium,ed.Rajnish Mehra(Amsterdam:Elsevier,2008),pp.331-59.
[10] Nicholas Barberis and Ming Huang,“The Loss Aversion/Narrow Framing Approach to the Equity Premium Puzzle,”in Handbooks in Finance:Handbook of the Equity Risk Premium ed.Rajnish Mehra(Amsterdam:Elsevier,2008),pp.199-229.