e1 Zvi Bodie 投資學 v10
13.3 法瑪-弗倫奇式多因素模型
如今佔主流地位的多因素模型是法瑪和弗倫奇[1]提出的三因素模型。法瑪-弗倫奇模型中的系統風險因素有公司規模、賬面-市值比(B/M)以及市場指數。這些額外因素的加入是基於經驗觀察的(見第11章),小公司股票和具有較高股權賬面-市值比(B/M)的股票的歷史平均收益率一般要高於CAPM模型證券市場線的預測值。
然而,法瑪和弗倫奇不僅僅證明了規模和賬面-市值比在解釋收益率中的作用,他們也介紹了一種更普遍的方法生成因素組合,並將這種方法運用到公司特徵研究中。探索這一創新是瞭解多因素資產定價模型實證經驗模塊的有效方法。
假設就像法瑪和弗倫奇,你發現股票市場市值規模(或市值大小)可能在CAPM方程中預測α。一般來看,市值越小,股票α越大。這一發現使得規模因子成為背離CAPM的異象。
但是如果你相信規模將會隨著未來投資機會變動。那麼,單因素CAPM和α一樣將是額外市場多因素CAPM風險的衡量。舉個例子:如果投資者期待市場衰退,他們會調整組合最小化損失敞口。假設小股票一般來說在下降市場中表現更差,蕭條情況下β較大。那麼投資者將會規避這類股票轉而投資較不敏感的大公司股票,這將解釋為什麼小公司風險溢價超過同期市場收益的β。規模大小帶來的α效果或許可以替代ICAPM對未來投資機會衰退更加敏感資產的風險溢價效用。
法瑪和弗倫奇的創新是量化了規模風險溢價。公司規模分佈對稱:少數的大公司和眾多小公司。因為紐約證券交易所是大公司股票交易所,法瑪和弗倫奇首先確定紐約證券交易所中規模位於中位數的股票。使用中位數區分所有交易的美國股票(紐約證券交易所、美國證券交易所和納斯達克)是大還是小的判斷指標,並從大市值中創建組合,從小市值股票中創建另一個組合。最後,每個組合都進行價值加權和分散化。
在APT中,法瑪和弗倫奇通過買小公司、賣大公司構建淨頭寸為0的規模因素組合。這個組合的收益叫作SMB(小公司減大公司),是小公司股票收益與大公司股票收益的差值。如果用價格衡量,那麼這個組合將會擁有風險溢價。因為SMB實際上被充分分散(近似4000只股票)。SMB和規模在兩因素APT模型中被列入市場指數組合,作為市場因素之外的風險因子。在兩因素SML中,風險溢價應該由兩因素組合的風險加載決定,這是可驗證的命題。
法瑪和弗倫奇使用這個方法來構造規模和賬面市值比(B/M)因素。為尋找這兩個市場因素之外的其他風險因子,他們將股票按照規模和賬面市值比進行兩次劃分,並將美國投資者賬戶內股票按照賬面市值比分為三組:下層30%(低)、中間40%(中等)和上層30%(高)[2]。現在基於規模和賬面市值兩因素並考慮較差組合形成六個組合:小市值/低比值、小市值/中等比值、小市值/高比值、大市值/低比值、大市值/中等比值、大市值/高比值。每個組合均價值加權。大市值和小市值組合收益為:
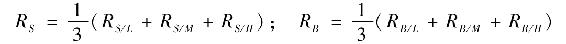
類似地,高比值和低比值(價值股和成長股[3])組合收益為:
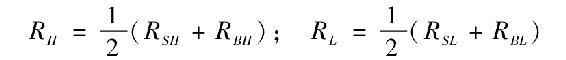
零頭寸因素組合SMB(小市值減大市值,買入小市值賣出大市值)、HML(高比值減去低比值,即買入高比值賣出低比值)由以下組合構建出:
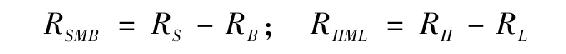
我們衡量個人股票因素敏感度通過估計股票超額收益與市場指數超額收益以及RSMB和RHML的一階迴歸因素β進行。這些因素β可以用於預測整體風險溢價。因此,法瑪弗倫奇三因素資產定價模型是[4]:
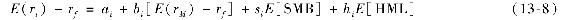
其中,係數bi、si和hi分別是三個因素的股票貝塔,也被稱為因子載荷。根據套利定價模型,如果這些因素是相關的,那麼這些因子載荷導致的風險溢價能夠完全解釋超額收益率。換言之,如果這些因素能完全解釋資產超額收益率,那麼方程中截距項將為0。
戈亞爾[5]對資產定價檢驗進行研究。他將式(13-8)應用到25個由市值和比值劃分的美國股票組合中。圖13-1顯示了每個組合在1946~2010年在法瑪—弗倫奇三因素模型和CAPM(a圖)下實際平均回報率。模擬測試顯示,法瑪—弗倫奇三因素模型比CAPM效果改進很多。
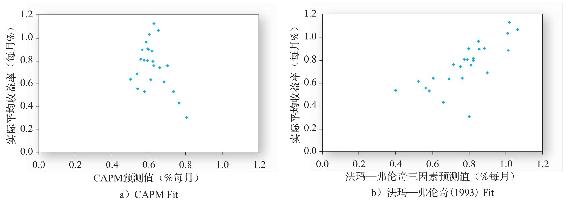
圖13-1 利用CAPM與法瑪-弗倫奇三因素預測值對比結果
資料來源:Amit Goyal,“Empirical Cross Sectional Asset Pricing:A Survey,”Financial Markets and Portfolio Management 26(2012),pp.3-38.
注意在圖13-1a中,預測收益對於所有組合幾乎一樣。這確實是用市值和比值分類組合進行測試的弱點,但是劃分標準不包括β。結果顯示,所有組合β均接近1。加入對β的劃分變成5×5,組合數量從25變為125。雖然這很難處理,但是前沿的計量經濟學和計算方法將會支持這種類型的檢驗研究。
13.3.1 市場規模和賬面市值比作為風險因子
列維和瓦薩羅[6]發現不同風格的組合(HML和SMB)的收益率看似能預測GDP的增長,因此也可能涵蓋了一些商業週期風險。圖13-2中每個條柱都是HML或SMB組合在GDP增長率較高的年份和GDP增長率較低的年份收益率之差的平均值。正值意味著組合在宏觀經濟形勢好的年份表現更好。佔絕大部分的正值也意味著HML和SMB組合的收益與宏觀經濟的未來走勢正相關,從而可作為商業週期風險的代理變量。因此,規模和價值溢價中至少有部分可以反映成是對更高風險敞口的合理補償。
佩特科瓦和張[7]嘗試著將價值型組合(高B/M)的平均收益補償與風險溢價聯繫起來,並使用條件CAPM模型進行檢驗。在傳統的CAPM模型中,我們將市場風險溢價和公司的貝塔視為給定的參數。相比而言,正如我們在前面章節提到的,條件CAPM模型允許這些變量隨時間變化,或隨同一因素變化。如果市場風險溢價高時,股票的貝塔值也高,那麼這種正向聯繫會導致股票風險溢價中的“協同效應”,這是股票貝塔和市場風險溢價共同作用的結果。
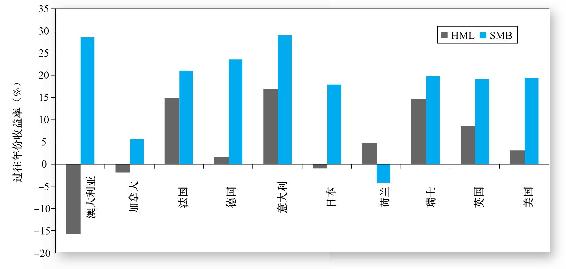
圖13-2 因素資產組合在GDP增長高於平均年份和GDP增長低於平均年份之前的收益率之差
注:在未來有更高GDP增長的年份,SMB和HML組合的收益率一般都更高。
資料來源:J.Liew and M.Vassalou,“Can Book-to-Market,Size and Momentum Be Risk Factors That Predict Economic Growth?”Journal of Financial Economics 57(2000),pp.221-45.©2000 with permission from Elsevier Science.
那麼是什麼導致貝塔和市場風險溢價之間的聯繫呢?張[8]關注不可撤回的投資,發現價值型公司(具有高賬面-市值比)平均會有更多的有形資產。這些不可撤銷的投資會使得這些公司在經濟形勢低迷時面臨更大的風險,因為在嚴重的經濟衰退時,已存在的這些資產會有較大的產能過剩(相比而言,增長型公司能通過將投資計劃延後以更好地面對經濟衰退)。高賬面-市值比的公司在經濟衰退時面臨的更高的風險敞口會導致其在衰退市場中有著較高的貝塔。此外,有證據表明,在跌市中投資者會因經濟壓力更高並變得更加不安,此時市場風險溢價會更高。這兩方面結合起來可能導致了高B/M公司的貝塔和市場風險溢價的正向聯繫。
為了量化這些概念,佩特科瓦和張將貝塔和市場風險溢價都設置為一組“狀態變量”,即能反映經濟狀態的變量:
DIV——市場股利收益率;
DEFLT——公司債的違約利差(Baa~Aaa級利率);
TERM——期限結構利差(10年~1年期國庫券利率);
TB——1個月國庫券利率。
在進行一階迴歸時,將這些狀態變量替代貝塔,具體形式如下:
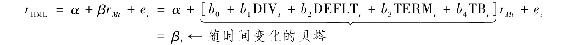
首先通過b4估計出參數b0,再將這些參數和每期四個狀態變量的值擬合出貝塔值,從而估計出每期的貝塔值。
類似地,能用相同的狀態變量估計出隨時間變化的市場風險溢價:
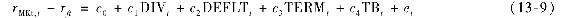
我們能使用迴歸參數和每期的狀態變量值估計出每期的市場風險溢價,迴歸的擬合值就是市場風險溢價的估計值。
最後,佩特科瓦和張檢驗了貝塔和市場風險溢價的關係,他們用溢價的大小來定義經濟狀態,經濟頂峰時期被定義為具有最低1/10的風險溢價的時期,經濟低谷時期是具有最高1/10的風險溢價的時期。結果如圖13-3所示,支持了反週期貝塔的概念:HML組合的貝塔在經濟形勢好時為負,意味著價值型股票(高賬面-市值比)的貝塔要小於增長型股票(低賬面-市值比)的貝塔,當在經濟衰退時會出現相反的情況。雖然HML的貝塔和市場風險溢價的協方差本身還不足以解釋價值型組合的平均收益溢價,但至少有一部分風險溢價是理性的。
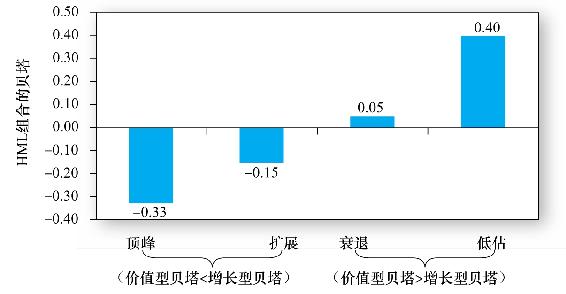
圖13-3 不同經濟狀態下HML組合貝塔
注:當市場風險溢價越高時,HML組合的貝塔也越高。
資料來源:Ralitsa Petkova and Lu Zhang,“Is Value Riskier than Growth?”Journal of Financial Economics 78(2005),pp.187-202.©2005 with permission from Elsevier.
13.3.2 基於行為的解釋
在爭論的另一方,學者認為價值型溢價說明了市場的非理性。爭論的本質在於分析員傾向於將近期表現延伸到未來,從而誇大了具有較好近期表現的公司的價值。當市場意識到這個錯誤時,這些公司股票的價格就會出現下跌。因此,平均來說,“魅力股”,即近期表現良好、價格高且賬面-市值比低的股票的表現一般差於“價值股”,因為對賬面-市值比低的公司來說,高價格意味著投資者的過度樂觀。
圖13-4摘自陳、卡西斯基和蘭考尼肖科[9],其描述了投資者的過度反應。根據公司在過去5年的收入增長率將其從低到高排序並分成10組。在第5年年末,每一組賬面-市值比能夠很好地追蹤股票近期表現(虛線)。期末B/M隨著過去5年增長率的增加而平穩下降,意味著歷史表現被外推並反映在價格中。較高的歷史增長率會導致更高的價格和較低的賬面-市值比。
但是對於5年期初的B/M(實線),其與歷史增長率沒有關係或有正向相關,意味著現今的市值與接下來的增長不相關或反向相關。換言之,具有較低賬面-市值比的公司(魅力股)的收入增長不會比其他公司的更快,也意味著市場忽略了歷史增長不能被外推到未來的證據。賬面-市值比更好地反映歷史增長而非未來增長,從而導致了外推的錯誤。
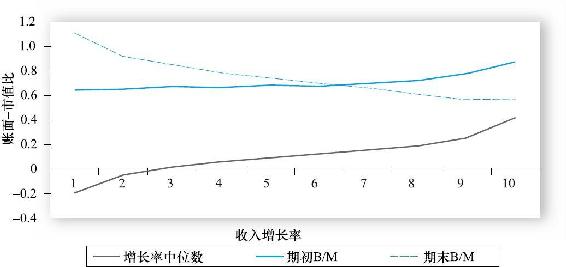
圖13-4 賬面-市值比反映了歷史增長而非未來增長預期
注:5年末的B/M會隨著歷史收入增長率的增加而減少,但會隨著未來收入增長率的增加而出現輕微增加。
資料來源:L.K.C.Chan,J.Karceski,and J.Lakonishok,“The Level and Persistence of Growth Rates,”Journal of Finance 58(April 2003),pp.643-84.Used with permission of John Wiley and Sons,via Copyright Clearance Center.
拉波塔、蘭考尼肖科、施萊佛和維什尼[10]考察了實際盈餘對外公佈時的股價表現,為證明外推的錯誤提供了更多的證據。他們將股票分成價值型和增長型,考察了在分類日後4年的盈餘宣佈後的股價表現。圖13-5表明在盈餘宣佈後,增長型股票的表現要差於價值型股票。從而推斷出,在實際盈餘對外公佈時,已經被歸為增長型的股票的市場表現相對失望一些。
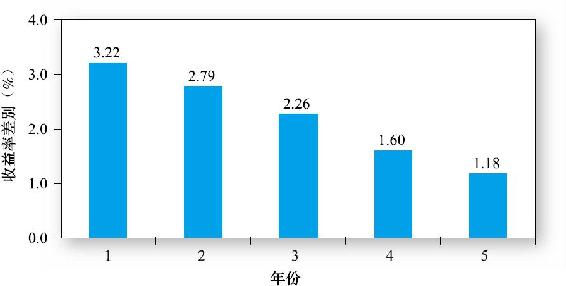
圖13-5 1971~1992年盈餘公佈時,價值股和績優股的表現差別
注:公佈效應每4年在股票被劃分為價值股或績優股之後測量一次。
資料來源:R.La Porta,J.Lakonishok,A.Shleifer,and R.W.Vishny,“Good News for Value Stocks,”Journal of Finance 51(1997),pp.859-874.Used with permission of John Wiley and Sons,via Copyright Clearance Center.
13.3.3 第四個因素:動量
自從法瑪-弗倫奇三因素模型提出後,第四個因素也被加入模型中控制股票的收益行為,即動量因素。如第11章所介紹的,Jegadeesh和Lehmann發現股票較好或較壞的表現會持續幾個月,類似於動量的特性。[11]卡哈特將這種動量效應加入到三因素模型中,並以該模型來評估共同基金的業績。因子以同樣的方法構造,顯示為WML(贏家減去輸家)。這個版本的因子基於過去1~12個月收益選取贏家/輸家。[12]他發現事實上許多共同基金的α值都可以通過因子載荷和對市場動量的敏感性來解釋。原始的法瑪-弗倫奇三因素模型增加一個動量因素就是常用的四因素模型,該模型常被用來評估股票組合的異常表現。
當然,這個額外的因素也帶來了更多的難題。用原始的法瑪-弗倫奇因素來反映風險來源已經有些許挑戰,動量因素使得風險—收益關係的描述更加困難。
[1] Eugene F.Fama and Kenneth R.French,“Common Risk Factors in the Returns on Stocks and Bonds,”Journal of Financial Economics 33(1993),pp.3-56.
[2] 對於這三個賬面市值比組,法瑪和弗倫奇實驗過最優轉折點,但是這種方法很快會帶來數據挖掘問題。
[3] 高賬面市值比股票被稱為價值股,因為它們的市值大都來自已經存在的資產本身。低賬面市值比股票稱為成長股,因為它們的價值大都來自未來預期的增長。當交易資產時需要假設公司高增長來調整價格。與此同時,當公司陷入困境時市價降低賬面市值比增加。因此那些所謂的價值股很可能是陷入困境的公司,從而這類公司可以部分解釋賬面市值因子溢價。
[4] 我們從市場組合收益中扣除無風險利率,而並不從SMB和HML因子收益中扣除,原因在於SMB和HML是淨頭寸為零組合,因子收益已經存在溢價。從無風險投資轉向這類組合投資並不存在機會成本。
[5] Amit Goyal,“Empirical Cross Sectional Asset Pricing:A Survey,”Financial Markets and Portfolio Management 26(2012),pp.3-38.
[6] J.Liew and M.Vassalou,“Can Book-to-Market,Size and Momentum Be Risk Factors That Predict Economic Growth?”Journal of Financial Economics 57(2000),pp.221-45.
[7] Ralitsa Petkova and Lu Zhang,“Is Value Riskier than Growth?”Journal of Financial Economics 78(2005),pp.187-202.
[8] Lu Zhang,“The Value Premium,”Journal of Finance 60(2005),pp.67-103.
[9] L.K.C.Chan,J.Karceski,and J.Lakonishok,“The Level and Persistence of Growth Rates,”Journal of Finance 58(April 2003),pp.643-84.
[10] R.La Porta,J.Lakonishok,A.Shleifer,and R.W.Vishny,“Good News for Value Stocks,”Journal of Finance 52(1997),pp.859-874.
[11] Narasimhan Jegadeesh and Sheridan Titman,“Returns to Buying Winners and Selling Losers:Implications for Stock Market Efficiency,”Journal of Finance 48(March 1993),pp.65-91.
[12] Mark M.Carhart,“On Persistence in Mutual Fund Performance,”Journal of Finance 52(March 1997),pp.57-82.