e1 Zvi Bodie 投資學 v10
13.2 多因素資本資產定價模型與無套利理論的檢驗
三類因子可能增加多因子SML的市場風險因子:①對衝重要消費集合(房屋或者能源)價格不確定性或一般通貨膨脹的因子;②對衝未來投資機會的因子(利率或者市場風險溢價);③對衝資產從市場指數中被剔除的風險因子(勞動力收入或個人經營)。
正如莫頓ICAPM(第9章)中所講,如果有足夠的需求進行對衝這些額外市場資源風險將會產生風險溢價。我們從第三個資源開始研究,因為個人投資組合中非貿易性資產影響人們對可貿易風險資產需求的結論還有些許疑問。因此,代表這類資產的因素,即與這些資產年收益具有相關性的資產,將會影響風險溢價。
概念檢查13-3
a.根據CAPM模型和表13-1中的數據,1946~1955年法瑪-麥克貝思數據迴歸中γ0、γ1、γ2和γ3的估計值分別為多少?
b.如果法瑪和麥克貝思檢驗發現β2和σ(e)的係數為正,該如何解釋這種現象?
13.2.1 勞動收入
被忽略的資產集的兩個主要因素是勞動力收入和個人經營。首先考慮勞動力收入,邁爾斯[1]認為個體都有勞動力收入稟賦,但是隻能投資證券和指數組合。他的模型創造了介於β衡量的貿易指數組合和β衡量的真正市場組合的投資組合,這個組合中包括總勞動力收入。這個模型的結論是SML曲線比簡單CAPM更平緩。大部分情況下收入和市場指數正相關,和市場指數中證券市場價值相比有著實際價值,從指數中去除將使觀測的SML斜率(衡量指數收益率-β關係)在指數組合收益之下。
(注:Asset betas on the index portfolio are likely positively correlated with their betas on the omitted asset(for example,aggregate labor income).Therefore,the coefficient on asset beta in the SML regression(of returns on index beta)will be downward biased,resulting in a slope smaller than average RM.In Equation 9.13 the observed beta of most assets will be larger than the true beta whenever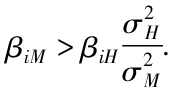 )
)
如果勞動力收入和市場指數並非完全相關,勞動力獲得負收益的可能性將表現為風險沒有全部被指數覆蓋的風險,但是假設投資者可以交易和總資產收益相關的組合,那麼他們對於資產價值波動風險的對衝需求可能會影響證券價格和風險溢價。如果這樣,資產風險(或者一些實證代理變量)就可以加入多因子SML充當額外因子。總勞動力價值為正β的股票將會更多出現在風險因子中。他們將會降低價格,即提供大於CAPM的風險溢價,因此通過增加這個因子,SML也相應變成多維。
傑加納森和王[2]將勞動總收入的變化率作為人力資本變化的代理變量。除了估計資產相對於價值加權股票市場指數的標準貝塔βvw之外,傑加納森和王還估計了資產相對於勞動力收入增長的貝塔βlabor。最後,他們還考察了商業週期對資產貝塔影響的可能性(許多其他的研究也探討過這個問題[3])。這些貝塔也被稱作條件貝塔,因為它們隨著經濟狀態而變化。傑加納森和王將低信用等級公司債和高信用等級公司債的收益率之差作為商業週期的替代變量,並估計了資產相對於商業週期變量的貝塔βprem。估計出每個資產組合的這三個貝塔值之後,傑加納森和王按照式(13-6)進行二階迴歸,模型中包含了公司規模(股權的市場價值ME):
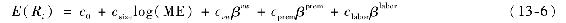
傑加納森和王根據證券的規模和貝塔構造了100個資產組合,並將這些組合作為檢驗樣本。首先根據股票的規模排序並將其分成10個組合,再將每個組合根據貝塔的大小排序並分成10個子組合,這樣就有100個資產組合。表13-2列出了不同二階迴歸的部分結果。表中前兩行是根據法瑪和麥克貝思的CAPM檢驗模型得出的係數和t統計量,顯示的結果是拒絕CAPM模型,因為貝塔的係數值為負,雖然其並不顯著。
接下來的兩行結果說明規模因子的加入並沒有起到任何作用。R2的大幅增加(從1.35%到57%)說明規模能很好地解釋平均收益率的變化而貝塔卻不能。若考慮週期變量和勞動力收入變量而去掉規模變量(表13-2B欄),則模型的解釋力會有所提高(R2為55%),但此時,CAPM模型的期望收益-貝塔關係並沒有得到改善,週期變量和勞動力總收入的係數都顯著。再次加入規模因子(後兩行),我們發現其並不顯著,僅在邊際上提高了模型的解釋能力。
表13-2 評價不同類型資本資產定價模型


注:該表是如下模型的面板迴歸估計(使用了部分或全部解釋變量):
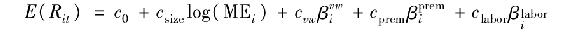
其中,Rit是資產組合i(i=1,2,…,100)在t月(1963.07~1990.12)的收益率;Rvwt是股票價值加權指數的收益率;Rpremt-1是低信用等級和高信用等級公司債的收益率之差;Rlabort是勞動總收入的增長率。βvwi是Rit關於Rvwt最小二乘迴歸的效率係數;其他貝塔也採用相似的方法估計。資產組合規模log(MEi)是組合i中單個資產市場價值對數的加權平均值。迴歸模型用法瑪-麥克貝思方法來估計。“修正的t值”考慮了貝塔估計的樣本誤差。R2為百分數。
儘管結果明顯拒絕了CAPM模型,我們卻能從表13-2中得到兩個重要結論。首先,證券貝塔有條件的一階迴歸估計存在很大缺陷,因為其沒有完全考慮股票收益的週期性,因此不能準確地衡量股票的系統風險。事實上,這對於CAPM模型是好消息,因為我們可用更好的系統風險估計量代替簡單的貝塔值,並將工具變量如規模和經濟週期的解釋能力轉移到指數收益率上。其次,與傑加納森和王的研究相關的是,任何CAPM模型中人力資本都很重要且能更好地解釋證券的系統風險。
13.2.2 非交易性業務
傑加納森和王考慮了勞動力收入,希頓和盧卡斯[4]分析了私營業務的重要性。我們預期私有企業主會減少那些與他們特定企業收入正相關的交易性證券。如果這種效應足夠重要,對交易性證券的總需求將受到這些證券與非公司商業總收入的協方差的影響。那些與非公司業務收入協方差高的證券,其風險溢價也會更高。
與該理論一致,希頓和盧卡斯發現在私營業務上具有更高投資的家庭會減少對股權資產的投資比例。表13-3節選自其迴歸分析,其中整體資產組合中股票的投資比例是被解釋變量。私營業務在總財富中所佔比例(記為“相對業務”)的迴歸係數顯著為負。風險態度(基於自我評估的風險厭惡度)的係數也顯著為負。
表13-3 股票持有比例的影響因素
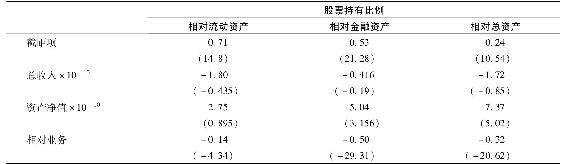
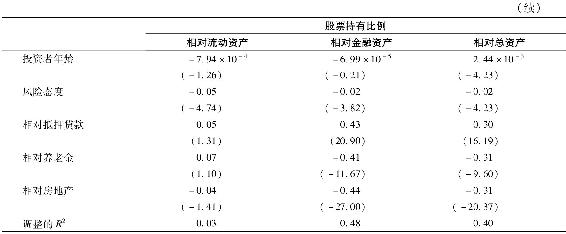
注:標圓括號的數據是t統計量。
資料來源:John Heaton and Debora Lucas,“Portfolio Choice and Asset Prices:The Importance of Entrepreneurial Risk,”Journal of Finance 55,no.3(June 2000),pp.1163-98.Reprinted by permission of the publisher,Blackwell Publishing,Inc.
最後,希頓和盧卡斯還擴展了傑加納森和王的模型,加入了私營業務收入的變化率。他們發現該變量係數顯著且改善了迴歸的解釋能力。此時,市場收益率同樣不能解釋個別證券的收益率,因此CAPM模型的含義仍被拒絕。
13.2.3 多因素資本資產定價模型和無套利理論的早期版本
多因素CAPM模型和APT理論闡述了系統風險敞口如何影響期望收益,但是卻沒有為選擇導致風險溢價的因素提供參考。多因素模型的檢驗包括三個步驟:
(1)風險因素的詳細說明;
(2)辨別規避這些基本風險因素的資產組合;
(3)對解釋能力和套期投資組合風險溢價的檢驗。
宏觀因素模型
陳、羅爾和羅斯[5]提出了一些能代理系統因素的可能變量:
IP——行業生產的增長率;
EI——通貨膨脹的預期變化,由短期國庫券利率的變化測量;
UI——非預期的通貨膨脹,為實際通貨膨脹和預期通貨膨脹之差;
CG——風險溢價的非預期變化,由Baa級公司債和長期政府債券的收益率之差測量;
GB——期限溢價的非預期變化,由長期和短期政府債券的收益率之差測量。
由於辨別了這些潛在的經濟因素,陳、羅爾和羅斯省略了辨別純因子組合(與因素相關性最高的資產組合)的步驟,將因素本身作為替代,此時他們隱含地假設純因子組合能作為因素的替代存在。他們仿照法瑪-麥克貝思方法對這些因素進行檢驗。
這種檢驗方法的一個重要過程就是如何將股票組成資產組合。回顧單因素檢驗,通過構造貝塔值分散化的資產組合來加強檢驗能力。在多因素的框架下,有效組合的標準並沒有那麼明顯。陳、羅爾和羅斯根據規模(流通在外的股票的市場價值,與股票的平均收益率相關)將樣本股組成了20個資產組合。
他們先在一階迴歸中用5年的月數據來估計20個資產組合的因素貝塔值,具體估計是對每個資產組合使用如下的迴歸:
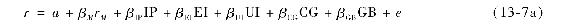
其中,M是指股票市場指數。陳、羅爾和羅斯在此使用了兩個代理變量:價值加權的紐約證券交易所指數(VMNY)和等權重的紐約證券交易所指數(EWNY)。
將20組一階迴歸估計的因素貝塔作為二階迴歸的解釋變量(總共有20個觀測樣本,對應每個資產組合):
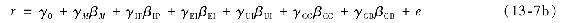
式中,γ是對因素風險溢價的估計。
陳、羅爾和羅斯對樣本期的每月數據進行二階迴歸,且每過12個月就對一階迴歸因素貝塔值重新估計一次。將所有二階迴歸中估計的因素風險溢價(參數γ的值)進行平均。
表13-4列出了一階迴歸的結果,從表中我們可以看出,EWNY和VWNY統計都不顯著(t統計量分別為1.218和-0.633,都小於2),此外,VWNY因素的符號出現錯誤,似乎意味著出現了負的市場風險溢價。行業生產(IP)、公司債券風險溢價(CG)以及未預期到的通貨膨脹(UI)都有著顯著的解釋能力。
表13-4 經濟變量與定價(每月百分比×10)多因素方法

注:VWNY——價值加權的紐約證券交易所指數;EWNY——等值加權的紐約證券交易所指數;IP——行業生產的月增長率;EI——通貨膨脹的預期變化;UI——通貨膨脹的未預期變化;CG——風險溢價的未預期變化(Baa級及以下債券利率減去長期政府債券利率);GB——期限結構的未預期變化(長期政府債券利率減去短期國庫券利率);圓括號標出的是t統計量。
資料來源:Modified from Nai-Fu Chen,Richard Roll,and Stephen Ross,“Economic Forces and the Stock Market,”Journal of Business 59(1986).Reprinted by permission of the publisher,The University of Chicago Press.
[1] David Mayers,“Nonmarketable Assets and Capital Market Equilibrium under Uncertainty,”in Studies in the Theory of Capital Markets,ed.Michael C.Jensen(New York:Praeger,1972),pp.223-48.
[2] Ravi Jagannathan and Zhenyu Wang,“The Conditional CAPM and the Cross-Section of Expected Returns,”Journal of Finance 51(March 1996),pp.3-54.
[3] For example,Campbell Harvey,“Time-Varying Conditional Covariances in Tests of Asset Pricing Models,”Journal of Financial Economics 24(October 1989),pp.289-317;Wayne Ferson and Campbell Harvey,“The Variation of Economic Risk Premiums,”Journal of Political Economy 99(April 1991),pp.385-415;and Wayne Ferson and Robert Korajczyk,“Do Arbitrage Pricing Models Explain the Predictability of Stock Returns?”Journal of Business 68(July 1995),pp.309-49.
[4] John Heaton and Debora Lucas,“Portfolio Choice and Asset Prices:The Importance of Entrepreneurial Risk,”Journal of Finance 55,no.3(June 2000),pp.1163-98.
[5] Nai-Fu Chen,Richard Roll,and Stephen Ross,“Economic Forces and the Stock Market,”Journal of Business 59(1986).