e1 Zvi Bodie 投資學 v10
10.5 法瑪-弗倫奇(FF)三因素模型
現在的主流方法用公司特徵來表示系統性風險相關來源的代表因子,這些特徵在實證層面能作為風險因素的代理變量。也就是說選取作為變量的因素在過去的實證中可以較好地預測平均收益,因此能獲得風險溢價。這種方法最好的例子就是法瑪和弗倫奇的三因素模型[1],它不論在實證研究方面還是業界都受到廣泛關注。
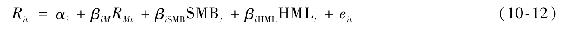
其中,SMB代表小減大,即市值規模小的股票投資組合與市值規模大的股票投資組合的收益差;HML為高減低,即由高賬面-市值比的股票組成的投資組合與低賬面-市值比的股票的投資組合高出的收益差。
注意這一模型中市場指數起著重要作用,它用於測量源於宏觀經濟因素的系統性風險。
選中這兩個公司特徵變量的原因是通過長期的觀察發現,公司市值(公司規模)和賬面-市值比可以用於預測平均股票收益,這與資本資產定價模型的估計相同。法瑪和弗倫奇通過實證方法驗證了這一模型:儘管SMB和HML這兩個變量不是相關風險因素的代理變量,但這些變量可以近似地代替未知的更基本的變量。例如,法瑪和弗倫奇指出,高賬面-市值比的公司更容易陷入財務危機,而小公司對商業條件變化更加敏感。因此,這些變量可以反映宏觀經濟風險因素的敏感度。第13章我們將進一步介紹更多法瑪和弗倫奇模型的實證。
與法瑪-弗倫奇模型相似的實證研究方法,都採用了一些代理變量來描述市場以外的風險來源,這樣導致的一個問題是不能明確指出這些因素對衝的究竟是哪些不確定性。布萊克指出,當研究者為尋找解釋變量而反覆查閱收益的數據庫時(這項活動被稱為數據探測),他們最後可能發現這種“模式”純屬偶然。布萊克[2]發現諸如公司規模這類因素的風險溢價自從首次發現就一直是矛盾的,但法瑪和弗倫奇指出公司規模和賬面-市值比可以預測各時期的世界各地市場的平均收益,因此減輕了數據探測的潛在影響。
法瑪-弗倫奇提出的以公司特徵為基礎的因素提出了這樣一個問題,它們是否反映了一個基於市場外對衝需求的多指數跨期資本資產定價模型,或者反映了一個仍未被解釋的異常情況,其中公司特徵與α值相關。這對解釋該模型來說是需要重點區分的,由於法瑪-弗倫奇模型的有效性可能是由於與合理均衡的背離(由於這裡沒有合理的原因來從這些公司特徵中選擇)產生的,也可能是由於這些公司特徵真的反映了一些與收益相關的風險因素。這一問題需要在第13章中進一步解決。
華爾街實戰10-1 利用套利定價理論確定資本成本
埃爾頓、格魯伯和梅①利用套利定價理論推導出了電力公司的資本成本。他們假定相關風險由一些不可預測的因素構成,例如利率期限結構、利率水平、通貨膨脹率、經濟週期(用GDP衡量)、匯率水平以及他們設計的測量其他宏觀風險因素的指標。
他們的第一步是估計每一風險來源的風險溢價。這一過程通過以下兩步來完成(第13章我們將進一步探討這一方法):
1.估計公司大樣本的“因素負荷”(如β)。計算隨機抽取的100只股票對於系統性風險因素的迴歸收益。他們用時間序列迴歸(如60個月的數據),因此預測了100個迴歸,每隻股票一個。
2.估計每一風險因素的單位回報。將每隻股票每月的收益與5個β進行迴歸分析。各個β係數是隨β值增長而產生的額外平均收益,如以月數據為樣本估計出的該風險因素的風險溢價。這些估計要受到樣本誤差的影響。因此,取每年中12個月估計得到的風險溢價的平均值,這樣可以降低樣本誤差的影響。
下表頂部的中間一欄顯示了風險溢價。
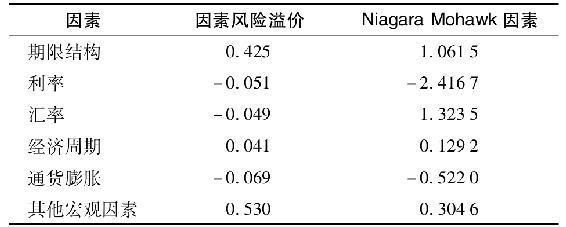
注意一些風險溢價為負值。這一結果的原因在於你不希望受影響的風險因素的風險溢價是正的,而是希望承擔的那些風險因素的風險溢價應該是負的。例如,當通貨膨脹上升時,你希望證券收益上升,並且可以接受那些期望收益較低的證券,此時的風險溢價為負。
因此,任何證券的期望收益與其因素β之間都存在以下關係:
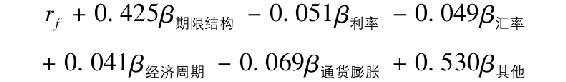
最後,為了獲取某特定公司的資本成本,作者預測每種風險來源的公司β,每一因素β乘以上表中“因素風險的成本”,加總所有的風險來源得到總的風險溢價,並加上無風險利率。
例如,對Niagra Mohawk公司的β估計值位於上表中的最後一欄。因此,它的資本成本等於
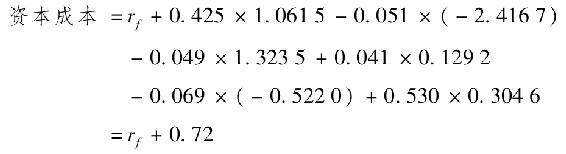
換句話說,Niagra Mohawk公司每月的資本成本比每月無風險利率高0.72%,因此它的年度風險溢價為0.72%×12=8.64%。
①Edwin J.Elton,Martin J.Gruber,and Jiaping Mei,“Cost of Capital Using Arbitrage Pricing Theory:A Case Study of Nine New York Utilities,”Financial Markets,Institutions,and Instruments 3(Auguse 1994),pp.46-68.
[1] Eugene F.Fama and Kenneth R.French,“Multifactor Explanations of Asset Pricing Anomalies,”Journal of Finance 51(1996),pp.55-84.
[2] Fischer Black,“Beta and Return,”Journal of Portfolio Management 20(1993),pp.8-18.