e1 Zvi Bodie 投資學 v10
10.4 多因素套利定價理論
到目前為止我們仍然假設只有一種因素影響股票收益。實際上這條假設過於簡單,因為我們很容易就能想到許多受經濟週期推動可以影響股票收益的因素,如利率波動、通貨膨脹等。可以推測,這些因素會影響股票的風險,從而改變它的期望收益。因此我們可以推導出包含多種風險來源的多因素套利定價理論。
假定我們將式(10-1)中的單因素模型概括為兩因素模型:
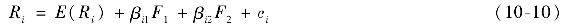
在例10-2中,因素1是GDP實際增長率與期望增長率之差,因素2是未預期利率的變化。每個因素的期望值都為0,因為每個因素都是測度系統變量未預期到的變化而不是變量本身。相似地,公司特有因素引起的非期望收益ei的期望值也為0。構建一個多因素套利定價理論與構建單因素模型相似。
我們可以直接將這樣的兩因素模型發展成多因素模型。但首先我們必須介紹純因子組合(factor portfolio)的概念,即構建一個充分分散的投資組合,其中一個因素的β為1,另一個因素的β為0。我們可以將一個純因子組合看作跟蹤投資組合,即該投資組合的收益跟蹤某些特殊的宏觀經濟風險來源的演變,而與其他的風險來源無關。構建這樣的純因子組合是非常簡單的,因為相對於較少的風險因素而言,我們有大量的證券可供選擇。純因子組合可以作為推導多因素證券市場線的基準投資組合。多因素證券市場線說明對組合產生影響的每個風險因子都對其最後的總風險溢價有其貢獻,貢獻量等於因子β與這一風險來源對因子組合的風險溢價的乘積。我們用一個例子闡述這個事實。
【例10-4】多因素證券市場線
假設有兩個純因子組合1和2,期望收益率分別為E(r1)=10%和E(r2)=12%。進一步假設無風險利率為4%。第一個純因子組合的風險溢價為10%-4%=6%,而第二個純因子組合的風險溢價為12%-4%=8%。
現在考慮一個充分分散的投資組合A,第一個因素的βA1=0.5,第二個因素的βA2=0.75。多因素的套利定價理論表明投資組合的總風險溢價必須等於對每一項系統性風險來源進行補償所要求的風險溢價之和。由於風險因素1要求相應的風險溢價為對投資組合所產生的風險βA1乘以投資組合中第一個因素所產生的風險溢價,因此,投資組合A的風險溢價由因素1產生的風險的補償部分為βA1[E(r1)-rf]=0.5×(10%-4%)=3%,同樣風險因素2的風險溢價為βA2[E(r2)-rf]=0.75×(12%-4%)=6%。投資組合總的風險溢價應該等於3%+6%=9%,投資組合的總收益為4%+9%=13%。
把例10-4中的結論一般化,注意任何投資組合P所面臨的風險因素都由βP1和βP2來表示。可以構建一個與投資組合P相匹配的投資組合Q,該組合由權重為βP1的第一個因素投資組合、權重為βP2的第二個因素投資組合以及貝塔為1-βP1-βP2的國庫券組成。以這種方式構建的投資組合Q與投資組合P具有相同的貝塔,其期望收益為:
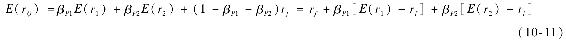
將例10-4中的數據代入,得:
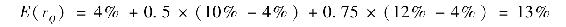
【例10-5】錯誤定價與套利
假設例10-4中投資組合A的期望收益為12%而不是13%,這一收益將會產生套利機會。由純因子組合構建一個與投資組合A具有相同β的投資組合。這要求第一個純因子組合的權重為0.5,第二個純因子組合的權重為0.75,無風險資產的權重為-0.25。這一投資組合與投資組合A具有相同的因素β:第一個因素的β為0.5,因為第一個因素投資組合的權重為0.5;第二個因素的β為0.75(-0.25權重的無風險國庫券不會影響任何一個因素的敏感性)。
現在投資1美元於投資組合Q中,並同時賣出1美元投資組合A。你的淨投資為0,但你的期望收益為正並且等於:
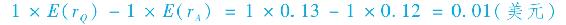
你的淨收益也是無風險的。由於你買進1美元投資組合Q並賣出1美元投資組合A,而且它們都是充分分散的投資組合併有著相同的風險β,風險因素的風險會相互抵消掉。因此,如果投資組合A的期望收益與投資組合Q不同,那麼你可以在淨投資為0的情況下賺得無風險利潤。這就是套利機會。
由於投資組合Q與投資組合A的兩個風險源完全相同,因此它們的期望收益也應該相等。所以投資組合A的收益率也應該為13%。如果不是,將會出現套利機會。[1]
我們可以得出以下結論:如果不存在套利機會,貝塔值為βP1和βP2的充分分散的投資組合一定有式(10-11)給出的期望收益。你可以發現式(10-11)其實是對單因素證券市場線的簡單拓展。
最後,把式(10-11)的多因素證券市場線擴展到單項資產,這一過程與單因素套利定價理論完全相同。除非每一個證券都可以單獨地滿足條件,否則式(10-11)不可能使每一個充分分散的投資組合都滿足條件。因此式(10-11)表示具有多種風險源的多因素證券市場線。
前面已經指出資本資產定價模型的一個應用就是為存在管制的公共事業提供“公平”收益率。多因素套利定價理論也有相同的作用。注意利率與通貨膨脹的風險溢價的經驗估計都為負,與例10-2中所分析的結果相一致。
概念檢查10-3
利用式(10-5)中的因素投資組合,計算β1=0.2、β2=1.4的投資組合的均衡收益率為多少?
[1] 投資組合A的風險溢價為9%(比標準普爾500指數的歷史風險溢價要高),該組合看似是防禦型的,因為其兩個β都小於1。這清楚地說明了多因素與單因素模型之間的一個區別。雖然在單因素市場裡,高於1的β應該屬於進攻型,但這也並非可以預言其在一個多因素的經濟體中屬於防禦型還是進攻型,因為在該經濟體中,風險溢價依賴於所有風險因素的貢獻之和。