e1 Zvi Bodie 投資學 v10: 10.2 套利定價理論

e1 Zvi Bodie 投資學 v10

10.2　套利定價理論

史蒂芬·羅斯^[1]在1976年提出套利定價理論（arbitrage pricing theory，APT）。如同資本資產定價模型，套利定價理論預測了與風險期望收益相關的證券市場線，但其得出證券市場線的方式與之不同。羅斯的套利定價理論基於三個基本假設：①因素模型能描述證券收益；②市場上有足夠的證券來分散風險；③完善的證券市場不允許任何套利機會存在。我們從其模型的簡單形式入手，假定只有一個系統因素影響證券收益。

10.2.1　套利、風險套利與均衡

當投資者不需要進行淨投資就可以賺取無風險利潤時，就存在套利機會。一個典型的例子就是當同一只股票在兩個不同的交易中以不同的價格交易。例如，假設IBM公司股票在紐約證券交易所賣195美元，而在納斯達克僅僅賣193美元。然後你可以在買進納斯達克股票的同時在紐約證券交易所賣出，在不動用任何資本的情況下每隻股票可以賺取2美元的無風險利潤。一價定律（Law of One Price）指出如果兩項資產在所有的經濟性方面均相同，那它們應該具有相同的市場價格。一價定律被套利者所利用：一旦發現違背了這一定律，他們將進行套利活動——在價格低的地方買進資產並同時在價格高的地方售出資產。在這一過程中，他們將促使低價市場價格上揚，而高價市場價格被壓低，直到套利機會消失。

市場價格變動直到套利機會消除，這也許是資本市場理論中最基本的觀點。違背這一原則是市場非理性的明顯表現。

一個無風險套利投資組合最重要的性質是：不管其風險厭惡程度和財富水平如何，投資者都願意持有一個無限的頭寸。由於大量的頭寸使價格上漲或下跌至套利機會完全消除，證券價格將滿足“無套利條件”，也就是停留在一個不存在套利機會的價格水平上。

套利與風險-收益佔優的觀點相比較可以發現，二者在均衡價格的形成上存在著重要區別。風險-收益佔優的觀點認為，當均衡價格關係被打破時，投資者將在一定程度上改變他們的投資組合，這取決於他們的風險厭惡程度。這些有限的投資組合改變的加總將產生大量的買賣行為，從而重建均衡價格。相反，當套利機會存在時，每個投資者都願意儘可能多地持有頭寸，因此不需要很多投資者就會給價格帶來壓力使價格恢復平衡。因此，由無套利論點得出的價格的意義要大於由風險-收益佔優觀點所得到的結論。

資本資產定價模型就是這種佔優觀點的一個典型例子，它意味著所有投資者都持有均值-方差有效投資組合。如果證券沒有被正確定價，那麼投資者在構建投資組合時更傾向於被低估的證券而不是被高估的證券。許多投資者改變自己的投資組合給均衡價格帶來壓力，儘管每個人都是相對較小數量的改變。存在大量均值-方差敏感的投資者對於資本資產模型來說至關重要。相反，無套利條件指的是少量投資者發現投資機會並大量動用自己的資金在短時間內使價格恢復均衡。

從業人員並不像此處的定義一樣對“套利”和“套利者”進行嚴格的區分。“套利者”通常表示在專業領域如併購某目標股票中尋找沒有被正確定價的行為，而不是尋找嚴格意義上（無風險）套利機會的人。這樣的行為通常叫作風險套利（risk arbitrage），與純套利不同。

這裡我們先提及一下，第四部分我們將討論“衍生”證券，例如期貨期權，它們的市場價值完全由其他證券的價值確定。例如，股票看漲期權的價值由股票的價值決定。對於這些證券，嚴格套利是完全可能的，無套利條件將產生精確的定價。而對於股票以及價值不是嚴格地由其他一種或者多種資產所決定的“原始”證券，無套利條件一定要從分散化投資的角度得出。

10.2.2　充分分散的投資組合

下面我們來看在單因素市場中一個股票投資組合的風險。我們首先說明如果一個投資組合是充分分散化的，它的公司特有風險或非因素（系統）風險將可以被分散，只剩下因素（系統）風險。如果我們構建一個n只股票的投資組合，其權重為w_i，∑w_i=1，那麼投資組合的收益率可以表示為：

其中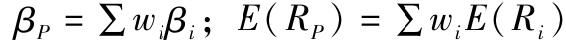，，是n個證券的β_i的加權平均值。該投資組合的非系統部分（與F無關）e_P=∑w_ie_i是n種股票的加權平均值。

我們可以將投資組合的方差分為系統的與非系統的兩個方面：

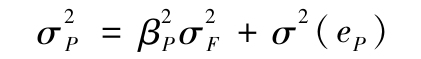
其中σ²_F是因素F的方差，而σ²（e_P）是投資組合的非系統性風險，可以表示為：

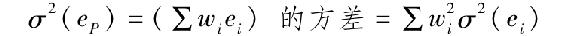
注意到在獲得投資組合的非系統方差時，我們是基於公司特有風險e_i相互獨立的假設，因此投資組合非系統部分e_i的方差是單個非系統方差與投資頭寸的平方的加權之和。

如果投資組合是等權重的，即w_i=1/n，那麼非系統方差應該等於：

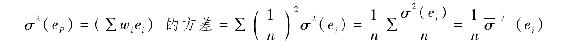
式中最後一項是證券非系統方差的均值。換句話說，投資組合的非系統方差等於非系統方差的平均值除以n。因此，當投資組合變大即n變大時，非系統方差趨近於0。這就是分散化的結果。

對於等權重的投資組合我們得出結論，當n變大時，非系統方差趨近於0。當權重不相等時，這一性質依然成立。任意投資組合都滿足當n變大（準確地說，對於w²_i隨著n的增加趨近於0）時，w_i都逐漸變小，投資組合的非系統性風險趨近於0。實際上，這一性質促使我們來定義充分分散的投資組合（well-diversified portfolio），即按照各自的比例w_i分散投資於數量足夠大的證券，從而降低非系統方差σ²（e_P）從而使之忽略不計。

概念檢查10-2

a.一個投資組合投資於多種股票（n很大）。這些股票殘餘收益的標準差並不比其他的投資組合大。然而，將一半的投資組合投資於股票1，其餘的等量投資於n-1只股票。請問這個投資組合是充分分散的嗎？

b.另一個投資組合投資於同樣的n只股票，n非常大。如果不是等權重的每隻股票佔的投資，而是一半股票佔1.5/n的權重而另一半股票佔0.5/n的權重，那麼這個投資組合是充分分散的嗎？

由於任何充分分散的投資組合的e_P的期望值為0，同時方差也趨近於0，我們可以得出e_P的值實際上也為0的結論。重寫式（10-1），我們得到充分分散的投資組合，在實踐中有：

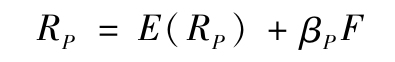
圖10-1a中實線勾畫出在不同的系統性風險下，一個β_A=1的充分分散的投資組合A的收益情況。投資組合A的期望收益為10%，即實線與縱軸相交的點。如果宏觀因素是正的，投資組合的收益將超出期望值；如果是負的，投資組合的收益將低於平均值。因此投資組合的收益率為：

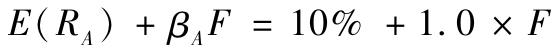
將圖10-1a與圖10-1b相比較，圖10-1b是一隻β_s=1的個股票。它的非系統性風險不能被分散掉，呈現為分別分佈在直線兩側的點。相反，對於充分分散的投資組合，其收益完全由系統因素所決定。

在單因素情況下，充分分化組合的所有配對都是完全相關的：它們的風險完全由相同的系統性因素決定。考慮次等充分分化組合Q，其收益率R_Q=E（R_Q）+β_QF。我們都可以計算出P和Q的標準偏差，以及協方差和相關係數：

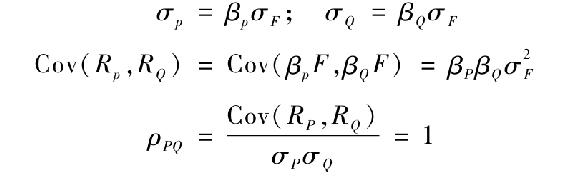
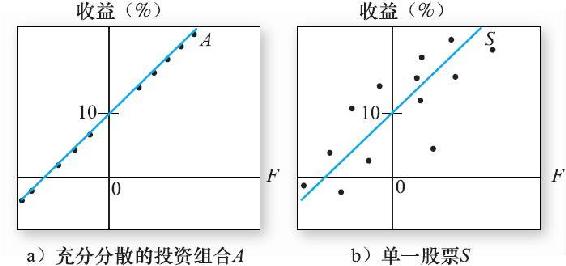
圖10-1　作為系統性風險函數的收益

完全相關是指在一個縱軸是期望收益，橫軸是標準差的描點圖（見圖7-5），任意兩個充分分化的組合構成一條直線。我們之後會看到這條線就是資本市場線。

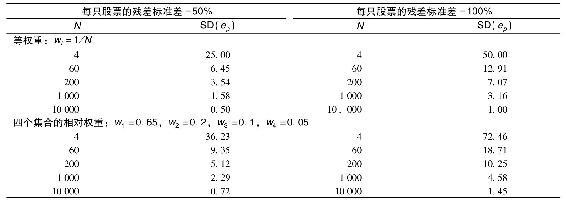
10.2.3　實踐中的分散化和殘差風險

如果實踐中的組合規模是有限的，什麼是組合殘差風險的分散化效果呢？實際上，我們會找到年化的殘差標準差高達50%的大公司股票和甚至高達100%的小公司股票。為了說明分散化的影響，我們考察兩種結構的組合。一種是等權重的，這將使得相同標準差的股票實現最高的分散化效用。作為對比，我們構建一個非等權重的組合。我們選擇4組股票，每組的權重分別為70%、15%、10%和5%。最高的比重是最低的比重的14倍，這將嚴重影響分散化的效用。然而，如果我們用同樣的相對權重加入越來越多的四股組合進行進一步的分散化，我們就可以克服這個問題，這是因為分散化的提高會降低原本最高的組合權重。在一個含有1000只股票的等權重組合中，每隻股票的比重為0.1%；在不等比重的組合中，有1000/4=250個四股組，最高和最低的股票比重分別為70%/250=0.28%和5%/250=0.02%。

什麼是大組合？很多人廣泛地持有交易所交易基金，每個基金都有上百隻股票，有些（像Wilshire 5000）基金有上千只股票。這些組合對於公眾是可以獲得的，因為投資公司的年度支出比例僅為這樣基金訂單提供了10基點的比例。所以1000只股票的組合不是遙不可及的，但是10000只股票的組合的確是很難實現的。

表10-1將組合殘差標準差表達為股票數量的函數。含有1000只股票的等權組合擁有很小但是不可忽略的標準差，當殘差風險為50%時，標準差為1.58%；當殘差風險為100%時，標準差為3.16%，而不平衡的組合的標準差是上述標準差的兩倍。對於10000只股票構成的組合，標準差是可以忽略的。這說明了至少在理論上，如果投資集足夠大的話，即使對於很不平衡的組合，分散化也可以消除風險。

表10-1　等權與非等權組合的殘差方差

10.2.4　實施套利

假設一個單因子市場，充分分散化的組合M代表式（10-1）中的市場因子F。任意證券的超額收益由式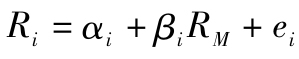決定，則一個充分分散化的組合P（殘差為0）的超額收益滿足：

現在假設證券分析發現組合P有一個正α^[2]。我們同時也可以從宏觀分析中估計得到指數組合M的風險溢價。

由於無論是組合M還是組合P都沒有殘差風險，這兩個組合的唯一風險來源就是系統性的，可以從共同因子的β推導出來（指數的β為1）。所以，你可以消除P的風險：使用P和M構建一個零β組合Z，其中P和M所佔權重分別為w_p和w_M=1-w_p：

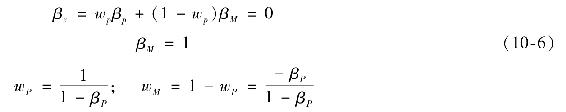
所以組合Z是無風險的，它的α是

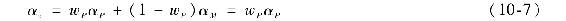
Z的風險溢價一定為0，因為Z的風險為0。如果這個風險溢價不為0，你將可以獲得一個套利利潤。下面說明如何套利。

因為Z的β為0，式（10-5）顯示Z的風險溢價就是α。運用式（10-7）知道α_z為w_Pα_P，所以：

你可以從一個零和投資的套利組合中知道：如果β_P<1且Z的風險溢價是正的（說明Z的收益比無風險利率大），則應借款並投資Z。對於每個借美元投資在Z的人，你將得到一個淨收益（即交付了借款利息之後的收益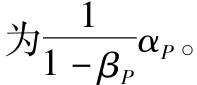）這就是一個造錢機器，所以你會盡力去做（注：在β_P=1處，式（10-8）中的函數變得不穩定。當β_P接近1時，函數值跟α_P同符號接近無窮大。這在經濟直覺上是合理的，因為在這樣的情況下，做多P的頭寸和做空M的頭寸相當，且對於每一美元，你的套利利潤都接近無窮大。）。相似地，如果β_P>1，式（10-8）告訴我們風險溢價是負的，所以，賣空Z並以無風險利率投資。再一次，一個造錢機器被創造出來。然而，沒有一種情況是可持續的。隨著套利者通過大量的交易來追逐這些策略，會推動股價變動直至套利機會消失（即直至組合Z的風險溢價為0）。

10.2.5　套利定價理論的無套利等式

我們已經看到套利活動會很快地將任意零β充分分散組合的風險溢價調至0（注：作為一個聯繫，說明當α_P<0時，你可以顛倒Z中P的頭寸，這樣套利組合仍然可以獲得一個無風險超額收益。）。將式（10-8）調至0會發現任意充分分散化組合的α也必須為0。從式（10-5）可以得知這意味著對任意充分分散化的組合P有：

換種方式說，組合P的風險溢價（期望超額收益）是β和市場指數的風險溢價的乘積。式（10-9）就顯示出了通過套利定價理論的“無套利”要求得到的應用於充分分散組合的資本資產定價模型證券市場線。

APT和CAPM得到相同的SML這一結論在圖像中更為直觀。首先我們解釋為什麼所有具備相同β的充分分散組合必須得到相同的期望收益。圖10-2畫出了兩個組合的收益，A和B的β都是1，但是有不同的期望收益：E（r_A）=10%且E（r_B）=8%。

那麼投資組合A與B能一起在圖中並存嗎？顯然不能：無論系統因素是多少，A的收益高於B，將存在套利機會。

如果以100萬美元賣空B並同時買進100萬美元的A，對於一個淨投資策略，你可以獲取2萬美元的無風險收益，如下：

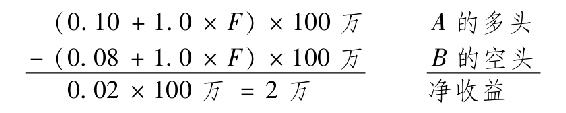
你獲得的是無風險收益，因為因素風險在空頭與多頭頭寸之間被抵消。進一步說，該投資要求零淨投資。你可以用無限大的投資規模直至兩種組合的收益差消失。在市場均衡中，β相等的充分分散的投資組合必須有相同的期望收益，否則存在套利機會。

那麼β值不同的投資組合呢？現在來證明風險溢價必須與β成比例。想知道為什麼，如圖10-3所示。假設無風險利率為4%，C為一個充分分散的投資組合，β等於0.5，期望收益率為6%。投資組合C在無風險資產以及投資組合A線的下方。因此，考慮一個新的投資組合D，一半由投資組合A組成，另一半由無風險資產組成。投資組合D的β=0.5×0+0.5×1.0=0.5，期望收益率=0.5×4+0.5×10=7%。現在投資組合D與投資組合C的β值相同，但有著更高的收益率。從我們前文的分析中可以看出這樣存在套利機會。我們可以得出結論：為了排除套利機會，所有充分分散的投資組合的期望收益必須在圖10-3的無風險資產線上。這條線的方程給出了所有充分分散的投資組合的期望收益。

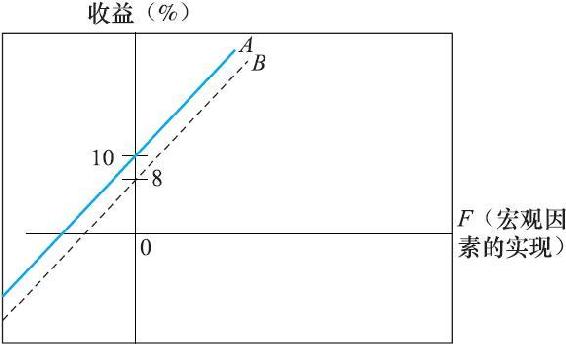
圖10-2　作為系統性風險函數的收益：出現了套利機會

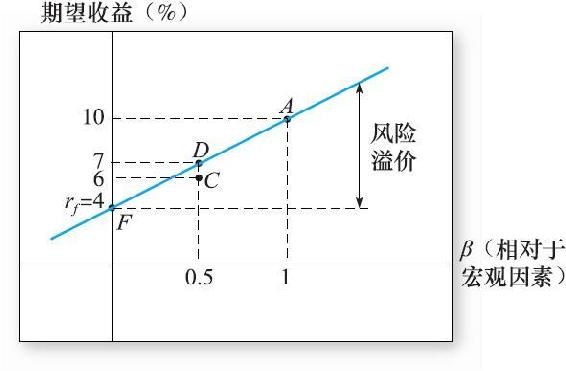
圖10-3　一個套利機會

注意到圖10-3，風險溢價確實與資產β成比例。縱軸表示風險溢價，它由無風險利率與該投資組合期望收益之間的距離來表示。β=0時風險溢價為0，然後隨著β的上升而上升。

[1] Stephen A.Ross，“Return，Risk and Arbitrage，”in I.Friend and J.Bicksler，eds.，Risk and Return in Finance（Cambridge，MA：Ballinger，1976）.

[2] 如果組合α是負的，我們仍然使用下面的策略。我們只需要做空P，就可以獲得和P價值相當的正α，並得到負的β。