e1 Zvi Bodie 投資學 v10
10.1 多因素模型概述
第8章介紹的指數模型提供了一種分解股票風險的方法,即將風險分解為市場或系統性風險和公司特有風險。其中系統性風險主要受宏觀經濟影響,而公司特有風險或特質性風險則可以通過構造投資組合的辦法進行分散。在單指數模型中,市場投資組合收益反映了宏觀因素的重要影響。在第9章中我們介紹了存在這樣的可能性:資產風險溢價可能也與市場外的風險因子,如通脹,或者包含未來投資機會的參數所產生的變化:利率、波動性、市場風險溢價和β。例如,那些收益隨通脹加劇而增加的資產可用於對衝未來通脹率的不確定性,而這種風險溢價會隨投資者對資產需求的增大而降低。
單個證券的風險溢價應該反映它們對額外市場風險因子變化的敏感度,恰如它們相對於市場指數的β決定了它們在基本資本資產定價模型中的風險溢價。當證券可以用於對衝這些因子時,對衝需求就會使SML變為多因子的,其中每個可以對衝的風險來源都會增加一個因子。風險因子不是被這些對衝組合的收益所描述(比如指數組合代表市場因子),就是更直接地被風險因子自身的變化所描述,比如說利率或者通脹的變化。
#證券收益的因素模型
我們首先將考察一個第8章介紹的單因素模型。第8章曾敘述過,資產收益的不確定性有兩個來源:一是公共或宏觀經濟因素,二是公司特有因素。我們用公共因素來度量宏觀經濟中新信息的影響,並定義這些新信息的期望收益為0,因此公共因素的期望收益也應當為0。
如果用F表示公共因素偏離其期望值的離差,βi表示公司i對公共因素的敏感程度,ei為公司特有的擾動項,由因素模型可知,公司i的實際收益應等於它的初始期望收益加上一項反映未預期到的宏觀經濟事件影響的隨機變量(零期望值),再加上另一項反映公司特有事件的隨機變量(零期望值)。
單因素模型(single-factor model)可以用式(10-1)來表示:

其中E(Ri)為股票i的期望收益。注意如果在任何時期宏觀經濟因素都為0(如宏觀經濟沒有很大波動),證券收益等於它先前的期望收益值E(Ri)加上公司特有事件引起的隨機變量。我們進一步假定非系統因素ei均不相關,且與因素F不相關。
【例10-1】因素模型
為了使模型具體化,來分析以下例子。假定宏觀經濟因素F反映所處的經濟週期,這一指標由未預期到的國內生產總值(GDP)變化的百分比來衡量,如果普遍認為今年的GDP將會增長4%,而實際上GDP僅僅增加3%,那麼F值為-1%,代表實際增長與預期增長有-1%的離差。給定股票的β值為1.2,則預期的落空將造成股票收益率比之前預期的收益率低1.2%。這一未預期到的宏觀變化和公司特有的擾動項ei一起決定股票收益對初始期望收益的偏離。
概念檢查10-1
假定在式(10-1)中當前股票的期望收益為10%。許多宏觀經濟信息表明GDP增長為5%而不是4%。你將如何修正該股票的期望收益率?
因素模型將收益分為系統和公司兩個層面是很有說服力的,但將系統性風險限定為由單因素造成的就不那麼有說服力了。實際上在第9章談到將系統性風險作為風險溢價的來源時,我們注意到影響市場收益的系統性或宏觀因素有許多風險來源,如利率或通貨膨脹等的不確定性。市場收益不僅反映了宏觀因素,也能反映公司對這些因素的平均敏感程度。
如果能找到系統性風險的顯示錶達,則有機會發現不同的股票對不同的風險來源敏感性的差異,這使得我們可以對單因素模型進行改進。不難看出包含多個因素的多因素模型(multifactor models)能更好地解釋證券收益。
除用於建立均衡證券定價模型之外,多因素模型還可以應用於風險管理。這一模型創造了一種簡化衡量宏觀經濟風險的方法,並構造投資組合來規避這些風險。
我們從分析兩因素模型開始。假設兩個最重要的宏觀經濟風險——經濟週期的不確定性和利率的波動,我們用未預期到的GDP增長率來描述前者。利率的變化我們用IR來表示。任意股票的收益都受到宏觀風險及其公司自身的風險所影響。因此我們可以用一個兩因素模型來描述某一時間段內股票i的收益率:
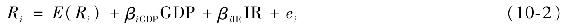
式(10-2)右邊的兩個宏觀經濟因素構成了經濟中的系統因素。正如在單因素模型中,所有的宏觀經濟因素的期望值都為0:這代表這些變量的變化沒有被預期到。式(10-2)中每個因素的係數度量了股票收益對該因素的敏感程度。因此,該係數有時被稱為因素敏感度(factor sensitivity)、因子載荷(factor loading)或因子貝塔(factor beta)。對於大部分公司來說利率上升是壞消息,因此通常利率的β值為負。與前面一樣,ei表示公司特定因素的影響。
為了說明多因素模型的優勢,考慮兩個公司,一個是服務大部分居民區的電力公司,另一個是航空公司。由於居民對電力的需求對經濟週期的敏感程度不高,因此該項對GDP的β值較低,但是電力公司的股票價格可能對利率有著高敏感性。因為電力公司產生的現金流相對穩定,其現值類似於債券,與利率成反方向變化。相反,航空公司股票對經濟活動的敏感程度較高但對利率不是很敏感。因此它對GDP的β值高而對利率的β值低。假設有一天傳出經濟將擴張的消息。預期GDP將會增長,而利率也會上升。那麼這樣的“宏觀消息”是好還是壞?對於電力公司,這是一個壞消息,因為它對利率更敏感。但對航空公司來講,由於對GDP的敏感度更高,這是一個好消息。很明顯,單因素模型或單指數模型不能捕捉這種宏觀經濟不確定性因素變化所反映的差異。
【例10-2】利用多因素模型進行風險評估
假設我們運用式(10-2)的兩因素模型來對東北航空公司進行評估,得到如下結果:
R=0.133+1.2(GDP)-0.3(IR)+e
這告訴我們根據現有的信息,東北航空公司的期望收益率為13.3%,但在當前預期的基礎上GDP每增加一個百分點,東北航空公司股票的收益率平均增加1.2%,而對非預期的利率增加一個百分點,其股票收益下降0.3%。
因素β可以為對衝策略提供一個框架。對於想要規避風險的投資者來說需要構建一個相反的因素來抵消特定風險的影響。通常,遠期合約可以用來對衝這些特定風險因素。我們將在第22章中詳細介紹這方面的內容。
如上所述,多因素模型僅僅是對影響證券收益的因素進行描述。在模型的表達式中並不存在什麼“理論”。很明顯在式(10-2)中存在一個沒有回答的問題是E(r)的來源,換句話說,是什麼決定證券的期望收益率。這裡我們需要一個均衡證券收益的理論模型,所以我們現在轉向套利定價理論來確定等式(10-1)和式(10-2)中的期望收益E(R)。