e1 Zvi Bodie 投資學 v10

9.3　資本資產定價模型和學術領域

假設1（a）（所有資產都是可交易的）讓學者如鯁在喉，因為這將要求有效組合必須包含經濟體中所有風險資產。但在現實中，我們甚至不能觀測到正在交易的所有資產，更不用說那些沒有在交易的。資本資產定價模型的核心，即理論上的市場組合，在現實操作中更是不可能做到的。

因為資本資產定價模型中理論上的市場組合無法觀測，資本資產定價模型的檢驗必須建立在應用於所有可觀測資產的均值-β關係，而這些資產是基於一個可觀測到的，但可能無效的股票指數組合而言的。因而這些檢驗面臨預料之外的障礙。

我們的目標是對證券市場線方程進行檢驗，即E（Ri）=βiRM。在給定時期t對股票超額收益樣本（i=1，…，N）相對於每隻股票β進行迴歸：

資本資產定價模型預測①λ0=0，即樣本中的alpha平均值為0；②λ1=RM，即證券市場線的斜率等於市場指數的風險溢價；③λ2=0，即特異性風險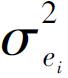無法得到風險溢價。ηi是這個迴歸的零均值殘差。

你可能會問，我們是從哪裡獲得迴歸中的β係數和N只股票的殘差方差的？我們必須從股票收益的時序數據中對每隻股票估計這對參數。這裡的障礙在於：我們估計出來的參數存在很大的偏誤。此外，這些偏誤可能互相相關：首先，每隻股票的β可能和它的殘差方差相關（估計值的偏誤亦然）；其次，迴歸中的殘差項在股票橫截面上可能相關。這些估計偏誤會導致證券市場線的斜率（λ1）偏小，平均α（λ0）偏大。我們甚至不能預測λ2偏誤的方向。

米勒和斯科爾斯[1]的早期論文中已經指出這種偏差的危害性，他們證明了計量問題可能會導致拒絕資本資產定價模型，即使該模型是非常有效的。他們考慮了在模型檢查中可能出現的一系列問題來探究這些問題可能會對結果產生怎樣潛在的影響。為了證明這一點，他們模擬出滿足資本資產定價模型的收益率，並用標準統計方法和這些收益率去“檢驗”模型。儘管這些被模擬的數據滿足資本資產定價模型，但是實證結果拒絕了資本資產定價模型，這一點與用實際數據得出的結論驚人的一致。因此米勒和斯科爾斯證明了計量經濟方法是在現實檢驗中使模型被拒絕的原因。

另一個問題，兩個係數α與β以及殘差都隨著時間的變化而變化。資本資產定價模型中沒有排除這一時間變化的可能性，但是標準迴歸方法卻把它排除在外，因此導致了錯誤地拒絕了模型。現在已經有一些知名的方法來處理時變參數問題。羅伯特·恩格爾因為他在運用計量經濟學的方法處理時變波動性問題取得的突出成就而獲得諾貝爾獎，這些研究已經有一部分運用到金融領域中。[2]此外，貝塔的變化可能不僅僅單純地隨時間變化而隨機變化，它還受整個經濟情況變化的影響。一個“條件”資本資產定價模型允許風險和時間隨一系列“條件變量”的變化而變化。[3]

同樣重要的是，Campell和Vuolteenaho[4]證明了證券的β由兩部分組成：一部分測度了對公司獲利能力變化的敏感度，另一部分測量了市場折現率變化的敏感性。這些改變使結論與以前的大不相同。像本部分簡單介紹的計量經濟方法的改進，可以部分解決簡化資本資產定價模型在實證中出現的問題。

有一部分研究仍未有成果，即尋找組合可以對衝如默頓等式（9-14）中所含特定消費項的價格風險。但是對這個等式基於未來投資機會的實證內容所進行的工作仍然在繼續。

如第5章中提到的那樣，Fama和French提到了規模和賬面市值比具有顯著解釋能力。他們用式（9-14）來解釋和這些性質聯繫在一起的組合作為對衝組合。根據這一思路，其他論文提出了很多其他的超額市場風險因子（在第10章中討論）。但是實際上我們並不知道未來投資機會的哪些不確定性是可以用這些因子對衝的，導致很多學者對實證領域中超額市場對衝組合的識別保持質疑態度。

學術領域達成一致的是單指數資本資產定價模型是過時的。然而，我們仍然不清楚能夠替代這一模型的成功拓展模型是怎樣的。這一部分可以期待在以後的版本中瞭解。

[1] Merton H.Miller and Myron Scholes，“Rates of Return in Relations to Risk：A Re-examination of Some Recent Findings，”in Studies in the Theory of Capital Markets，Michael C.Jensen，ed.（New York：Praeger，1972）.

[2] 恩格爾的論文激發起了ARCH模型的廣泛應用。ARCH代表了異方差自迴歸性，一種表述波動隨時間變化的方法，近來有許多波動性標準用於未來波動的最優估計。

[3] 現在關於條件證券市場均衡模型的文獻有很多。其中大部分來自Ravi Jagannathan and Zhenyu Wang，“The Conditional CAPM and the Cross-Section of Expected Returns，”Journal of Finance 51（March 1996），pp.3-53.

[4] John Campbell and Tuomo Vuolteenaho，“Bad Beta，Good Beta，”American Economic Review 94（December 2004），pp.1249-75.