e1 Zvi Bodie 投資學 v10
9.2 資本資產定價模型的假設和延伸
既然我們已經理解了資本資產定價模型的基本思想，那麼讓我們先討論一下可檢驗的具體含義。一個模型包括①一系列的假設；②運用這些假設對模型進行數學或邏輯上的推導；③一系列的預測。假設所有邏輯和數學推導都是無誤的，我們可以用兩種方法來對模型進行檢驗：規範方法和實證方法。規範方法檢驗模型的假設，而實證方法檢驗模型的預測部分。
如果一個模型的假設是合理的，並且它的推導也是無誤的，那麼模型的預測就一定是正確的。在這種情況下，檢驗模型的假設就等同於模型本身的檢驗。但是就算有的話，也很少有模型能通過規範性檢驗。在很多情況下，像資本資產定價模型，假設都是無效的。我們意識到這些假設確實簡化了現實情況，因此我們都在一定程度上有賴於這些“不正確”的假設。使用這些不現實假設的動機意圖很明確，那就是完全反映真實市場複雜性的模型無解。正如我們注意到的那樣，不光是經濟學需要使用簡化假設，所有科學都面臨同樣的問題。
假設的選取最重要的就是使模型可解，但我們更希望所選取的假設能讓模型更“穩健”。如果一個模型的預測對放鬆某一假設不是高度敏感的話，那麼該模型關於該假設就是穩健的。若僅使用這確保模型穩健性的假設，雖然存在很多缺點，模型的預測的準確性是可以接受的。以上的討論表明模型的檢驗幾乎都是實證性的，即通過檢驗模型實證預測能力來判斷它的有效性。這一規範為所有科學引入統計變量，並要求我們對可接受的顯著性水平和程度設定標準[1]。由於規範性檢驗剔除了非現實的假設，實證檢驗就成了檢驗模型對假設的穩健性程度的一種檢驗。
9.2.1 資本資產定價模型的假設
表9-1列出了資本資產定價模型的一系列假設。至此為止，我們只清晰地提到了這三個假設：
表9-1 資本資產定價模型的相關假設
1.a.投資者都是理性的、執行均值-方差最優化的人。
1.c.投資者使用相同的輸入表，即為同質期望（homogeneous expectations）。
2.a.所有資產都是公開交易的（空頭頭寸是允許的），並且投資者可以使用無風險利率進行借貸。
第一個假設是意義深遠的。其中“可見的”部分是投資者不考慮高階矩（峰度和偏度），而高階矩會增大收益分佈的左尾風險。如第5章中提到，我們可以從對收益分佈正態性統計檢驗來確定這個假設的正確性。
比較難以察覺的是，通過假設投資者只關心財富的均值和方差，假設1（a）排除了資產收益和通脹或者諸如住房和能源等重要消費品的價格之間的關聯。對資產的超額需求可被用於對衝這些“超額市場”的風險，從而增加這些資產的價格，並降低它們基於資本資產定價模型的預測而得的風險溢價。
在一個多期的模型中也會產生相似的超額市場風險，這將要求加上假設1（b），以將投資者決策限制在一個單期的維度。考慮未來利率降低的可能。投資者會因為這將降低他們投資的期望收入而不滿，進而撤資。那些收益與利率負相關的資產（比如長期債券）則因為其可以對衝這一風險而要求更高的價格和更低的風險溢價。由於這樣的對衝需求，任何用以描述未來投資機會的參數關係都將違反資本資產定價模型均值-β等式（並因此與市場組合的有效性之間的關係亦然）。一個單期投資者則消除了這種可能性。
有趣的是，假設1（c）（投資者使用相同的輸入表進行最優化）顯得要求很高，但實際上並沒有那麼大的問題。由於假設2（b）的加入（所有信息都是公開的），投資者決策一般會很一致。此外，使用不同輸入表的投資者的交易行為會相互抵消，從而使價格最終反應一致期望。我們之後會允許部分投資者擁有私人信息，從而根據這些私人信息利用價格偏離的性質。但不論怎樣，在只有公開信息的情況下投資者會假設α值為0這一命題是合理的。
假設2（a），即所有資產都是可交易的，對輸入表這一相同要求是必要的。這將讓我們可以忽略聯邦和州的資產和負債。更重要的是，如人力資本和民營企業這種私人持有但不能交易的資產會導致投資者組合有很大的不同。考慮一個家庭企業的所有者。謹慎心理會導致他們將避免持有和自己的業務高度相關的資產。同理，投資者會避免持有和他們個人收入高度相關的股票。例如，波音的員工應該避免投資航空以及相關行業。這種顧慮所產生的區別化需求將違反均值-β等式，並使指數組合的均值-方差失去有效性。
對貸款的限制（或者對貸款收入很高的利息）違反了假設2（a），並將使資本資產定價模型出現問題。這是因為，貸款人和借款人會得到不同的切線組合，並最終使他們的最優風險組合不同。
稅會導致兩個持有相同股票的投資者最終將實現不同的稅後收益。這樣的扭曲原則上會導致不同的投資者得到不同的稅後最優風險組合。因此需要假設2（c）（不考慮稅）。儘管資本資產定價模型的一種拓展是加入對分紅和資本所得徵收個人所有稅的考慮，沒有決定性的證據表明徵稅對股票收益是一個重要因素。一個可行的解釋是這種負面的發現是由“顧客”和供給效應引起的。如果稅級高的投資者回避那些分紅多的股票，並因而壓低股價，免稅的投資者會視這些股票為一種便宜貨，並抬高對這些股票的需求。此外，如果公司發現分紅多的股票降低了股票價格，它們會將分紅替換為股票回購，促使顧客效應中和徵稅效應。
最後，交易成本會抑制交易和對信息變化的反應，因此需要假設2（b）（不考慮交易成本）。儘管現實中交易成本已經下降，交易成本的分化還是對股票收益有重要影響。
9.2.2 對資本資產定價模型的質疑和拓展
哪些假設是最有問題的呢？基於三個原因，我們從做空比做多難開始：
（1）擁有一項資產空頭頭寸的投資者所揹負的負債可能是無限制的，因為價格可能無止境地上漲。因此一個大的空頭頭寸將要求巨大的抵押，進而這部分抵押將無法被用於投資其他風險資產。
（2）任何提供給做空者的股份供給都是有限的。投資者不能借到股票去做空的情況時有發生。
（3）很多投資公司不被允許做空操作。美國和其他國家甚至使用法規嚴禁做空。
為什麼做空很重要？注意到假設1（a）以“投資者都是理性的……”開始。當投資者對一項資產存在“非理性繁榮”傾向（過度樂觀），則因而價格將上升至高於真實值的地步時，理性投資者就會進行做空，促使股價下跌回歸。然而因為有效的限制，做空無法在股價糾正甚至市場崩潰前抑制價格飆高直到不可持續的水平。這種情況被定義為“泡沫”。
三個不實際的假設2（a）（所有資產可交易）和2（d）（不存在交易費用），結合1（b）（單時期），造成了對模型最大的質疑點。這些質疑促成了一系列的拓展，直至今日，仍然用各種方式“改造中”。由於這個原因，在業界沒有一種拓展形式真正取代了基本資本資產定價模型。這是一個令人印象深刻的現象，儘管模型沒能夠通過一些實證檢驗，資本資產定價模型的邏輯思想在投資領域佔據了核心地位。然而，為了更好地瞭解資本資產定價模型，瞭解模型的拓展形式是有益的。
9.2.3 零β模型
默頓和羅爾[2]分別提出了有效邊界資產組合的一系列有趣特點，其中兩個是：
（1）兩種有效邊界上的投資結合而成的任何資產組合都在其本身的有效邊界上。
（2）有效邊界上的任一資產組合，除去其中的最小方差組合，都在有效邊界下半部分存在一個與其不相關的“伴隨”資產組合。由於這些“伴隨”資產組合不相關，這些伴隨資產組合叫作有效組合的零β投資組合（zero-beta portfolio）。如果我們選擇市場投資組合M和它的零β伴隨資產組合Z，那麼我們可以得到如資本資產定價模型式的公式：
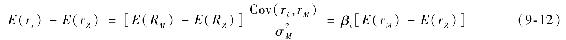
費雪·布萊克[3]用這種性質證明了式（9-12）就是當投資者面臨借入或投資無風險資產限制時資本資產定價模型的形式。在這種情況下，至少某些投資者會選擇有效邊界上風險溢價高的部分。換個方式說，那些想借款並給他們的組合加槓桿的投資者，發現不可行或太昂貴時會傾向於買入高β而避開低β的股票。所以，高β股票的價格會上升，風險溢價下降。證券市場線會比一般資本資產定價模型中更平緩。可以從式（9-12）中看出市場組合的風險溢價更小（因為零β組合的期望收益大於無風險利率），從而承擔β風險的回報變小。
9.2.4 工資收入與非交易性資產
兩項重要的資產是不可交易的：人力資本和私營企業。未來勞動力收入的折現值要遠遠大於整個市場所有可交易資產的總值。私營企業的市場價值也有著同等重要的作用。人力資本和私營企業是兩類不同的資產，同交易證券相比可能有著不同的意義。
私營企業可能是兩類偏離資本資產定價模型的資產中偏離較少的一類。非交易性公司可以被合併或任意出售，或作為流動性資產儲蓄。我們將在第10章中進行討論。私營企業的擁有者也可以以其價值抵押借入資本，從而進一步減少私有公司與公有單位的區別。假設私營企業有著與交易資產相似的風險特徵。在這種情況下，個人可以通過降低他們持有類似證券的資產組合需求來部分抵消其組合多樣化不足的問題。因此，資本資產定價模型的期望收益-貝塔關係不會大幅因私人企業的存在而破壞。
從某種程度上來講，私營企業與交易證券有著不同的風險特徵。一個能對衝特定私營企業風險的可交易資產組合可能出現來自私營企業主的過度需求。這種組合的資產的價格相對於資本資產定價模型而言被抬高，這些證券的期望收益相對於其系統性風險可能較低。相反，與私營企業風險高度相關的證券擁有較高的均衡風險溢價，根據傳統的證券市場線，其α為正值。事實上，Heaton和Lucas[4]已經證明將私營企業主收入引入標準資本資產定價模型能提升它的預測精度。
工資收入的總量以及它的特殊性質對資本資產定價模型的有效性有著重要影響。工資收入對均衡收益的影響可以從它對個人資產組合選擇的重要影響中體現出來。即使個人可以以工資收入作抵押借入資金（房產抵押貸款），以及通過人壽保險來消除未來工資收入的不確定性，人力資本還是很少會被“跨期”交易。運用可交易證券對衝風險要比不可交易的私人企業更困難。這一點可能會給證券價格帶來壓力，並導致與資本資產定價模型的期望收益-貝塔關係相背離。例如，人們為了分散化一定會避免投資於僱主的股票，並且不投資在本行業。因此，人力資本密集型公司的股票需求會減少，這些股票可能要求一個比資本資產定價模型預測的更高的期望收益。
在存在個人不同等級的工資收入（相對於非工資性收入）的情況下，邁耶斯[5]推導出均衡的期望收益-貝塔關係式，其證券市場線方程為：
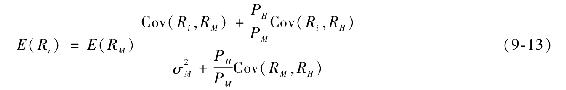
其中，PH為人力資本的價值；PM為交易性資產的市場價值；RH為總人力資本的超額回報率。
資本資產定價模型衡量系統性風險，在擴展模型中用調整後的β值來代替，這個β考慮到了總人力資本的資產組合的協方差。注意到人力資本與所有可交易資產的市值比例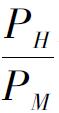
可能大於1，因此證券與工資收入的協方差Cov（Ri，RH）相對於平均值Cov（RM，RH）而言，可能在經濟意義上顯著。如果Cov（Ri，RH）為正值，當資本資產定價模型的β值小於1時，調整後的β值將更大，反之亦然。因為對於一般的證券，我們期望Cov（Ri，RH）為正，小於1時，該模型的風險溢價將比資本資產定價模型預測的大；當證券的β大於1時，該模型的風險溢價將比資本資產定價模型預測的小。因此這個模型給出的證券市場線不如標準的資本資產定價模型陡峭。這也許可以解釋較高β值的證券的α平均為負，較低β值的證券的α平均為正，並導致資本資產定價模型實證上失效。第13章的實證證據將會沿著這條線索給出其他更多的結論。
9.2.5 多期模型與對衝組合
羅伯特·默頓[6]通過使用連續時間模型將資本資產定價模型進行了拓展，給金融經濟學帶來一場革命。雖然他（諾貝爾獎獲得者）對期權定價理論和金融工程（和費雪·布萊克、邁倫·斯科爾斯）的貢獻對投資業有著更大的影響，但他對資產組合理論的貢獻對於我們理解風險-收益關係也同等重要。
在他的基本模型中，默頓提出投資者短視這一假說，他假設所有個體都在優化自己的生命週期消費和投資計劃，並且他們不斷地根據自己的財富水平和退休年齡不斷地調整自己的消費/投資決策。當資產組合收益的不確定性是唯一的風險來源並且投資機會保持不變時，也就是說，市場組合或單個證券的期望收益分佈不變時，默頓所謂的跨期資本資產定價模型（ICAPM）與單期模型預測的期望收益-貝塔關係相同。[7]
但是把額外的風險來源考慮進來時，情形發生了變化。這些額外的風險分為兩大類：一類是關於描述投資機會的參數發生變化，如未來無風險利率、期望收益率或市場投資組合風險。例如，實際利率會隨時間變化而變化。如果實際利率在未來一個時期下降，那麼他的財富水平現在只能支撐一個低的實際消費水平。未來的消費計劃，比如退休支出，可能會陷入窘境。根據一些證券的收益率隨無風險利率變化而變化的程度，投資者將會選擇資產組合來規避風險，從而會抬高這些具有對衝功能的資產價格（並降低收益率）。當其他參數值（本例中的無風險利率）發生不利方向變化時，如果投資者能找到更高收益的資產，他將會犧牲一些自己原計劃的期望收益。
另一類風險的來源是可以用財富購買的消費品價格。來看一下通貨膨脹風險的例子。除了名義財富的期望水平和波動性外，投資者必須關注在生活上的花費——這點錢能買到什麼。因此，通貨膨脹風險是一項市場上重要的風險來源，投資者可能願意犧牲一些期望收益來購買證券，當生活費用增加時，證券的收益率會更高。這樣，可以防止這種通貨膨脹風險的證券需求會影響到資產組合的選擇及其期望收益。我們可以通過此結論進一步得出，對衝需求可能來自消費者支出的子行業，比如投資者可能競相購買能源公司股票價格來規避能源價格的不確定性。這是許多資產規避額外市場風險的特徵。
一般來說，假設定義K為額外市場風險，並找到與K相關的對衝風險資產組合。因此，默頓的跨期資本資產定價模型期望收益-貝塔關係等式將產生多指數形式的證券市場線：
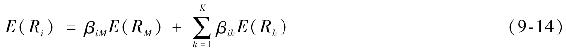
其中，βiM是常用的市場指數資產組合的β，而βik是第k種對衝資產組合的βik。
不受額外市場風險因素影響的其他多因素模型已經導出，並推出跨期資本資產定價模型形式相同的證券市場線。從廣義上來講，這些模型也是資本資產定價模型的擴展形式。我們將在第10章中討論這些模型。
9.2.6 基於消費的資本資產定價模型
資本資產定價模型的原理與上一節提出的對衝需求告訴我們將注意力集中在消費上可能有好處。這樣的模型首先由馬克·羅賓斯坦、羅伯特·盧卡斯和道格拉斯·布里頓提出。[8]
在一個終身消費計劃中，投資者必須權衡各個階段的用於當期消費和用於支撐未來消費的儲蓄和投資。當達到最優時，每增加1美元當前消費所帶來的效用值必須等於該1美元投資帶來未來消費所產生的邊際值。[9]未來財富隨著勞動收入以及投資於該理想資產組合帶來收益的增長而增長。
假設存在風險資產，你希望投資部分儲蓄於風險資產組合來增加期望消費。我們如何來測度這些資產的風險？一般來說，一個單位的收入對投資者的價值在經濟窘迫時（當消費機會匱乏時）要高於經濟富裕時的（當消費機會富裕）。因此一項資產與消費的增長有著正的協方差，那麼從消費的角度來講它的風險就會更大。換句話說，當消費處在很高的水平時，它的回報更大；當消費受抑制時，它的回報越低。因此，與消費的增長有著高協方差的資產擁有更高的均衡風險溢價。根據這一觀點，我們可以將資產的風險溢價寫作“消費風險”的函數：
資產組合C可以被稱為跟蹤消費資產組合（也叫模擬消費資產組合），即與消費增長相關性最高的資產組合；βiC表示資產i的超額收益Ri迴歸於模擬消費資產組合超額收益的迴歸係數；最後，RPC是與消費不確定性相關的風險溢價，它測度的是跟蹤消費資產組合的期望超額回報，即
我們注意到這一結果與普通的資本資產定價模型高度相似。在基於消費的資本資產定價模型中跟蹤消費資產組合起到普通資本資產定價模型中市場投資組合扮演的角色。這是由於該模型更關注消費機會的風險而不是資產組合中單位價值的風險和收益。跟蹤消費資產組合的超額回報同市場投資組合M的超額回報起到同樣的作用，兩種方法都得出線性、單因素模型，差別在於模型中因素的性質不同。
與資本資產定價模型不同，市場投資組合的β在基於消費的資本資產定價模型中時不一定為1。事實證明β大大超過1。這也意味著，在市場指數風險溢價和消費資產組合風險溢價的線性關係中：
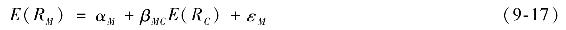
其中αM和εM表示與式（9-15）不符的經驗偏差，βMC不一定等於1。
由於基於消費的資本資產定價模型與資本資產定價模型高度相似，一些人會懷疑它的有用性。確實，正如並非所有資產都具有可交易性導致資本資產定價模型在實證上存在缺陷，基於消費的資本資產定價模型也同樣如此。該模型的吸引力在於它將消費對衝以及可能的投資機會的變換結合起來，即在於單因素框架中的收益分佈參數。當然緊密結合也要付出代價。同金融資產相比，消費增長數據發佈的頻率較低（最多每月一次），並且在測度上存在較大的誤差。儘管如此，最近的研究表明[10]，這一模型相比於資本資產定價模型更能成功地解釋資產的收益，這也是學習投資學的學生需要熟悉這一模型的原因。我們將在第13章中再回過頭來討論基於消費的資本資產定價模型及其經驗證據。
9.2.7 流動性與資本資產定價模型
標準的資產定價模型（如資本資產定價模型）假設市場無摩擦，也就是說證券市場上不存在交易費用。但這些模型都沒有涉及交易活動。例如，在均衡資本資產定價模型中，所有投資者擁有相同的信息和相同的風險資產組合。這一結果的含義是不存在交易動機。如果投資者持有相同的風險資產組合，當新信息出現時，價格會出現相應的變化，但每個投資者依然將繼續持有一組市場投資組合，無須任何資產交易發生。這樣的結果怎樣與日常中的觀測大相徑庭。僅紐約證券交易所每天就會有上億美元的交易發生。一個顯而易見的答案就是異質信念，即沒有整個市場所共享的信念。這些私人信息將會使投資者為獲取更多的利益來根據不同的需求調整自己的資產組合。實際上，交易（和交易費用）對投資者來說非常重要。
資產的流動性（liquidity）是指資產以公平的市場價值賣出的速度及難易程度。流動性的一部分是交易費用問題，特別是指買賣價差。另一部分是價格影響，即當投資者準備進行大額交易時，可能遇到價格反向變動。還有另一個組成部分是及時性——快速售出資產而不用大打折扣的能力。相反，非流動性可以通過一個公平市場的價值折扣部分來衡量，為了使資產儘快出售，人們必須接受這種折價。具有完美流動性的資產在交易時不需要支付這種非流動性折扣。
流動性（或缺乏流動性）一直被看作影響資產價格的一個重要因素。例如，在許多法院的判例中，法院經常對那些不可交易的公司資產大打折扣。可能是由於相對於大宗交易諸如房地產交易的費用來說，證券市場的交易費用微不足道，因此流動性在證券市場上通常不被認為是一個重要因素。Amihud和Mendelson的論文[11]在這一方面有突破性影響。今天，流動性越來越被看作影響價格和期望收益的重要因素。在這裡我們僅僅作一個概要性介紹，第13章中將給出實證證據。
證券交易成本的一個重要組成部分是價差。例如，在電子交易市場，限價指令訂單包括“內部價差”，即在投資者願意賣出的最低價格與投資者願意買入的最高價格之間存在的差距。有效的買賣價差也取決於期望交易的規模。大宗買賣將要求交易者更接近限價指令訂單並接受不太具有吸引力的價格。電子交易市場的內部價差通常會很低，但有效價差可能會非常大。因為絕大多數限價指令只對小額交易起作用。
現在我們越來越強調由於信息不對稱引起的價差部分。信息不對稱是指交易者擁有某一證券價值的私人信息而他的交易對手不知道。為了理解信息不對稱為什麼影響證券市場，我們考慮一下買進一輛舊車所面臨的問題。銷售商比買家瞭解更多的信息，因此買家會自然考慮賣家是不是因為它是“檸檬”而出售這輛車。至少買家會擔心是否支付了過高的價格而將價格調整到他願意為這輛車質量的不確定而支付的價格。在信息不對稱的極端情況下，交易可能完全中止。[12]同理，那些較後提出在限價買賣的交易者會擔心信息更多的交易者對公司真實價值偏離股價時才與他們成交。
總體上來說，投資者交易證券的原因有兩個。一些交易商出於“非信息”動機，例如，出售資產為了一筆大的購置提供資金，或僅僅為了重新調整資產組合。這些交易並不是出於證券價格私人信息而是由於可交易證券的價值驅動的，被稱為噪聲交易。證券交易商在與噪聲交易者的交易中賺取買賣價差從中獲利（他們也可以稱為流動性交易者，因為他們的交易出於流動性的驅動，如現金）。
另一種交易是由買家或賣傢俬人信息驅動的。當交易者相信他們擁有一隻股票被錯誤估價的信息並希望從交易中獲利時，這種交易就會發生。如果信息交易者識別出一次有利的機會，那麼對這個交易的對方來說一定是不利的。如果私人信息顯示一隻股票估價過高，交易者決定要賣掉它，給出買價的交易商或委託限價指令中給出賣價的交易者成為交易中的對手，他們將在事後發現他們買入的股票價格被高估。相反，如果是私人信息導致的買入，證券成交價將在事後發覺低於公平的價格。
信息交易者為證券交易商和下達限價指令的交易者增加了成本。儘管平均來說交易商在與流動性交易者交易時利用買賣價差獲利，但他們在應對信息交易者時遭受損失。相似地，任何交易者的委託限價指令都會由於信息交易者存在而面臨風險。這一結果抬高了委託買價的價格而降低了委託賣價的價格，換句話說，增大了買賣價差。信息交易者影響越大，要求的為彌補潛在損失的價差就越大。到頭來流動性交易者支付了絕大部分信息交易的代價，因為信息不對稱越嚴重，為他們的不知情交易支付的買賣價差越大。
由於非流動性引致的證券價格折扣可能是驚人的，遠遠大於買賣價差。假如某一證券的買賣價差為1%，在將來的3年裡每年被轉手一次，然後被另外一個交易者買入並永久性持有。在最後一次交易中，投資者將支付其公平價格的99.5%或0.995；當股票被賣出時，需要承擔價差一半的費用從而導致價格下跌。第二個買入者知道證券在一年後將以公平價格的0.995賣出，並且不得不承擔另一半的買賣價差，需要支付0.995-0.005/1.05=0.9902（即公平價為0.9902），其中交易費率為5%。最終，當前的買方，當股票以公平價值的0.9902出售時，他就知道明年的損失。他願意為證券支付0.995-0.0098/1.05=0.9857。因此，這種折扣從0.5%摺合到1.43%。換句話說，所有這種遠期的交易費用（價差）將會被折現在當前的價格中。[13]拓展這一邏輯分析，如果證券都是一年交易一次，它當前非流動性交易費用等於當前的費用加上每年0.5%的永續年金，如果年折現率為5%，那麼總共加起來等於0.005+0.005/0.05=0.105或10.5%！顯然，流動性可能有非常大的價值，它在推導均衡資產價格時不容忽視。
交易成本較高，非流動性折價就越高。當然，如果投資者能以較低的價格買入股票，其期望收益率將會更高。因此，我們期望流動性較低的證券將提供較高的平均期望收益。但是非流動性溢價不需要與交易成本成正比。如果一項資產缺乏流動性，那麼交易比較頻繁的交易者應避開該項資產，取而代之的是由很少被高昂交易成本所影響的長期投資者所持有。因此在均衡中，持有期較長的投資者將會更多地持有非流動性證券，而短視的投資者將會偏向於選擇流動性證券。這種“客戶群效應”減輕了非流動性證券的買賣價差影響。最終的結果是流動性風險溢價以遞減的速度隨交易成本（如用買賣價差度量）增加而增加。圖9-4證實了這一預測。
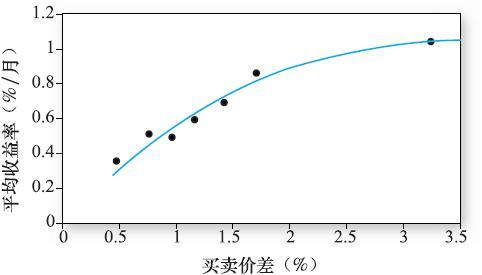
圖9-4 非流動性與平均收益的關係
到目前為止，我們說明了預期流動性水平可以影響價格，進而影響期望收益率。那麼流動性中非預測的變化又會怎樣？在某些情況下，流動性會迅速枯竭。例如，在2008年的金融危機中，由於許多投資者試圖減少槓桿和平倉頭寸，一些資產都很難找到買家。許多抵押證券都停止了交易，流動性突然蒸發了。這也不是從未出現過的現象。從1987年的市場動盪以及1998年長期資本管理公司關閉，也可以看到大範圍的市場流動性降低情況。
事實上，一些文獻利用大的股票樣本研究了多種流動性測度的變化情況，發現當一隻股票的流動性下降時，其他股票的流動性也趨於降低，因此股票流動性呈明顯的相關性。換句話說，流動性的變動是系統性的。毫不奇怪，投資者要求對他們的流動性風險敞口進行補償。這種額外的對承擔流動性風險補償的期望收益改變了期望收益-β的關係。
在上述思路的基礎上，其他作者驗證了流動性變化風險敞口較大的公司是否提供較高的期望收益。[14]例如，Amihud證明了流動性風險較大的公司有較高的平均收益。[15]後來研究關注以“流動性β”來度量的市場流動性風險。與傳統市場β類似，流動性β衡量的是公司收益率對市場流動性變動的敏感程度（傳統β衡量的是收益率的敏感程度）。在市場流動性下降時提高較高收益的公司則能提供對流動性風險的保護，那麼它將被定價較高，因此期望收益率較低。相反，如果流動性與收益率同向變動，那麼流動性風險將會被放大而定價會較低。事實上，正像這些理論所預測的那樣，在第13章中我們將會看到高流動性β的公司將會提供高的平均收益，[16]而且，這些研究表明流動性溢價與市場風險溢價大致具有相同的重要性，這說明流動性應該是證券定價考慮的第一因素。
[1] 為了證明顯著性水平和重要性，我們來看看對一些新藥的功效檢測。檢測藥物可能會出現兩個可能性錯誤。藥物可能是無效的（甚至是有害的），藥檢部門可能認為其是有用的。這個被稱為“第一類錯誤”。這個顯著水平是犯第一類錯誤的可能性。典型辦法就是給定一個顯著性水平，例如5%。在藥物檢驗的例子中，比如第一個檢驗的目標是避免引進無效的或有害的藥物。另一個可能是實際上這個藥物是有效的，但檢驗的結果不是這樣。這一類錯誤叫作“第二類錯誤”，它將會使人們放棄一些有用的藥物。檢驗可以避免犯第二類錯誤的可能。也就是說，如果藥物確實有效時接受藥物的可能性。我們想在一個特定的顯著性水平下測定這種可能性。因此，人們將以高的可能性接受有效的藥物。在特定的社會科學中，有用的檢驗通常有比較低的可能性，在這個檢驗中，他們將會易於接受第二類錯誤，並將會有很高的可能性拒絕一個正確的模型；“這個藥物是有效的”類似於資本資產定價模型的α等於0。當這個檢驗數據拒絕在特定顯著水平下被觀察的α等於0這種假說時，資本資產定價模型將會是無效的。但是，如果檢驗的水平低，當模型是正確的時候我們接受這個模型的可能性將不會很高。
[2] Robert C.Merton，“An Analytic Derivation of the Efficient Portfolio Frontier，”Journal of Financial and Quantitative Analysis，1972.Roll，see footnote 14.
[3] Fischer Black，“Capital Market Equilibrium with Restricted Borrowing，”Journal of Business，July 1972.
[4] John Heaton and Deborah Lucas，“Portfolio Choice and Asset Prices：The Importance of Entrepreneurial Risk，Journal of Finance 55（June 2000）.This paper offers evidence of the effect of entrepreneurial risk on both portfolio choice and the risk-return relationship.
[5] David Mayers，“Nonmarketable Assets and Capital Market Equilibrium under Uncertainty，”in Studies in the Theory of Capital Markets，ed.M.C.Jensen（New York：Praeger，1972）.我們將在後續章節中對此進行詳盡討論。
[6] 默頓的經典的作品收集在Continuous-Time Finance（Oxford，U.K.：Basil Blackwell，1992）.
[7] Eugene F.Fama也在“Multiperiod Consumption-Investment Decisions”上發表了相似的觀點，American Economic Review 60（1970）.
[8] Mark Rubinstein，“The Valuation of Uncertain Income Streams and the Pricing of Options，”Bell Journal of Economics and Management Science 7（1976），pp.407-25；Robert Lucas，“Asset Prices in an Exchange Economy，”Econometrica 46（1978），pp.1429-45；Douglas Breeden，“An Intertemporal Asset Pricing Model with Stochastic Consumption and Investment Opportunities，”Journal of Financial Economics 7（1979），pp.265-96.
[9] 每個時間點的財富等於資產負債表上資產的市場價值加上未來勞動收入。這些消費和投資決策的模型往往能夠使用基於假設投資者表現出持續的相關風險厭惡，或CRRA。CRRA表明在不考慮財富水平的情況下個體投資者最佳風險投資組合中固定比例的財富。你可以回想第6章我們在不考慮財富水平的情況下描述最優投資分配也叫作風險投資組合的最優投資分配。我們採用效用函數的方式來表現出CRRA。
[10] Ravi Jagannathan and Yong Wang，“Lazy Investors，Discretionary Consumption，and the Cross-Section of Stock Returns，”Journal of Finance 62（August 2007），pp.1633-61.
[11] Yakov Amihud and Haim Mendelson，“Asset Pricing and the Bid-Ask Spread，”Journal of Financial Economics 17（1986）.A summary of the ensuing large body of literature on liquidity can be found in Yakov Amihud，Haim Mendelson，and Lasse Heje Pedersen，“Liquidity and Asset Prices，”Foundations and Trends in Finance 1，no.4（2005）.
[12] 2001年的諾貝爾經濟獎得主喬治·阿克爾洛夫（George A.Akerlof）最早研究了市場中的信息不對稱問題，自此之後被稱為“檸檬”問題。對於阿克爾洛夫貢獻的介紹可以在阿克爾洛夫的主頁中找到，An Economic Theorist’s Book of Tales（Cambridge，U.K.：Cambridge University Press，1984）。
[13] 我們將在第13章中看到關於這種交易費用資本化的另一個例子，在此章中對於封閉式基金的大幅折價的一個解釋是每時段成本流的現值很可觀。
[14] 看一個例子，Tarun Chordia，Richard Roll，and Avanidhar Subrahmanyam，“Commonality in Liquidity，”Journal of Financial Economics 56（2000），pp.3-28，or J.Hasbrouck and D.H.Seppi，“Common Factors in Prices，Order Flows and Liquidity，”Journal of Financial Economics 59（2001），pp.383-411.
[15] Yakov Amihud，“Illiquidity and Stock Returns：Cross-Section and Time-Series Effects，”Journal of Financial Markets 9（2002），pp.31-56.
[16] L.Pástor and R.F.Stambaugh，“Liquidity Risk and Expected Stock Returns，”Journal of Political Economy 111（2003），pp.642-685，or V.V.Acharya and L.H.Pedersen，“Asset Pricing with Liquidity Risk，”Journal of Financial Economics 77（2005），pp.375-410.