e1 Zvi Bodie 投資學 v10

9.1　資本資產定價模型概述

資本資產定價模型是基於風險資產期望收益均衡基礎上的預測模型。哈里·馬科維茨於1952年建立了現代投資組合選擇理論。12年後，威廉·夏普[1]、約翰·林特納[2]與簡·莫森[3]將其發展為資本資產定價模型。從馬科維茨的投資組合選擇理論發展到資本資產定價模型經歷了一個較長的過程，這說明資本資產定價模型並不是一朝一夕就可以一蹴而就的。

資本資產定價模型的關鍵是假設所有投資者根據馬科維茨原則最大化組合效用。這就是說，每個投資者都會用一系列的投入組合（期望收益和協方差矩陣）來繪製包含了所有風險資產的有效邊界，從而通過繪出有效邊界的切線CAL（資產配置線）確定一個有效風險組合P，正如圖9-1a所示（與圖7-11相同）。所以，每個投資者在可投資集中持有證券並通過馬科維茨最優化過程來確定持有比例。

資本資產定價模型提出的問題是：如果所有的投資者共享同樣的可投資集並用同樣的投入組合來繪製有效邊界，投資組合選擇將會怎樣？顯然，他們的有效邊界相同。面對同樣的無風險利率，他們會畫出同樣的切線CAL，並自然而然地得到同樣的風險資產組合P。所有投資者因此對每個資產有同樣的持有比例。

資本資產定價模型的一個關鍵觀點是：因為市場組合是所有風險組合的加總，市場組合內的資產比例也是投資者的持有比例。所以，如果所有投資者選擇相同的風險資產組合，這個組合一定是市場組合，即可投資集中所有資產以市值加權平均得到的組合。因而，基於每個投資者最優風險資產組合之上的資產配置線實際上就是圖9-1b所顯示的資本市場線。這個應用讓我們能夠就風險回報權衡做更多的發揮。

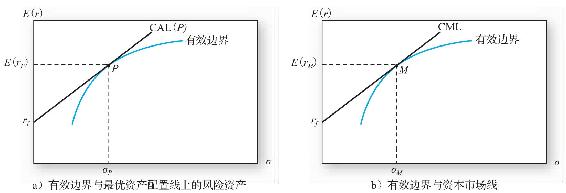
圖9-1　有效邊界和資本市場線

9.1.1　為什麼所有投資者都持有市場組合

什麼是市場投資組合？當我們把單個投資者的資產組合加總起來時，借與貸將會互相抵消（因為每一個借入者都有一個與之相對應的貸出者），其加總起來的風險資產組合的價值等於整個經濟中的全部財富，這就是市場投資組合，用M表示。每隻股票在這個資產組合中所佔的比例等於股票的市值（每股價格乘以公司股票總股數）佔股票總市值的比例。[4]

這意味著，如果通用電氣公司的股票在每一個普通的風險資產組合中所佔的比例為1%，那麼該股票在整個市場投資組合中所佔的比例也是1%。這一結論對每一個投資者的風險資產組合中的任一股票都適用。結果，所有投資者的最優風險資產組合只是圖9-1中市場投資組合的一部分而已。

現在假定投資者的最優資產組合中不包含某些公司的股票，例如不包括德爾塔航空公司的股票，當所有投資者對德爾塔航空公司股票的需求為0時，該股票的價格將會相應下跌。當這一股價變得異乎尋常得低廉時，相比於其他股票，它會變得對投資者有吸引力。最終，德爾塔航空公司的股價會回升到這樣一個水平，使德爾塔航空公司的股票完全可以被接受進入最優的股票資產組合。

這樣的價格調整過程保證所有股票都被納入最優資產組合當中，這說明了所有的資產都必須包括在市場投資組合之中。唯一的區別在於在怎樣的價位上投資者才願意將一隻股票納入其最優資產組合。

9.1.2　消極策略是有效的

在第6章，我們定義資本市場線為資本配置線，它是由貨幣市場賬戶（或短期國債）和市場投資組合構成的，現在你大概可以清楚地看出：為什麼說資本市場線是資本配置線的一個有趣特例。在資本資產定價模型的簡單形式中，市場投資組合M是有效邊界與資本市場線的切點。

在這裡，所有投資者持有的市場投資組合都建立在相同的輸入表之上，因此它們能體現出證券市場中所有的相關信息。這意味著投資者無須進行復雜的證券分析而直接持有市場投資組合及可得到的有效資產組合（當然，如果每個人都採用這樣的資產組合而沒有人進行證券市場分析工作的活，以上情形也就不復存在了，關於這一點，我們將在第11章的市場有效性中再做詳盡的討論）。

因此，投資於市場指數組合這樣一個消極策略是有效的，為此，我們有時把這一結論稱為共同基金原理（mutual fund theorem）。共同基金原理就是曾在第7章討論過的分散化投資的另一種形式。如果所有投資者可以自由地選擇持有與市場組合相同的風險組合，他們不會反對將市場中的股票替換為一個持有市場組合的共同基金所持有的股票。

概念檢查9-1

如果只有少數投資者進行證券分析，而其他人都選擇持有市場投資組合M，那麼證券的資本市場線對於未進行證券分析的投資者而言還仍然是最有效的嗎？為什麼？

在現實中，不同的投資管理者確實創立了很多不同於市場指數的風險資產組合。我們認為這部分是由於在最優資產組合中不同的輸入表造成的。儘管如此，共同基金原理的重要性在於它為投資者提供了一個消極投資的渠道，投資者可以將市場指數看作一個合理的、最有效的資產組合。

華爾街實戰9-1是一個關於指數化爭論的寓言。如果消極策略是有效的，那麼它們傾向於證明交易和研究費用沒有減少收益，也沒有產生不好的結果。

華爾街實戰9-1　貨幣市場基金經理的寓言

幾年前，有個地方叫印地西亞，革命推翻了社會等級制度並引起了私人財產產權體系的重建，原有的政府企業以公司的形式重組，緊接著發行了股票和債券，這些證券通過某一特定中心機構發行，出售給個人、退休基金和其他類似的機構（市場上都流通新印的鈔票）。

許多資產管理者立即開始幫助這些投資者。回想起一位退休老人在革命前的言論（“在印地西亞公司投資”）。他呼籲客戶拿出資金來購買所有新上市的證券。投資者認為這是一個不錯的主意，很快每個人都持有一些印地西亞公司的股票。

不久資本管理者開始感到厭煩，因為他們沒有什麼可做的，很快他們開始習慣於聚集在海濱的賭場裡靠玩輪盤、擲骰子等來消磨時光，並用他們自己的錢賭上一把。

之後，賭場老闆想出一個新主意，他想提供一系列令人印象深刻的房間專門作為基金經理俱樂部。這些會員以不同的公司、工廠、國民生產總值水平、外貿等來打賭，為了使賭博更刺激，賭場的老闆建議他們用客戶的資金作為賭資。

這一建議很快被採納，基金經理饒有興趣地來參加這種遊戲。在每週末，一些基金經理髮現他們為客戶贏了錢，而其他人卻輸了錢，但損失卻遠遠超過了盈利，因為其中一部分花費是賭博的場地費。

不久，一些印地西亞大學的教授指出投資者沒有得到很好的服務，由於基金經理把錢用在俱樂部賭博：“為什麼付錢給別人去賭博，為什麼不自己持有印地西亞公司的份額呢？”

一些投資者認為這一觀點有道理，並且對基金經理提出意見。一些基金經理接受了意見並聲明他們從此將遠離賭場，用客戶的資金按適當的比例投資公司發行的股票和債券。

一開始那些繼續頻繁進出俱樂部的人只是避開轉變為基金管理人，但是隨後，拒絕接受變成了敵對。正如人們所預期的那樣，清教徒式的改革浪潮沒有實現，賭博仍然是合法的。許多管理者繼續把賭場看作自己的聖地，只是他們比以前有了更多的節制，投入小一點的賭注，漸漸地與他們的責任相一致，甚至有些法律俱樂部的成員也發現很難反對賭博，這一活動仍在繼續。

此後，除了賭場業主，每一個人都過得很開心。

資料來源：William F.Sharpe，“The Parable of the Money Managers，”The Financial Analysts’Journal 32（July/August 1976），p.4.Copyright 1976，CFA Institute.Reproduced from The Financial Analysts’Journal with permission from the CFA Institute.All rights reserved.

9.1.3　市場組合的風險溢價

在第6章中，我們討論了個體投資者如何確定投資於風險資產組合的資金金額這一問題。如果所有投資者選擇投資於市場組合M和無風險資產，我們怎樣確定市場投資組合M中的均衡風險溢價？

前面已提出，市場投資組合的均衡風險溢價與投資者群體的平均風險厭惡程度和市場投資組合的風險是成比例的。現在我們可以來解釋這一結論。

概念檢查9-2

從過去80年（見表5-3）標準普爾500指數數據得到如下數據：平均超額收益為7.99%，標準差為23.2%。

a.如果這些平均數近似地反映投資者在這段時間的期望收益率，那麼投資者的平均風險厭惡係數是多少？

b.如果風險厭惡係數的實際值為3.5，那麼符合市場歷史標準差的風險溢價是多少？

假設每位投資者投資於最優資產組合M的資金比例為y，那麼有：

其中，E（rM）-rf=E（RM）是市場組合的風險溢價（期望超額收益）。

在簡化形式的資本資產定價模型的經濟中，無風險投資包括所有投資者之間的借入和貸出，任何借入頭寸必須同時有債權人的貸出頭寸來平衡。這意味著所有投資者之間的淨借入與淨貸出的總和為0，因此，這替代了代表性投資者的風險厭惡係數A，對A而言，風險資產組合的平均比例為100%，或y=1。設y=1，代入式（9-1）整理，我們發現市場投資組合的風險溢價與其方差和平均風險厭惡水平有關。

9.1.4　單個證券的預期收益

資本資產定價模型認為，單個證券的合理風險溢價取決於單個資產對投資者的所有資產組合風險的貢獻程度。資產組合風險對於投資者而言，其重要性在於投資者根據資產組合風險來確定他們要求的風險溢價。

由於所有投資者採用相同的輸入表，這意味著他們的期望收益、方差和協方差都相同。正如第7章提到的那樣，我們可以用邊界的協方差矩陣以及市場組合的權重來計算市場組合的方差。我們在刻畫市場組合中的n只股票基礎上突出GE，從而測算出GE對市場組合風險的貢獻。

如前所述，我們通過將協方差矩陣的所有元素加總來計算資產組合的方差，首先要將行與列的所有資產組合權重相乘。因此，每隻股票對資產組合方差的貢獻率可以表示為股票所在行協方差的總和。這裡每個協方差都要首先乘以每隻股票所在行和列的權重。[5]

所以，通用電氣公司股票對市場組合方差的貢獻為：

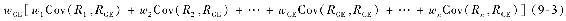
注意到方括號裡的每一項都可以重新表達為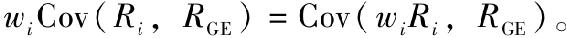此外，由於協方差的可加性，方括號中的項之和為：

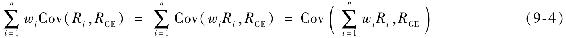
因為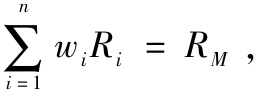所以式（9-4）表明：

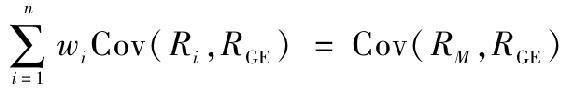
所以，通用公司股票對市場投資組合方差的貢獻程度可以簡單地表示為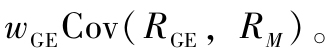

我們對這一結果並不感到驚訝。例如，如果通用公司股票與市場上其他股票的協方差為負，那麼該股票對市場投資組合的貢獻是“負的”：因為通用電氣公司股票的收益率與市場上其他股票收益率的變動方向相反，所以與整個市場投資組合的收益率變動也相反。如果協方差是正的，那麼通用電氣公司股票對市場投資組合風險的貢獻也是正的，其收益率的變動幅度與整個市場投資組合的收益率變動一致。

同時也可以看到，我們持有通用電氣公司股票對整個市場投資組合的風險溢價的貢獻為wGEE（RGE）。

因此，投資通用電氣公司股票的回報-風險比率可以表達為：

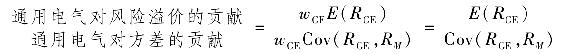
市場投資組合是切線（有效均值-方差）上的資產組合。投資於市場投資組合的回報-風險比率為：

式（9-5）中的比率通常也叫作風險的市場價格（market price of risk），（注：使用這一術語，就會使我們把自己帶入含糊不清的境地，因為投資組合的報酬-波動性比率，有時被稱為風險的市場價格。注意由於合理的計量通用電氣公司風險的方法是用它對市場投資組合的協方差（它對市場投資組合方差的貢獻），所以這個風險是以平方的百分比衡量的。相應地，風險的價格［E（rM）-rf］/σM，被定義為每單位百分比方差平方的期望收益百分比。）因為它測度的是投資者承擔投資風險時所要求的收益。注意有效組合的組成部分，比如通用電氣公司的股票，我們用其對資產組合方差的貢獻程度來測度風險（取決於與市場投資組合的協方差）。相反，對於有效組合本身來說，方差就是最合適的風險測度。

均衡的一個基本原則是所有投資者應該具有相同的回報-風險比率。如果某一投資的回報-風險比率大於其他投資，投資者將會調整他們的資產組合，傾向於賣掉或者選擇不投資於這些股票。這樣的行為會給證券價格帶來壓力直至這一比率相等。因此，我們可以得出通用電氣公司股票的回報-風險比率應該與市場組合的相等：

為了測算通用電氣公司股票的合理風險溢價，我們將式（9-6）稍微變換一下得到：

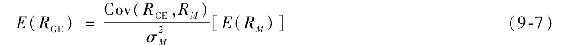
這裡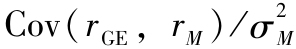這一比率衡量了通用電氣公司股票對市場投資組合方差的貢獻程度，是市場投資組合方差的組成部分。這一比率也叫作貝塔，用β表示。這樣，式（9-7）可以表示為：

這個期望收益-貝塔關係（expected return-beta relationship）就是資本資產定價模型最為普通的一種表達方式。

如果期望收益-貝塔關係對任何單獨資產都成立，那麼它對資產的任意組合都一定成立。假設資產組合P中股票k的權重為wk，k值為1，2，…，n。對每隻股票均引用式（9-8）的資本資產定價模型，並乘以它們各自在資產組合中所佔的權重，每隻股票可以得到以下等式：

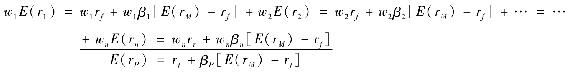
將上式每一行進行加總即得出所有資產組合的資本資產定價模型，因為這裡E（rP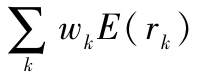）=是資產組合的期望收益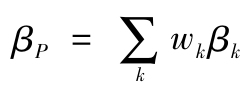，是資產組合的貝塔值。另外，這一結果對市場組合本身也是有效的：

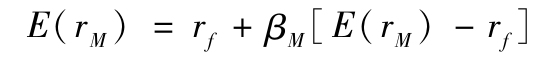
事實上由於βM=1，這確實是一種重複，可以用下式來證明：

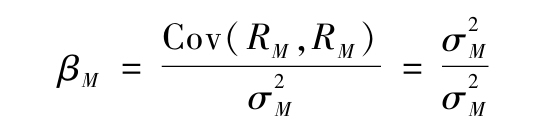
這也證實了所有資產貝塔的加權平均值為1。如果市場貝塔為1，並且市場投資組合是整個經濟中所有資產的組合，那麼所有資產的加權平均貝塔值必定為1。因此如果貝塔大於1，那麼就意味著投資於高貝塔值的股票要承擔高於市場平均波動水平的風險，貝塔值小於1就意味著投資趨於保守。

值得注意的是：我們已經習慣說管理水平較高的企業會取得高的收益水平。我們說這是對的，如果測度公司收益水平高低是基於其廠房和設備等設施所得到的結果。然而資本資產定價模型預測的是公司證券投資的收益。

我們假定每個人都認為某個公司運營良好。相應地，該公司的股票價格將會上升，結果購買該股票股東的投資收益率會隨著股價的不斷上升而無法取得超額收益。換句話說，證券市場價格已經反映了有關公司市場前景的一切公開信息，因此只有公司的風險（正如資本資產定價模型中β值所反映的一樣）會影響到期望收益率。在一個運作良好的市場中，投資者想要獲取高的期望收益率必須要承擔高的風險。

當然，投資者不能直接看出或確定證券的期望收益。然而，他們可以觀察證券價格並通過出價來影響證券價格的變化。相比於某些投資可累計現金流，期望收益率由投資者必須支付的價格來決定。

概念檢查9-3

假定市場投資組合風險溢價的期望值為8%，標準差為22%。假設一個資產組合的25%投資於豐田汽車公司股票，75%投資於福特汽車公司股票，它們各自的β值分別為1.10和1.25，那麼該資產組合的風險溢價為多少？

9.1.5　證券市場線

我們可以把期望收益-貝塔關係視為收益-風險等式。證券的貝塔值之所以是測度證券風險的適當指標，是因為貝塔與證券對最優風險組合風險的貢獻度成正比。

風險厭惡型投資者通過方差來衡量最優風險資產組合的風險。所以我們認為，單項資產的期望收益或風險溢價取決於其對資產組合風險的貢獻程度。股票的貝塔值測度的是它對市場組合方差的貢獻程度。因此，所要求的風險溢價是關於貝塔值的函數。資本資產定價模型論證了這一直覺，並進一步表明證券的風險溢價與貝塔值和市場投資組合的風險溢價成正比，即證券的風險溢價等於β［E（rM）-rf］。

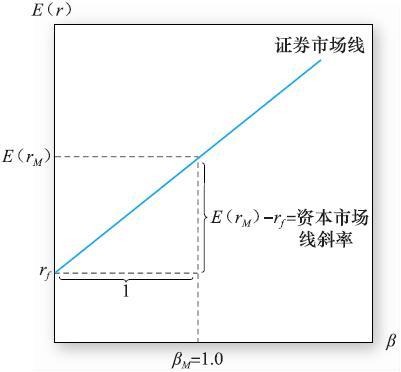
圖9-2　證券市場線

期望收益-貝塔關係就是證券市場線（security market line，SML），如圖9-2所示。因為市場的貝塔值為1，其斜率就是市場投資組合的風險溢價，橫軸為β值，縱軸為期望收益，當橫軸的β=1時，這一點就是市場投資組合的期望收益率。

有必要對證券市場線和資本市場線進行比較。資本市場線描繪了有效資產組合的風險溢價（有效資產組合是指由風險資產和無風險資產構成的資產組合）是資產組合的標準差函數。標準差可以用來衡量有效分散化的資產組合，即投資者總的資產組合的風險。相比較而言，證券市場線刻畫的是單個風險資產的風險溢價，它是該資產風險的一個函數。作為高度分散化資產組合一部分的單項資產的風險測度並不是資產的標準差或方差，而是該資產對資產組合方差的貢獻程度，我們用貝塔值來測度這一貢獻程度。證券市場線對有效資產組合和單項資產均適用。

證券市場線為評估投資業績提供了一個基準。給定一項投資的以β值來測度的風險，證券市場線就能得出投資者為了補償風險所要求的期望收益和貨幣的時間價值。

由於證券市場線是期望收益-貝塔關係的幾何表述，所以“公平定價”資產一定在資本市場線上；也就是說，它們的期望收益與其風險是相匹配的。根據前文所給出的假定，在均衡市場中所有證券都必須在證券市場線上。然而，我們在這裡還想研究資本資產定價模型在貨幣資金管理行業上的應用。假定證券市場線是用來估計風險資產正常期望收益率的基準，證券分析旨在推算證券的實際期望收益率（注意我們現在脫離簡單的資本資產定價模型，來討論某些投資者依據自己的獨特分析運作不同於其他競爭對手的一個“輸入表”）。如果一隻股票被認為是好股票或者被低估的股票，那麼它將提供超過證券市場線給定的正常收益的超額期望收益。被低估的股票期望收益值將會高於證券市場線所給出的正常收益值：在給定貝塔值的情況下，其期望收益高於根據資本資產定價模型所得出的收益值。被高估的股票的期望收益低於證券市場線上所給出的正常收益值。

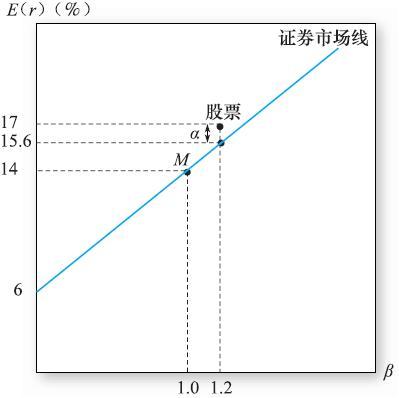
圖9-3　證券市場線和一隻α值為正的股票

股票的實際期望收益與正常期望收益之間的差，我們稱為股票的阿爾法（alpha），記作α。例如，如果市場收益率為14%，股票的貝塔值為1.2，短期國債利率為6%，通過證券市場線計算得出的股票期望收益率為6%+1.2×（14-6）%=15.6%。如果某投資者認為這隻股票的期望收益率為17%，那麼其α值為1.4%（見圖9-3）。

有人認為證券分析（如第五部分所示）是找出α非零的證券。這一分析顯示資產組合管理的起點是一個消極的市場指數資產組合。資產組合管理者將增加α大於零的證券的比例，減小α小於零的證券的比例。我們在第8章中已經給出調整資產組合權重的方法。

資本資產定價模型同樣適用於資本預算決策。一個企業如果打算投資新項目，資本資產定價模型給出了基於貝塔值的必要收益率，這一收益率是投資者可以接受的。管理者可以運用資本資產定價模型得到該項目的內部收益率（IRR）或“必要收益率”。

華爾街實戰9-2描述了資本資產定價模型是怎樣運用在資本預算中的，同時也提出了一些與此結論相違背的異常現象，我們將會在第11~13章進行詳細的討論。

華爾街實戰9-2　來自遙遠的傳說

金融市場風險定價決定了公司的投資方向。但是如果市場是無效的，那將會產生怎樣的結果呢？

投資者很少因為良好的投資直覺而被予以肯定。但是在過去的20年中，越來越多的公司決策時依賴的模型是基於“投資者是理性的”這一前提。如果投資者是非理性的，那麼他們的決策都是錯的嗎？

一個被稱為“資本資產定價”的模型被廣泛應用於現代金融領域。幾乎所有的投資者都希望守住自己的項目，如守住一個商標、一個工廠或一家公司的併購項目，這一切都必須部分地根據資本資產定價模型來判斷自己的決策是否合理。因為該模型為投資者提供了計算必要收益率的方法。如果股東想獲益，任何投資項目的收益率都必須超過其“必要收益率”。

儘管資本資產定價模型較為複雜，但可以簡化為以下五個方面：

（1）投資者可以通過分行業分地區的分散投資方法來規避某些風險，比如工人罷工風險、老闆辭職風險等。

（2）某些風險，例如全球性經濟衰退，是不能通過分散投資的方式來消除的。所以，即使將所有股票納入資產組合籃子，也仍然是有風險的。

（3）相比於投資諸如國債等安全性更高的資產，人們更傾向於投資於風險更高的資產組合。

（4）某項特定投資的收益僅僅取決於其影響市場投資組合風險的程度。

（5）一般來說，可以通過一種簡單的方式來測度其影響市場投資組合風險程度——複製“貝塔”，貝塔表示該項投資的風險與市場投資風險的關係。

正是由於貝塔值使資本資產定價模型變得如此意義重大。儘管投資者面臨著許多風險，進行分散投資的投資者只需要關注那些與市場投資組合有關的風險。貝塔值不僅僅告訴管理者如何測度這些風險，也告訴管理者如何將其直接轉化為必要收益率。如果某項目的未來收益率沒有超過必要收益率，那麼投資者是不值得去投資的。

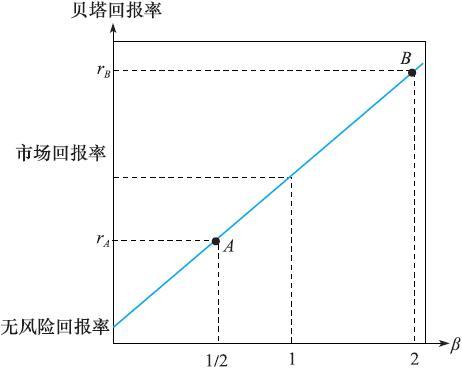
上圖說明了資本資產定價模型是如何工作的。安全性的投資，如國債投資，其貝塔值為0。風險水平較高的投資項目比無風險資產要獲得更高的回報，並且隨貝塔值增加而增加。那些風險與市場風險大致相匹配的投資，其貝塔值為1，根據定義，這些投資應該達到市場收益水平。

因此假設一個公司正在考慮兩個投資項目——A和B。項目A的貝塔值為0.5，即當市場收益上升或下降10%時，其收益也相應地上升或下降5%。因此，它的風險溢價僅為市場收益的一半。項目B的風險溢價是市場風險水平的兩倍，因此通過調整資產組合可以獲得一個更高的收益。

永遠不要故意低估資產

資本資產定價模型仍存在一個小問題：金融學家研究表明貝塔值對於解釋公司股票收益率並不是十分有效。更重要的是，還有更好的指標來解釋這些收益問題。

這一指標就是公司的淨資產（資產負債表上的價值）與市場價值之比。有些研究發現，一般來說，擁有高的淨市率的公司長期收益率較高，即便在調整了風險的貝塔值之後仍然如此。

淨市率效應的發現在金融經濟學家之間引起了廣泛的爭論。所有人都認為有些風險應當獲得更高的風險補償。但是他們在如何測度風險這一問題上產生了嚴重的分歧。一些人認為由於投資者是理性的，淨市率效應必然會引來額外的風險因素。他們因此總結出管理者應該把賬面市場比率考慮進他們要求的必要收益率中。他們還把這一可能出現的必要收益率稱為“期望收益的新估計”，或NEER。

然而，另一些金融學家對此提出了質疑。由於沒有明顯的額外風險與高淨市率相關聯，他們認為投資者會被這一概念誤導。簡而言之，他們低估了高淨市率的股票，這使他們獲得了超額收益。如果這個公司的管理者試圖躍過這些被抬高了的必要收益率，他們就得放棄許多可獲利的資產組合。經濟學家的意見並不一致，那些盡職盡責的管理者會怎樣呢？

來自麻省理工學院商學院的經濟學家傑里米·斯坦給出了一個二者兼顧的答案。①如果投資者是理性的，那麼貝塔值並不是測度風險的唯一方法，所以管理者並不應該採用這種方法。相反，如果管理者是非理性的，貝塔值在許多情況下仍是有效的測度工具。斯坦先生認為如果貝塔測度的是市場基礎風險，這個基礎風險是指它對市場投資組合風險的貢獻，那麼管理者關注它是值得的，即使在某些情況下並未取得理想的結果。

通常，但並非總是如此，斯坦先生的理論中暗含著一個關鍵的區別，即提高公司的長期價值與提高公司股票價格之間的差別。如果投資者是理性的，那麼兩者是一致的：任何提高公司長期價值的決定都會迅速提高股票價值。但是如果投資者正在犯可預見的錯誤，那麼管理者就必須做出決策了。

舉例來說，如果他今天希望提高股價，可能的原因是他希望賣掉股票或者阻止公司被接管的企圖，他通常需要使用期望收益的新估計量，來糾正投資者的錯誤觀點。但是如果他想提高長期價值，他通常會繼續使用貝塔。斯坦先生把這種與NEER不同的方法稱為“市場基礎風險”法，或FAR法。

斯坦先生的結論無疑會惹怒許多公司的老闆，這些老闆經常會怒斥投資者缺乏遠見。他們之所以斥責資本資產定價模型的方法，是因為這一方法假定投資者的判斷無誤，而這個假定前提在決策時起到了關鍵性的作用。但現在如果他們是對的而投資者是錯誤的，則那些有遠見的管理者將是資本資產定價模型最大的追隨者了。

①Jeremy Stein，“Rational Capital Budgeting in an Irrational World，”The Journal of Business，October 1996.

資料來源：“Tales from the FAR Side，”The Economist Group，Inc.November 16，1996，p.8.©The Economist Newspaper Limited，London.

【例9-1】資本資產定價模型的應用

資本資產定價模型的另一個應用是關於效用率的確定。[6]這裡是指在限制投資用途的前提下，確定投資工廠和設備所必要的投資收益。假設股東的初始投資是1億美元，股票的貝塔值為0.6，如果短期國債利率為6%，市場風險溢價為8%，那麼股東投資1億美元所要求的利潤率為6%+0.6×8%=10.8%，或要求的利潤額為1080萬美元。企業應該根據這一利潤水平來確定價格。

概念檢查9-4

XYZ股票的期望收益率為12%，風險β=1，而ABC股票的期望收益率為13%，β=1.5。市場的期望收益率為11%，rf=5%。

a.根據資本資產定價模型，哪隻股票更值得投資？

b.每隻股票的α各是多少？畫出證券市場線並在圖中標出每隻股票風險回報點和α值。

概念檢查9-5

無風險利率為8%，市場投資組合的期望收益率為16%，某項投資項目的貝塔值為1.3。

a.這一項目的必要收益率是多少？

b.如果該項目的期望IRR=19%，是否應該投資該項目？

9.1.6　資本資產定價模型和單指數市場

資本資產定價模型的關鍵應用可以歸納為以下兩點：

（1）市場組合是有效的。

（2）一個風險資產的風險溢價與它的β值成正比。

即使這兩點經常被認為是互補的，但實際上由於它們可以相互轉換，兩者是替代關係（一個成立當且僅當另一個成立）。我們已經解釋過從市場組合有效性到平均β等式這一方向。我們現在用第8章中討論的指數模型市場結構來考察從平均收益-β關係到市場組合有效性這一方向。

從一個單指數市場來推導資本資產定價模型其實更加直觀。相比起以往從假設所有投資者都對相同的投入表應用馬科維茨原則，現在我們假設投資者都面臨這樣一個市場，其中股票超額收益Ri，符合正態分佈，且這個超額收益由單一系統性因素引起。宏觀因子的影響則假設是被一個涉及眾多股票的、按市值加權平均的股票指數組合M來捕捉的。

由式（8-11）可知任意一隻股票的超額收益，所以我們從這個等式出發。

ei是對每個公司特異性的、以0為均值的殘差項，並與股票和市場因素RM無關。殘差代表分散化的、非系統性的，或者特異的風險。一個股票的總風險由系統性影響βiRM的方差和ei的方差衡量。總而言之，風險溢價（平均超額收益）和方差為：

一個用N只股票（用k=1，…，N來排序）對應權重集wi構成的組合Q，其收益一定符合式（9-11），即組合α、β和殘差是其組成證券相應參數的加權平均。

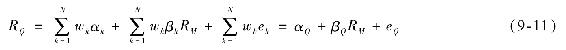
投資者在組建他們的投資組合時有兩方面的考慮：第一，他們會分散非系統性的風險。因為殘差項相互之間是無關的，所以殘差風險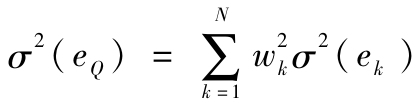會因分散化減小了組合權重比例而更小。第二，Q的風險溢價會因為選擇正α的股票或者做空負α的股票而增加。

基於上述考慮，投資者會毫不猶豫地購買正α的股票，並做空負α的股票。因此，正α股票的價格會增加，而負α股票的價格會降低。這樣的趨勢會持續到所有股票的α值達到0。在這一點上，投資者會滿足於通過完全消除特異性風險來最小化風險，即通過持有儘可能廣泛的市場組合。當所有股票的α都為0時，市場組合是最優風向組合。

[1] William Sharpe，“Capital Asset Prices：A Theory of Market Equilibrium，”Journal of Finance，September 1964.

[2] John Lintner，“The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets，”Review of Economics and Statistics，February 1965.

[3] Jan Mossin，“Equilibrium in a Capital Asset Market，”Econometrica，October 1966.

[4] 正如前面所提到的，為了方便我們使用“股票”作為整個經濟中的代表；市場投資組合恰好包括經濟中的所有資產。

[5] 另一個同樣有效的計算通用電氣公司對市場方差貢獻的方法是求出通用電氣公司所在行與列的元素總和。在本例中，通用電氣公司的貢獻是式（9-3）中的兩倍。我們在書中所提及的方法，以一種便利的方式在證券中分配對投資組合風險的貢獻。每一股貢獻的總量與總的投資組合的方差相等，而這裡所說的另一種方法是把投資組合的方差加倍。這一結果從雙倍計量中得出，因為對每隻股票，把行和列分別相加，將導致矩陣中各元素增加兩倍。

[6] 這一應用越來越少見了，因為許多州放寬了它們對公共事業的管制，很大程度上允許市場進行自由定價，然而，用它來確定收益率的情形還是很多。